Одной из важных и актуальных задач в различных отраслях промышленности и энергетике является повышение эффективности проводимых процессов. Теплообменные аппараты - наиболее распространенные устройства во всех видах и типах энергетических и массообменных установок. Поэтому необходимо стремиться, чтобы теплообменник обеспечивал по возможности наиболее высокие параметры теплообмена. В основу разработки высококачественных компактных теплообменных аппаратов могут быть положены различные решения. Для достижения поставленных целей используют различные средства с помощью как активных, так и пассивных методов, например увеличение скорости потоков теплоносителей, развитие площади теплопередающей поверхности и турбулизацию потоков взаимодействующих сред через разделяющую стенку.
При турбулентном режиме движения перенос теплоты внутри теплоносителя осуществляется в основном путем перемешивания. Весь поток насыщен беспорядочно движущимися вихрями, которые непрерывно возникают и затухают. Одной из причин их возникновения является потеря устойчивости ламинарного течения, сопровождающаяся образованием завихрений, которые затем диффундируют в ядро и, развиваясь, заполняют весь поток. Одновременно с этим, вследствие вязкости теплоносителя, эти вихри постепенно затухают и исчезают. При турбулентности в тонком слое у поверхности, из-за наличия вязкого трения, течение теплоносителя затормаживается и скорость падает до нуля. При этом процесс перемешивания протекает настолько интенсивно, что по сечению ядра потока температура теплоносителя практически постоянна. Резкое изменение температуры наблюдается лишь внутри тонкого слоя у поверхности. При этом одной из основных задач является определение коэффициентов теплоотдачи.
В данной статье рассмотрен приближенный подход определения средних коэффициентов теплоотдачи в каналах с хаотичной насадочной упаковкой. Для этого используется модель пограничного слоя с функцией турбулентной вязкости с учетом затухания турбулентных пульсаций в вязком подслое.
Определение коэффициента теплоотдачи в трубе
Процессы теплоотдачи неразрывно связаны с условиями движения теплоносителя, поэтому для процессов теплоотдачи режим движения рабочей среды имеет очень большое значение, так как им определяется механизм переноса теплоты.
При турбулентном режиме перенос теплоты осуществляется теплопроводностью лишь в тепловом подслое, а внутри турбулентного ядра перенос осуществляется путем интенсивного перемешивания частиц теплоносителя. В этих условиях интенсивность теплоотдачи определяется термическим сопротивлением пристенного подслоя, которое по сравнению с термическим сопротивлением ядра оказывается определяющим.
Так как теплоотдача определяется не только тепловыми, но и гидродинамическими явлениями, то совокупность этих явлений описывается системой дифференциальных уравнений, в которую входят уравнение теплопроводности, уравнение движения и уравнение сплошности. Решение системы дифференциальных уравнений конвективного теплообмена возможно при введении упрощающих предположений. Задача аналитического определения коэффициента теплоотдачи значительно упрощается с использованием моделей пограничного слоя (Прандтля, Кармана и др.), согласно которым силы вязкости играют существенную роль только в пределах вязкого подслоя, а в остальной части потока ими можно пренебречь. Количественное соотношение между трением и теплоотдачей можно найти, воспользовавшись аналогией Рейнольдса и Чилтона – Кольборна. С учетом затухания турбулентных пульсаций в вязком подслое используются модели Ландау – Левича и др.
Сопротивление переносу импульса в турбулентном пограничном слое в одномерной подстановке записывается в виде [3]
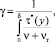(1)
где ν, νт – коэффициенты молекулярной и турбулентной вязкости, м2/с; δ – толщина пограничного слоя; τ* – безразмерный поток импульса; y – поперечная координата пограничного слоя, м.
На основе трехслойной модели турбулентного пограничного слоя, с учетом затухания турбулентных пульсаций, характеристики турбулентного обмена имеют вид [9]
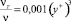, (2)
где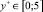 
, (вязкий подслой);
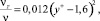(3)
где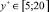 
, (переходная область);
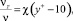(4)
где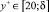 
, (область развития турбулентности),
где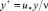 
– безразмерная координата; χ = 0,4.
После интегрирования выражения (1) с функциями (2)–(4) получен коэффициент переноса импульса
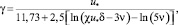(5)
где u* – динамическая скорость (скорость касательного напряжения), м/с.
Для турбулентного пограничного слоя в случае Pr = 1 и градиенте давления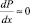 
следует подобие безразмерных профилей скорости и температуры и полная аналогия переноса. В случае Pr ≠ Sc ≠ 1 используется поправка Чилтона – Кольборна, где неоднородность полей учитывается числами Прандтля и Шмидта. Показатели степени этих чисел зависят от гидродинамических условий взаимодействий фаз.
Связь между коэффициентами переноса импульса γ и тепла α имеет вид [3]
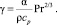(6)
Откуда
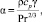(7)
где ρ – плотность среды, кг/м3; cp – удельная теплоемкость среды, Дж/(кг К).
Показатель степени при числе Прандтля α ~ Pr–0,66 следует из закона затухания турбулентных пульсаций в пограничном слое, однако большинство известных экспериментальных данных для пластины и трубы показывают α ~ Pr–0,57.
Используя установленную связь между коэффициентами переноса, на основе применения уравнений (5) и (7), можно записать средний коэффициент теплоотдачи в турбулентном однофазном потоке
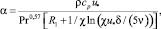(8)
где R1 = 11,7 – безразмерная толщина вязкого подслоя.
Уравнение (8) является достаточно общим и позволяет определять коэффициенты теплоотдачи для различных условий турбулентного движения среды при соответствующих вычислениях его параметров.
С учетом выражения (8) получим безразмерный комплекс Нуссельта для трубы
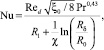(9)
где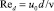 
– число Рейнольдса; u0 – средняя скорость среды в трубе, м/с; d – диаметр трубы, м; ν – кинематическая вязкость среды, м2/с; ξ0 – коэффициент гидравлического сопротивления; R0 = 5 – безразмерная толщина вязкого подслоя в трехслойной модели; 
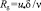– безразмерная толщина пограничного слоя; Pr – число Прандтля. Показатель степени при Pr0,43 принят по экспериментальным данным.
Касательное напряжение или динамическая скорость обычно находится на основе известных коэффициентов трения или сопротивления. Для круглой трубы выражения динамической скорости u* и Rδ в уравнении (9) имеют вид
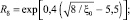(10)
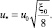(11)
Уравнение (10) следует из логарифмического профиля скорости при y = δ, а (11) – из уравнения баланса сил в трубе.
Коэффициент гидравлического сопротивления ξ0 = f(Red) для трубы запишем по формуле Блазиуса
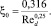(12)
В зависимости от состояния поверхности и характера движения сред число Нуссельта определяется по различным критериальным уравнениям. Для сравнения результатов расчетов числа Нуссельта (Nu = αd/λ) по (9) использовалась известная формула для трубы (при турбулентном режиме движения сред)
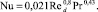(13)
Результаты расчетов по представленным выражениям (9) и (13) даны на рис. 1.
Согласование результатов с расхождением не более 1,5–4 %.
Коэффициент теплоотдачи в канале с хаотичной насадочной упаковкой
Значительно более сложной задачей является определение теоретическим путем коэффициентов теплоотдачи для поверхностей с элементами интенсификации. В настоящее время для этого используются в основном различные полуэмпирические подходы.
Рассмотрим турбулентное течение жидкости в каналах с хаотичной насадочной упаковкой (мелкими насадочными элементами).
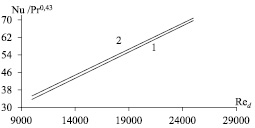
Рис. 1. Зависимость числа Нуссельта от числа Рейнольдса: 1 – расчет по выражению (13); 2 – расчет по выражению (9)
Динамическая скорость в каналах с хаотичной насадочной упаковкой получена в виде [4, 5, 7]
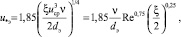(14)
где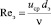 
– число Рейнольдса для насадки; uср – скорость потока в насадке, м/с; dэ – эквивалентный диаметр насадки, м; ξ – коэффициент сопротивления насадочного слоя.
С учетом выражений (8) и (14) запишем число Нуссельта для канала с хаотичной насадочной упаковкой (слоем) учитывая, что Nuэ ~ Pr0,333
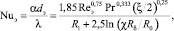(15)
где параметры уравнения имеют вид
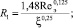
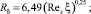
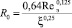[7].
Данные параметры определены на основе отношения потоков импульса в невозмущенном и возмущенном пограничном слое.
Для проверки адекватности полученного выражения числа Нуссельта (15) произведем сравнение по следующим известным уравнениям (40 < Reэ < 104) [4, 7]:
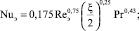(16)
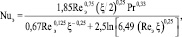(17)
уравнение Гильденблата (для колец Рашига и Палля) [8]
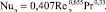(18)
Следует отметить, что число Reэ вычисляется через действительную скорость потока в насадке, которая связана с фиктивной (без насадки) выражением uср = u0/εсв, м/с.
Результаты расчетов
Рассмотрим применение выражений для расчета числа Нуссельта в канале с хаотичной насадочной упаковкой.
Для колец Рашига коэффициент гидравлического сопротивления имеет вид (при Reэ > 50) [8]
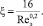(19)
На рис. 2 представлены расчетные значения чисел Нуссельта от числа Рейнольдса в канале с хаотичной насадочной упаковкой. Расчет проводился с использованием выражений (15)–(18).
На основании представленных результатов можно сделать вывод, что полученное выражение (15) для канала, заполненного хаотичной насадочной упаковкой, удовлетворительно согласуется с известными выражениями. Расхождение результатов в пределах 13–15 %.
На рис. 3 представлены экспериментальные данные по числу Нуссельта при теплоотдаче от нагретого воздуха в нерегулярном насадочном слое из цилиндров и параллепипидов.
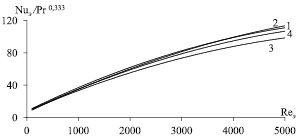
Рис. 2. Зависимость числа Нуссельта от числа Рейнольдса: 1 – расчет по выражению (15); 2 – (16); 3 – (17); 4 – (18)
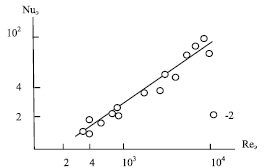
Рис. 3. Теплоотдача в слоях насадочных элементов: 1 – расчет по уравнению (15); 2 – опытные данные [1]
Приведенные выражения рекомендуются для практических расчетов.
Выводы
Полученные результаты по моделированию интенсифицированного теплообмена в каналах с хаотичной упаковкой, по сравнению с гладкими (пустотелыми) каналами, показывают значительное повышение числа Nud (в 20–40 раз и более) [6].
Однако это сопровождается и повышением гидравлического сопротивления. Наиболее эффективным способом такой интенсификации является турбулизация среды за счет хаотичных насадок при ламинарном движении. Полученное выражение (15) может применяться в расчете интенсифицированного теплообмена.