Исследование температурных полей при течении жидкости и газа по трубам является актуальной задачей для транспорта теплоносителей по трубопроводам и продуктопроводам и имеет большое значение для прогноза температуры в стволах нефтяных скважин. С одной стороны, расчеты температурных полей в скважинах необходимы для определения возможности отложения парафина на стенках скважины; с другой стороны, это задача термокаротажа, которая широко используется на практике для исследования скважин и пластов, поэтому изучение температурных полей в скважине давно интересует исследователей. Нестационарные температурные поля в стволах скважины и окружающей среде оказывают взаимное влияние друг на друга. Естественным граничным условием, определяющими это взаимодействие, является равенство температуры и тепловых потоков на стенке труб. Задачу в такой постановке называют сопряженной [7]. Э.Б. Чекалюк предложил интегральный метод для учета теплообмена потока с окружающими породами, где тепловой поток задавался в виде свертки. В рамках этого же подхода выполнены исследования А.Н. Саламатина [2]. К обсуждаемой проблеме обращались и другие исследователи [3, 10], рассматривающие задачу только для средней температуры в скважине. Между тем использование термических исследований в практике разработки нефтегазовых месторождений привело к необходимости расчета радиальных зависимостей температуры. Попытка построения теории таких тепловых процессов в скважине на основе асимптотических методов [9] предпринята в [6], где удалось построить решение задачи о температурном поле в скважине в пространстве Лапласа – Карсона, оригинал которых построен только для малых и больших времен. В данной работе для инверсии преобразований использован численный метод [8], который позволяет строить оригинал для любого времени.
Физическая постановка задачи
Предполагается, что окружающая среда является однородной и анизотропной, температура отдаленных участков пород изменяется по линейному закону с глубиной, рассматривается область глубин, куда не проникают сезонные колебания температуры на поверхности земли. Задача о температурном поле в трубе имеет осевую симметрию, поэтому выбрана цилиндрическая система координат. Из условия симметрии следует, что производная по радиальной координате на оси zd цилиндрической системы координат, направленной вверх, в центре скважины обращается в ноль. На рисунке представлена геометрия задачи о температурном поле жидкости, текущей в трубе радиуса r0.
Цилиндрическая система координат ориентирована таким образом, что ось zd направлена по оси трубы. Труба окружена анизотропным массивом с теплопроводностями λr1 и λz1 в соответствии с направлениями осей. Поле скоростей жидкости в трубе имеет только одну отличную от нуля составляющую – в направлении оси zd 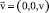 . Жидкость вследствие своего движения также приобретает фиктивные анизотропные свойства, связанные с воздействием турбулентности (λr и λz – соответствующие осям теплопроводности жидкости).
. Жидкость вследствие своего движения также приобретает фиктивные анизотропные свойства, связанные с воздействием турбулентности (λr и λz – соответствующие осям теплопроводности жидкости).
Математическая постановка задачи
Система безразмерных уравнений в предположении осевой симметрии включает уравнение теплопроводности в окружающем скважину массиве:
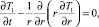
r > 1, t > 0, z > 0, (1)
уравнение конвективной теплопроводности флюида (в общем случае – многофазного) с источниками в скважине:
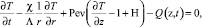
r < 1, t > 0, z > 0. (2)
На границе скважины и окружающего массива задаются условия равенства температур
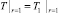 (3)
(3)
и тепловых потоков
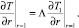 (4)
(4)
Начальные условия соответствуют естественной, невозмущенной
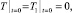 (5)
(5)
которая совпадает с температурой в удаленных от стенки скважины точках окружающего массива
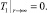 (6)
(6)
В точке z = 0 температура изменяется по заданному закону
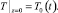 (7)
(7)
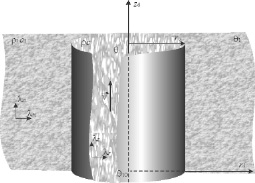
Рис. 1. Геометрия задачи
В уравнении (2) 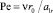 – конвективный параметр,
– конвективный параметр,
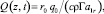
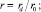
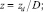
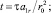
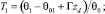
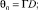
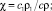
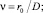
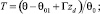
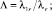
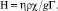
В такой постановке построить точное решение задачи достаточно трудно. Для получения приближенных решений использован асимптотический метод [5, 6, 9].
В задаче (1)–(7) формальной заменой L на ε·L введен произвольный параметр e асимптотического разложения. Решение задачи ищется в виде ряда
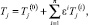 (8)
(8)
где j = пробел или 1 – номер области; i – порядковый номер приближения.
Подставив (8) в задачу (1)–(7), выделяются задачи для коэффициентов ряда. Показано, что нулевое приближение позволяет получить новые способы расчета средней по сечению температуры.
Решение уравнения для нулевого коэффициента в пространстве Лапласа – Карсона имеет вид
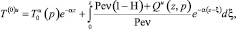 r < 1, z > 0, (9)
r < 1, z > 0, (9)
где 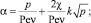
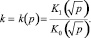
Задача для первых коэффициентов асимптотического ряда представится следующим образом:
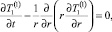 r > 1, t > 0, z > 0; (10)
r > 1, t > 0, z > 0; (10)
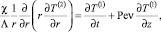 r < 1, t > 0, z > 0; (11)
r < 1, t > 0, z > 0; (11)
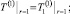 (12)
(12)
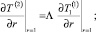 (13)
(13)
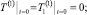 (14)
(14)
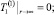 (15)
(15)
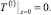 (16)
(16)
Во-первых, в уравнениях коэффициенты асимптотического ряда взаимосвязаны, поэтому нужна специальная процедура их разделения; во-вторых, задача с указанными начальными и граничными условиями имеет лишь тривиальное решение, что приводит к необходимости замены граничных условий. Указанные процедуры подробно описаны в [10].
Искомое решение для первого коэффициента асимптотического решения примет вид
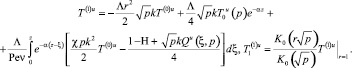 (17)
(17)
Из приведенных решений видно, что нулевое приближение определяет средние значения температуры в скважине, а радиальные зависимости описываются первым приближением.
Как известно, оригиналы функций строятся либо непосредственным интегрированием в комплексной плоскости, либо с помощью различных специальных справочников, например, таких как [1]. Существует достаточно много классов задач, в которых применение метода интегральных преобразований ограничено возможностью построения функции по ее изображению. Рассматриваемая задача является именно такой. Это привело к ограничению исследований и рассмотрению лишь крайних случаев для «больших» (t → ∞) и «малых» (t → 0) времен [6, 4] и породило новую проблему: в каком диапазоне времени можно пользоваться решением, полученным для малых, в каком – для больших времен? Многие исследователи связывают решение указанных выше проблем с численными методами.
Численное обращение обратного преобразования Лапласа и Лапласа – Карсона изучается довольно давно. В [8] определена точность численного обращения некоторых функций с помощью различных алгоритмов и показано, что метод с использованием гауссовских квадратур может инвертировать лапласовские преобразования функций с неоднородностями и особенностями, и результаты имеют более высокую точность, чем в случае применения других методов. Поэтому в работе для численной инверсии преобразования Лапласа – Карсона (9), (17) использован метод, основанный на гауссовских квадратурах.
Результаты расчетов
На рис. 2, 3 представлены графики зависимости температуры в скважине от времени, по формулам, полученным из (9) для малых и больших времен, а также при численной инверсии в нулевом приближении для случая постоянных градиентов (рис. 2) и первом приближении для основной задачи термокаротажа (рис. 3).
Расчеты проведены при следующих значениях параметров: глубина скважины D = 2000 м; радиус скважины r0 = 0,1 м; естественный градиент температуры Земли Г = 0,02 K/м; удельные теплоемкости, плотности, коэффициенты теплопроводности окружающих скважину пород и нефти соответственно:
c1 = 950 Дж/(К∙кг), c = 2000 Дж/(К∙кг);
ρ1 = 2000 кг/м³; ρ = 800 кг/м³;
λ1r = 0,67 Вт/(м·К); λ = 0,15 Вт/(м∙К);
z = 0,1; r = 0,1.
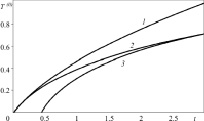
Рис. 2. Зависимость температуры в скважине от времени в нулевом приближении в случае постоянных вертикальных градиентов внутри скважины: 1 – построена по формуле, полученной для малых времен; 2 – используя численное обращение; 3 – для больших времен
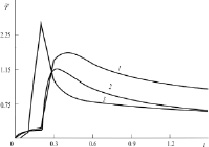
Рис. 3. Зависимость относительной температуры от времени: 1 – по аналитической формуле, после численного обращения; 2 – для малых времен; 3 – для больших времен
Сравнение графиков позволяет заключить, что малым временам соответствует 0 < t < 0,2, а большим t > 2 (t – безразмерное время, t = 1 соответствует 24,35 мин); в отличие от предыдущих работ, результаты численного обращения позволяют определить значение температуры в любой момент времени. Заметим также, что при 0,2 < t < 2 применение в расчетах формул для малых или больших времен приводит к ошибкам и относительная погрешность составляет 25 %.
С применением численного обращения преобразований Лапласа – Карсона построены зависимости температуры от расстояния до оси скважины, как в скважине, так и окружающем массиве (рис. 4). Перепад температуры между центром и стенкой скважины составляет около 15 %, что может служить основой технологии радиального каротажа скважины.
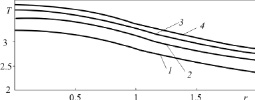
Рис. 4. Радиальные профили первого приближения температуры для нефти при различных временах: 1 при t = 1, 2 – t = 2, 3 – t = 3, 4 – t = 4
Список обозначений
Латинские:
a1r – коэффициент температуропроводности окружающей среды в радиальном направлении, м²/с;
c, c1 – удельная теплоемкость флюида и окружающей среды соответственно, Дж/(К·кг);
D – глубина скважины, м;
g – ускорение свободного падения, м/с²;
H – толщина пласта, м;
k – отношение функций Бесселя K1(p) и K0(p);
p – параметр преобразования Лапласа – Карсона;
Pe – аналог параметра Пекле;
q – плотность источников тепла, Вт/м³;
rd, r – соответственно размерная и безразмерная радиальная координата цилиндрической системы координат, м;
r0 – внутренний радиус трубы, м;
t – безразмерное время, с;
T, T1 – безразмерное температурное поле флюида и окружающей среды соответственно;
T0 – безразмерный температурный сигнал пласта;
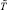 – безразмерный радиальный профиль температуры внутри скважины;
– безразмерный радиальный профиль температуры внутри скважины;
v0 – средняя по сечению трубы скорость, м/c;
zd, z0 – соответственно размерная и безразмерная вертикальная координата цилиндрической системы координат, м.
Греческие:
Γ – геотермический градиент Земли, К/м;
ε – параметр асимптотического разложения;
η – адиабатический коэффициент, К/Па;
θ, θ1 – температурное поле флюида и окружающей среды соответственно, К;
θ0 – температурный сигнал пласта, К;
θ01 – естественная невозмущенная температура Земли в точке zd = 0, К;
 – радиальный профиль температуры внутри скважины, К;
– радиальный профиль температуры внутри скважины, К;
λ, λ1 – коэффициент теплопроводности флюида и окружающей среды соответственно, Вт/(м·К);
λr, λz – коэффициент теплопроводности флюида в радиальном и вертикальном направлении соответственно, Вт/(м·К);
λ1r, λ1z – коэффициент теплопроводности окружающей среды в радиальном и вертикальном направлении соответственно, Вт/(м·К);
Λ – отношение теплопроводностей в радиальном направлении окружающей среды и флюида;
ν – отношение радиуса трубы к глубине скважины;
ξ – переменная интегрирования;
ρ, ρ1 – плотность флюида и окружающей среды соответственно, кг/м³;
τ – размерное время, с;
χ – отношение объемных теплоемкостей окружающей среды и флюида.
Рецензенты:
Шулаев Н.С., д.т.н., профессор, заведующий кафедрой информатики, математики и физики, филиал, ФГБОУ ВПО УГНТУ, г. Стерлитамак;
Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой прикладной информатики и программирования, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.



