Известно, что основным техническим показателем, характеризующим резонансные свойства древесины, является акустическая константа K, предложенная акад. Н.Н. Андреевым, м4/(кг·с):

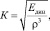(1)

где Е_дин – динамический модуль упругости, Па; ρ – плотность, кг/м3.

Следовательно, для ее определения необходимо знать значение плотности и модуля упругости древесины.

Плотность является косвенным показателем (отношение массы к объему). Для измерения плотности древесины существуют десятки методов, часть которых, включая стандартные и новейшие, подробно изложена в работе О.И. Полубояринова [1, 5]. Выбор того или иного метода связан в основном с производственными условиями и возможностями целевого отбора резонансного сырья (на корню, в круглых или пиленых лесоматериалах, заготовках и т.д.).

Наиболее практичным (производительным) для отбора резонансной древесины в круглых лесоматериалах, тем более на корню, является способ, основанный на определении плотности путем погружения образцов нестандартной формы и размеров в жидкость с дальнейшим выявлением выталкивающей силы [5]; при этом отпадает необходимость не только в изготовлении стандартных образцов, но и не требуется их специальная калибровка в сушильных камерах.

Модуль упругости можно определить путем измерения упругих деформаций при статических испытаниях материала различными методами [4, 6].

В соответствии с ГОСТ 16483.9 можно определить статический модуль упругости через величину прогиба образца в форме прямоугольного бруска сечением 20×20 мм и длиной вдоль волокон 300 мм [3]. Испытание проводят при действии изгибающего усилия перпендикулярно радиальной поверхности образца. Образец с закрепленным на нем прибором для измерения прогиба нагружают по схеме (рис. 1).

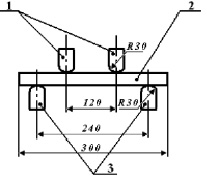
Рис. 1. Схема определения модуля упругости по ГОСТ 16483.9: 1 – нажимные ножи; 2 – образец для испытаний; 3 – опоры

Модуль упругости древесины при кондиционировании образцов (EW) в МПа вычисляют по формуле

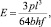(2)

где l – расстояние между опорами; мм; p – нагрузка, равная разности между верхним и нижним пределами нагружения, Н; b – ширина образца, мм; h – высота образца, мм; f – прогиб образца в зоне чистого изгиба, равный разности между средними арифметическими результатами измерения прогиба при верхнем и нижнем пределах нагружения, мм. При этом может применяться многократная нагрузка и разгрузка.

Для такого материала, как древесина, обладающего свойством пластичности, особенно в раннем возрасте, характерно явление остаточной деформации.

С целью исключения данного фактора следует использовать динамический модуль упругости. В ряде случаев динамический модуль упругости определяется быстрее и проще, чем статический. К тому же использование динамического модуля упругости для характеристики упругих свойств дает больше возможности для исследования влияния различных факторов, в том числе влажности и температуры, поскольку образцы древесины при испытаниях не разрушаются, что дает возможность использовать их для других испытаний, подвергать многократному увлажнению и высушиванию.

Наиболее простым и удобным является определение динамического модуля упругости резонансным методом по собственной (резонансной) частоте образца. Данным методом исследовались образцы зрелой древесины стандартной формы и размеров, а также были проведены исследования на кернах. Но для изучения резонансных свойств древесины в раннем возрасте необходимо проводить испытания на боковых побегах. В связи с этим возникает необходимость расширить исследования резонансных свойств древесины, определив значение динамического модуля упругости древесины резонансным методом через собственную частоту образца [7].

Динамический модуль упругости образцов предлагается находить по частоте собственных изгибных или продольных колебаний.

Суть метода заключается в выявлении собственной (резонансной) частоты образца f при пропускании через образец детерминированного звукового сигнала с повышающейся частотой и определении Ед с учетом его рабочей длины l, диаметра d и объемного веса γ, а также константы K по формуле (1).

Структурная схема принципа работы метода представлена на рис. 2. Устройство представляет собой систему из электромагнитного вибратора (3), возбуждающего колебания исследуемого образца (5) с помощью «башмачка» (6) из мягкого железа и электромагнитного датчика (4), регистрирующего амплитуду и частоту колебаний образца. С выхода звуковой платы (2.2) гармонический сигнал по соединительному кабелю подаётся на вибратор (3). Сигнал с датчика поступает на вход звуковой платы компьютера (2.1).

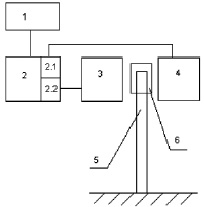
Рис. 2. Структурная схема метода: 1 – монитор; 2 – компьютер, включающий: 2.1 – вход звуковой платы, 2.2 – выход звуковой платы; 3 – вибратор типа ТК-67-Н; 4 – датчик типа ТК67-Н; 5 – образец; 6 – ферромагнитный «колпачок»

Динамический модуль упругости Eдин (кг/см2) находится по следующей формуле:

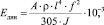(3)

где А – площадь поперечного сечения, см2; ρ – плотность, г/см3; l – свободная длина стержня, см; f – частота колебаний, Гц; J – момент инерции поперечного сечения, см4.

А∙ρ∙L = m; (4)

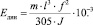(5)

Принимая во внимание, что теоретические основы колебаний упругих тел применялись к древесине, материалу анизотропному и неоднородному, возможность использования уравнения (15) потребовала детальной проверки. В частности, необходимо было установить степень влияния различных факторов, определить соотношение между статическими и динамическими модулями упругости. Исследования ученых доказали адекватность и практическую применимость формулы (4), а также отсутствие значимой разницы между статическим и динамическим модулями упругости у древесины ели [4, 8].

Для получения более точных, близких к истинному значению, показателей резонансной частоты и динамического модуля упругости древесины на примере образцов с консольным типом крепления нужно учесть влияние массы колпачка, который устанавливается на свободный конец образца для создания колебаний исследуемого черенка. С учетом этих дополнений истинная резонансная частота будет определяться по формуле

f_ист = f_рез∙(1 + ∆m/m), (6)

где ∆m – масса «башмачка», кг; m – масса рабочей части образца, кг.

Таким образом, более достоверное, истинное значение динамического модуля упругости образца круглого сечения будет определяться по следующей расчетной формуле:

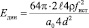(H/м2), (7)

где d – средний диаметр образца, м.

Момент инерции сечения образца с колпачком Jсеч (см4) вычислим по формуле

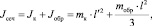(8)

где J_к – момент инерции сечения колпачка, см4; J_обр – момент инерции сечения образца, см4; l′ – длина колпачка, см.

Объединяем формулы (4) и (5) и выразим Eдин (кг/см2) по формуле

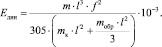(9)

Осуществим перевод единиц измерения Eдин, находимого по формуле (6), из кг/см2 в Па

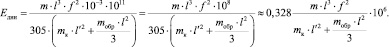(10)

Модуль упругости образцов с влажностью, отличающейся от 12 % более чем на 1 %, в пределах от 8 до 20 %, пересчитываем к влажности 12 % с точностью до 25 МПа по формуле

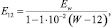(11)

где 1∙10–2 – поправочный коэффициент на влажность для всех пород древесины; W – влажность образцов в момент испытания, %.

Модуль упругости образцов с влажностью, равной или больше предела насыщения клеточных стенок, пересчитываем к влажности 12 % с точностью до 25 МПа по формуле

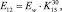(12)

где 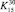– пересчетный коэффициент при влажности 30 %, равный 1,25 для хвойных пород.

Находим акустическую константу K (м4/(кг·с)) из формул (1) и (10):

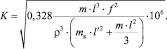(13)

При детальном изучении процесса определения резонансной частоты требуется получить максимально точное описание зависимости отклика от варьируемых параметров. В таком случае наиболее целесообразно построение уравнения регрессии с использованием планов второго порядка. Этим целям удовлетворяет В-план.

Переменными факторами плана являются: х1 – рабочая длина образца lраб; х2 – диаметр образца d; х3 – усилие зажима образца в устройстве, p. Пределы варьирования факторов и полученные экспериментальные результаты приведены в таблице.

За постоянные факторы приняты: порода и влажность древесины, масса колпачка.

Выходной параметр Y – собственная (резонансная) частота образца, являющаяся функцией от переменных факторов

Y = f(х1, х2, х3). (14)

Была получена регрессионная модель в виде следующего уравнения:

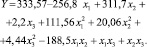(15)

Данное уравнение регрессии характеризует зависимость собственной (резонансной) частоты древесины fрез при поперечном колебании от диаметра образца, рабочей длины и усилия зажима. Анализ математической модели показал, что все предложенные коэффициенты регрессионного уравнения значимы и модель пригодна к применению, т.к. адекватно описывает реальный процесс.

Результаты экспериментальных исследований при варьировании переменных факторов

Рецензенты:

Торопов А.С., д.т.н., профессор кафедры деревообрабатывающих производств лесопромышленного факультета, ФГБОУ ВПО ПГТУ, г. Йошкар-Ола;

Федюков В.И., д.т.н., профессор, зав. кафедрой «Стандартизация, сертификация, товароведение», ФГБОУ ВПО ПГТУ, г. Йошкар-Ола.

Работа поступила в редакцию 16.02.2015.