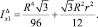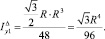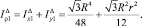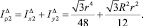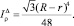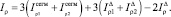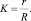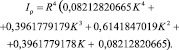Razumov M.S. 1
Gladyshkin A.O. 1
Zinovkin A.A. 1
Pykhtin A.I. 1
Sidorova M.A. 1
1 Southwest State University
The paper deals with a method for determining the basic geometrical characteristics of the section (square, axial and polar moment of inertia) as a Reuleaux triangle. The article describes the main advantages and disadvantages of this type of compounds in comparison with the currently used conventional connections (keyed, splined, multifaceted correct form). It also provides a detailed calculation of axial moment of inertia of circular segments. With the help of these curves it is possible to determine with a high degree of accuracy normal and shear stresses arising in connection with the profile of torque transmission. These dependencies can be used for automated connection strength calculations for the third theory of strength that will reduce the time to design and technological preparation of manufacture of products containing in their joint design based on Reuleaux triangle.
polar moment of inertia
axial moment of inertia
the profile connection
normal tension
shear stress
1. Avtomatizacija prochnostnogo rascheta mnogogrannyh valov na kruchenie (Automation strength calculation polyhedral shaft torsional) V.N. Kassikhin, M.S. Razumov, A.O. Gladyshkin, N.E. Bykovskaya // Proceedings of the Southwestern State University: Engineering and technology. 2012. no. 2–1. рp. 179–181.
2. Avtomatizacija tehnologicheskoj podgotovki proizvodstva profil’nyh valov (Automation of technological preparation of production of profile shaft). S.G. Emeljanov, A.O. Gladyshkin, M.S. Razumov, S.F. Jacun. News of SouthWest state university. 2012. no. 1–1. рp. 164–168.
3. Avtomatizirovannaja sistema dlja realizacii graficheskogo reshenija stepennyh funkcij (Automated system for implementing the graphical solution of power functions) A.I. Barbotko, M.S. Razumov, P.A. Ponkratov [et al.] Proceedings of the Southwestern State University. 2013. no. 1 (46). рp. 90–94.
4. Analiticheskoe opredelenie kinematicheskih perednego i zadnego uglov instrumenta pri formirovanii grannyh poverhnostej s peremennym profilem planetarnym tocheniem (Analytical determination of kinematic front and rear corners of the tool in forming faceted surfaces with variable profile planetary turning) M.S. Razumov, A.N. Grechukhin, A.I. Pykhtin [et al.] Basic Research. 2014. no. 5–4. рp. 711–715.
5. Barbotko, A.I. Matematicheskaj statistika v mashinostroenii (Mathematical statistics in engineering): studies. Manual A.I. Barbotko, A.O. Gladyshkin; Kursk. state. tehn. Univ. Kursk. 2006. 320 p .: tab. 177, ill. 46
6. Barbotko, A.I. Obrabotka mnogogrannikov s chetnym chislom storon na tokarnom stanke (Processing polyhedra with an even number of sides on a lathe) A.I. Barbotko, M.S. Razumov Bulletin of Engineering. 2010. no. 1. рp. 46–48.
7. Barbotko, A.I. Osnovy matematicheakogo modelirovanija (Fundamentals of the theory of mathematical modeling): a tutorial A.I. Barbotko, A.O. Gladyshkin. Art. Oskol: TNT Ltd. , 2008. 212 p.
8. Grechukhin, A.N. Eksperimental’noe opredelenie minimal’nogo znachenija zadnego ugla instrumenta pri obrabotke profil’noy chasti pruzhin zheleznodorozhnogo transporta posredstvom planetarnogo mechanozma (Experimental determination of the minimum value of the clearance angle of the tool during machining of the airfoil spring rail transport through the planetary gear) A.N. Grechukhin, M.S. Razumov, S.A. Chevychelov Fundamental problems of engineering and technology. 2013. no. 3–2. рр. 50–55.
9. Opredelenie pogreshnosti formy pri obrabotke mnogogrannikov na tokarnom stanke (Determination of errors in the processing of forms polyhedra on a lathe) A.I. Barbotko, M.S. Razumov, A.O. Gladyshkin [et al.] Proceedings of the South-Western State university .– 2011. no. 3 (36). рр. 130–134.
10. Ponkratov P.A.Technologija obrabotki profil’nyh valov chashechnymi dolbjakami (Processing technology core shafts cup cutter) P.A. Ponkratov, A.I. Barbotko, M.S. Razumov // Engineering from theory to practice International scientific and technical conference. 2013. no. 17–1. рp. 75–79.
11. Proverochnyj raschet zagotovok na zhestkost’ v processe formoobrazovaniy grannyh poverhnostey s peremennym profilem planetarnym tocheniem (Calculation check blanks on the stiffness in the formation of faceted surfaces with variable profile planetary turning) A.O. Gladyshkin, A.N. Grechukhin, M.S. Razumov [et al.] Directory. Engineering magazine with the application. 2014. no. 4 (205). рр. 13–16.
12. Proektirovanie profilja dolbezhnogo instrumenta dlja formirovanija profil’nyh otverstij (Design Profile slotting tool for the formation of core holes) P.A. Ponkratov, A.I. Barbotko, M.S. Razumov [et al.] Modern problems of science and education: electronic scientific journal. 2013. no. 5. рр. 113.
13. Razumov M.S. Kombinirovannyj sposob obrabotki profil’nyh valov posredstvom planetarnogo mehanizma (Combined method of processing core shaft by the planetary gear) M.S. Razumov Proceedings of the South-Western State University. Series: Engineering and technology. 2012. no. 2–1. рp. 83–86.
14. Razumov, M.S. Povyshenie proizvoditel’nosti formoobrazovanija mnogogrannyh naruzhnyh poverhnostej posredstvom planetarnogo mehanizma. (Increase of productivity of a shaping of many-sided external surfaces by means of the planetary mechanism): Abstract of the thesis of Candidate of Technical Sciences. M.S. Razumov Kursk, 2011. 18 р.
Использование в промышленности (машино-, автомобиле-, приборостроении) профильных валов вместо шлицевых и шпоночных является перспективным в плане обеспечения достаточной надежности тяжелонагруженных соединений [1, 2, 3]. В настоящее время существует несколько способ по реализации формообразования данного вида валов, однако в условиях автоматизации конструкторско-технологической подготовки производства многие вопросы, связанные с прочностными расчетами [6, 8, 10, 13, 14] очень актуальны.
Для решения данной проблемы было предложено производить оценку прочности соединения исходя из расчета на изгиб с кручением [5, 9, 11, 12]. Требуется с большой точностью определить значение осевых и полярного моментов инерции поперечного сечения [4, 7] (рис. 1).
Расчет моментопередающих соединений на кручение в основном заключается в определении максимального касательного напряжения в поперечном сечении. Основная расчетная формула для определения тангенциального напряжения в точке с координатой y ‒
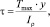
где Тmax – максимальный крутящий момент, передаваемый валом; Iρ – полярный момент инерции сечения.
Когда сечение имеет простую форму, определение Iρ не составляет никаких сложностей. В общем виде его можно представить в виде суммы двух осевых моментов инерции
Iρ = IХс + IYс. (1)
Моментопередающее соединение имеет в поперечном сечении достаточно сложный профиль.
Высота центрального треугольника равна
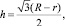 (2)
(2)
где R ‒ радиус описанных окружностей из вершин центрального треугольника.
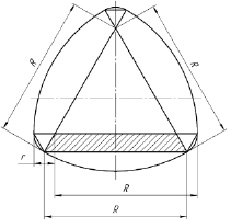
Рис. 1. Плоское сечение моментопередающего вала
Расстояние от оси Х1 до центральной Хс определяется по формуле
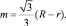
Полярный момент инерции большего кругового сегмента относительно Хс:
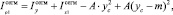 (3)
(3)
где A – площадь кругового сегмента.
Теперь определим осевые моменты инерции IX1, Iy и площадь кругового сегмента (рис. 2 и 3).
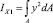 и
и 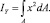
При вычислении IX1 элементарная площадка расположена на расстоянии y = R∙sin α. Соответственно, dy = Rcos αdα. Угол может изменяться в пределах 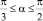 . Площадь кругового сегмента равна
. Площадь кругового сегмента равна
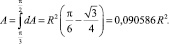 (4)
(4)
Момент инерции относительно оси IX1 равен
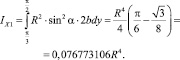 (5)
(5)
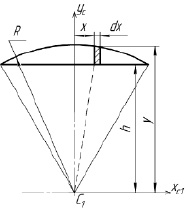
Рис. 2. Определение осевого момента инерции кругового сегмента относительно оси YC
Теперь вычислим Iy
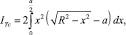
где x = Rcos t – расстояние от оси Y до элементарной площадки.
Удобнее всего этот интеграл брать в параметрическом виде. Введем параметр t следующим образом:
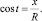
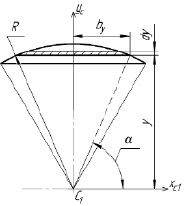
Рис. 3. Определение осевого момента инерции кругового сегмента относительно оси XC1
Соответственно
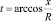 ,
, 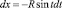 .
.
Следовательно, у нас поменяются пределы интегрирования:
при x1 = 0, 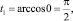
при 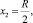
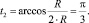
В итоге получим
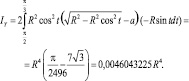 (6)
(6)
Статический момент кругового сегмента относительно оси X1 равен
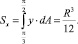 (7)
(7)
Координата центра тяжести определяется по формуле
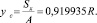 (8)
(8)
Окончательно, подставляя (4), (5), (6) и (8) в (3), получаем полярный момент инерции большего кругового сегмента:

Полярный момент инерции меньшего кругового сегмента относительно Хс:
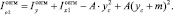
Все переменные находятся аналогично. Следовательно, полярный момент малого кругового сегмента

Вычислим полярные моменты малого и большого треугольника относительно Х.
Момент инерции относительно оси Х большого треугольника
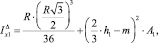
где 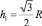 – высота треугольника;
– высота треугольника; 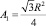 – площадь треугольника.
– площадь треугольника.
Следовательно,
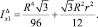
Момент инерции относительно оси Y большого треугольника
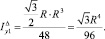
Полярный момент большего треугольника равен
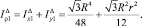
Аналогично находится полярный момент малого треугольника:
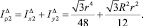
Полярный момент центрального треугольника равен
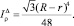
Окончательный полярный момент фигуры вычисляется по формуле
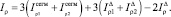
Введём новую переменную
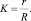
Тогда
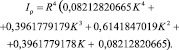
С помощью полученных зависимостей становится возможным определить с высокой степенью точности нормальные и касательные напряжения, возникающие в профильном соединении при передаче крутящего момента. Указанные зависимости могут быть использованы при автоматизированном прочностном расчете соединения по 3-ей теории прочности, что позволит сократить время на конструкторско-технологическую подготовку производства изделий, содержащих в своей конструкции соединения на базе треугольника Рёло.
Работа выполнена в рамках гранта Президента РФ по государственной поддержке молодых российских ученых ‒ кандидатов наук МК-2653.2014.8.
Рецензенты:
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск;
Яцун С.Ф., д.т.н., профессор, заведующий кафедрой механики, мехатроники и робототехники, ЮЗГУ, г. Курск.
Работа поступила в редакцию 16.02.2015.
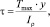
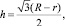 (2)
(2)

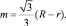
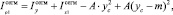 (3)
(3)
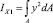 и
и 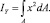
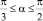 . Площадь кругового сегмента равна
. Площадь кругового сегмента равна
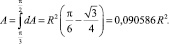 (4)
(4)
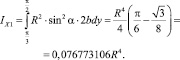 (5)
(5)

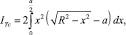
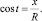

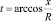 ,
, 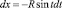 .
.
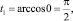
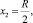
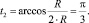
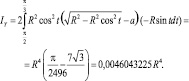 (6)
(6)
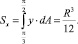 (7)
(7)
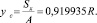 (8)
(8)

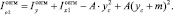

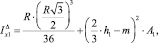
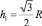 – высота треугольника;
– высота треугольника; 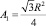 – площадь треугольника.
– площадь треугольника.