Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Разумов М.С. 1 Гладышкин А.О. 1 Зиновкин А.А. 1 Пыхтин А.И. 1 Сидорова М.А. 1

---

1 ФГБОУ ВПО «Юго-Западный государственный университет»

В работе рассматривается способ определения основных геометрических характеристик сечения (площадь, осевые и полярный моменты инерции) в виде треугольника Рёло. В статье описываются основные достоинства и недостатки соединений такого вида в сравнении с использующимися на данный момент общепринятыми соединениями (шпоночные, шлицевый, многогранной правильной формы). Также приводится подробный расчет осевых моментов инерции круговых сегментов. С помощью полученных зависимостей становится возможным определить с высокой степенью точности нормальные и касательные напряжения, возникающие в профильном соединении при передаче крутящего момента. Указанные зависимости могут быть использованы при автоматизированном прочностном расчете соединения по 3-й теории прочности, что позволит сократить время на конструкторско-технологическую подготовку производства изделий, содержащих в своей конструкции соединения на базе треугольника Рёло.

Статья в формате PDF

763 KB

полярный момент инерции

осевой момент инерции

профильное соединение

нормальное напряжение

касательное напряжение

1. Автоматизация прочностного расчета многогранных валов на кручение / В.Н. Кассихин, М.С. Разумов, А.О. Гладышкин, Н.Е Быковская // Известия Юго-Западного государственного университета. Серия: Техника и технологии. – 2012. – № 2–1. – С. 179–181.

2. Автоматизация технологической подготовки производства профильных валов / С.Г. Емельянов, А.О. Гладышкин, М.С. Разумов, С.Ф. Яцун // Известия Юго-Западного государственного университета. – 2012. – № 1–1. – С. 164–168.

3. Автоматизированная система для реализации графического решения степенных функций / А.И. Барботько, М.С. Разумов, П.А. Понкратов и др. // Известия Юго-Западного государственного университета. – 2013. – № 1 (46). – С. 90–94.

4. Аналитическое определение кинематических переднего и заднего углов инструмента при формообразовании гранных поверхностей с переменным профилем планетарным точением / М.С. Разумов, А.Н. Гречухин, А.И. Пыхтин и др. // Фундаментальные исследования. – 2014. – № 5–4. – С. 711–715.

5. Барботько А.И. Математическая статистика в машиностроении: учеб. пособие / А.И. Барботько, А.О. Гладышкин; Курск. гос. техн. ун-т. Курск. – 2006. 320 с.: табл. 177, ил. 46.

6. Барботько, А.И. Обработка многогранников с чётным числом сторон на токарном станке / А.И. Барботько, М.С. Разумов // Вестник машиностроения. – 2010. – № 1. – С. 46–48.

7. Барботько А.И. Основы теории математического моделирования: учебное пособие / А.И. Барботько, А.О. Гладышкин. – Ст. Оскол: ООО ТНТ, 2008. – 212 с.

8. Гречухин А.Н. Экспериментальное определение минимального значения заднего угла инструмента при обработке профильной части пружин железнодорожного транспорта посредством планетарного механизма / А.Н. Гречухин, М.С. Разумов, С.А. Чевычелов // Фундаментальные проблемы техники и технологии. – 2013. – № 3–2. – С. 50–55.

9. Определение погрешности формы при обработке многогранников на токарном станке / А.И. Барботько, М.С. Разумов, А.О. Гладышкин и др. // Известия Юго-Западного государственного университета. – 2011. – № 3 (36). – С. 130–134.

10. Понкратов П.А. Технология обработки профильных валов чашечными долбяками / П.А. Понкратов, А.И. Барботько, М.С. Разумов // «Технические науки – от теории к практике» – материалы Международной научно-технической конференции. – 2013. – № 17–1. – С. 75–79.

11. Проверочный расчет заготовок на жесткость в процессе формообразования гранных поверхностей с переменным профилем планетарным точением / А.О. Гладышкин, А.Н. Гречухин, М.С. Разумов и др. // Справочник. Инженерный журнал с приложением. – 2014.– № 4 (205). – С. 13–16.

12. Проектирование профиля долбежного инструмента для формирования профильных отверстий / П.А. Понкратов, А.И. Барботько, М.С. Разумов и др. // Современные проблемы науки и образования: электронный научный журнал. – 2013. – № 5. – С. 113.

13. Разумов М.С. Комбинированный способ обработки профильных валов посредством планетарного механизма // Известия Юго-Западного государственного университета. Серия: Техника и технологии. – 2012. – № 2–1. – С. 83–86.

14. Разумов М.С. Повышение производительности формообразования многогранных наружных поверхностей посредством планетарного механизма: автореф. дис. ... канд. техн. наук. – Курск, 2011. – 18 с.

Использование в промышленности (машино-, автомобиле-, приборостроении) профильных валов вместо шлицевых и шпоночных является перспективным в плане обеспечения достаточной надежности тяжелонагруженных соединений [1, 2, 3]. В настоящее время существует несколько способ по реализации формообразования данного вида валов, однако в условиях автоматизации конструкторско-технологической подготовки производства многие вопросы, связанные с прочностными расчетами [6, 8, 10, 13, 14] очень актуальны.

Для решения данной проблемы было предложено производить оценку прочности соединения исходя из расчета на изгиб с кручением [5, 9, 11, 12]. Требуется с большой точностью определить значение осевых и полярного моментов инерции поперечного сечения [4, 7] (рис. 1).

Расчет моментопередающих соединений на кручение в основном заключается в определении максимального касательного напряжения в поперечном сечении. Основная расчетная формула для определения тангенциального напряжения в точке с координатой y ‒

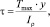
где Тmax – максимальный крутящий момент, передаваемый валом; Iρ – полярный момент инерции сечения.

Когда сечение имеет простую форму, определение Iρ не составляет никаких сложностей. В общем виде его можно представить в виде суммы двух осевых моментов инерции

Iρ = IХс + IYс. (1)

Моментопередающее соединение имеет в поперечном сечении достаточно сложный профиль.

Высота центрального треугольника равна

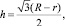(2)

где R ‒ радиус описанных окружностей из вершин центрального треугольника.

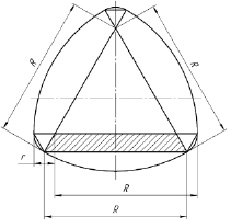
Рис. 1. Плоское сечение моментопередающего вала

Расстояние от оси Х1 до центральной Хс определяется по формуле

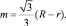
Полярный момент инерции большего кругового сегмента относительно Хс:

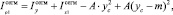(3)

где A – площадь кругового сегмента.

Теперь определим осевые моменты инерции IX1, Iy и площадь кругового сегмента (рис. 2 и 3).

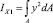и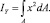

При вычислении IX1 элементарная площадка расположена на расстоянии y = R∙sin α. Соответственно, dy = Rcos αdα. Угол может изменяться в пределах 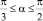. Площадь кругового сегмента равна

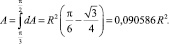(4)

Момент инерции относительно оси IX1 равен

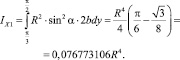(5)

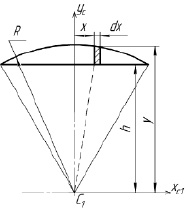
Рис. 2. Определение осевого момента инерции кругового сегмента относительно оси YC

Теперь вычислим Iy

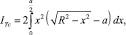
где x = Rcos t – расстояние от оси Y до элементарной площадки.

Удобнее всего этот интеграл брать в параметрическом виде. Введем параметр t следующим образом:

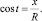
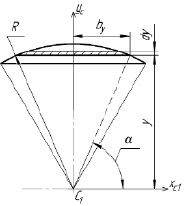
Рис. 3. Определение осевого момента инерции кругового сегмента относительно оси XC1

Соответственно

, .

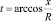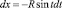Следовательно, у нас поменяются пределы интегрирования:

при x1 = 0,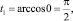

при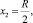

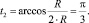
В итоге получим

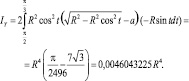(6)

Статический момент кругового сегмента относительно оси X1 равен

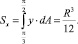(7)

Координата центра тяжести определяется по формуле

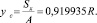(8)

Окончательно, подставляя (4), (5), (6) и (8) в (3), получаем полярный момент инерции большего кругового сегмента:

Полярный момент инерции меньшего кругового сегмента относительно Хс:

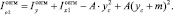
Все переменные находятся аналогично. Следовательно, полярный момент малого кругового сегмента

Вычислим полярные моменты малого и большого треугольника относительно Х.

Момент инерции относительно оси Х большого треугольника

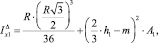
где 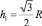– высота треугольника; 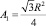– площадь треугольника.

Следовательно,

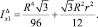
Момент инерции относительно оси Y большого треугольника

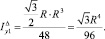
Полярный момент большего треугольника равен

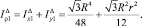
Аналогично находится полярный момент малого треугольника:

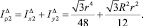
Полярный момент центрального треугольника равен

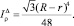
Окончательный полярный момент фигуры вычисляется по формуле

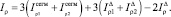
Введём новую переменную

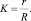
Тогда

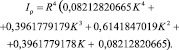
С помощью полученных зависимостей становится возможным определить с высокой степенью точности нормальные и касательные напряжения, возникающие в профильном соединении при передаче крутящего момента. Указанные зависимости могут быть использованы при автоматизированном прочностном расчете соединения по 3-ей теории прочности, что позволит сократить время на конструкторско-технологическую подготовку производства изделий, содержащих в своей конструкции соединения на базе треугольника Рёло.

Работа выполнена в рамках гранта Президента РФ по государственной поддержке молодых российских ученых ‒ кандидатов наук МК-2653.2014.8.

Рецензенты:

Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск;

Яцун С.Ф., д.т.н., профессор, заведующий кафедрой механики, мехатроники и робототехники, ЮЗГУ, г. Курск.

Работа поступила в редакцию 16.02.2015.

Библиографическая ссылка