В статье рассматривается математическая модель процесса аккумуляции тепловой энергии в стационарном переключающемся регенеративном теплоутилизаторе (СПРТ) [1]. Под СПРТ понимается автономное вентиляционное устройство, имеющее в своем составе регенеративный теплообменник, устанавливаемое в конструкцию стены или окна и обслуживающее одно или два смежных помещения. В статье рассматривается регенеративный теплоутилизатор типа УВРК-50, в котором в качестве теплообменника используется регенеративная насадка из полиэтилена. Принцип работы теплоутилизатора типа УВРК-50 характеризуется двумя режимами работы: режим аккумуляции и режим регенерации. В режиме аккумуляции устройство работает на вытяжку и происходит нагрев регенеративной насадки внутренним вытяжным воздухом. В режиме регенерации устройство работает на приток и происходит нагрев приточного воздуха насадкой. В данной статье рассматривается процесс аккумуляции тепловой энергии.
Для точного анализа термодинамических процессов, происходящих в регенеративной насадке устройства, требуется составление математической модели.
На данный момент недостаточно внимания уделяется теплообменникам типа СПРТ. Существующие математические модели разработаны либо для регенеративных теплоутилизаторов, работающих при высокой температуре теплоносителя [2], либо регенеративных теплоутилизаторов с роторной (вращающейся) насадкой [4]. Единственная математическая модель, разработанная для СПРТ, приведена в источнике [1]. Данная модель построена и численно исследована с помощью разностной схемы. Но такие вопросы, как существование и единственность решения, а также аналитические способы нахождения решения, пока не исследованы. Аналитический способ нахождения решения задачи актуален с точки зрения разработки алгоритмов расчета тепловых характеристик процесса и оптимального управления работой теплоутилизатора.
Целью настоящей статьи является разработка математической модели процесса аккумуляции тепловой энергии в виде смешанной задачи, состоящей из системы двух дифференциальных уравнений; доказательство существования единственного решения смешанной задачи; составление приближенного решения смешанной задачи.
Разработка математической модели
Введем следующие обозначения: ТВ(τ, z) – температура воздуха в момент времени τ в точке z, где τ ≥ 0, 0 ≤ z ≤ L, °С; ТН(τ, z) – температура насадки в момент времени τ в точке z, где τ ≥ 0, 0 ≤ z ≤ L, °С; Gак – расход воздуха на этапе аккумуляции, м3/ч; сВ – теплоемкость воздуха, кДж/кг·°С; ρВ – плотность воздуха, кг/м3; SВ – площадь сечения канала, по которому проходит воздух, м2; П – периметр сечения канала, по которому проходит воздух, м; α – коэффициент теплоотдачи воздуха, Вт/м2·°С; Тin – температура помещения, откуда поступает тепловая энергия,·°С; Тout – температура внешней среды, куда поступает часть тепловой энергии,·°С; λН – теплопроводность материала насадки, Вт/ м·°С.
Построим математическую модель процесса нагрева воздуха в проходном канале. Для этого отметим, что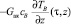 
– количество тепла, поступающего в проходное сечение в точке z в момент времени τ; 
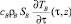– количество тепла, затрачиваемое на нагревание проходного сечения в точке z в момент времени τ; 
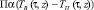– количество тепла, передаваемого от воздуха насадке в проходном сечении в точке z в момент времени τ.
Уравнение баланса тепловой энергии в проходном сечении в точке z в момент времени τ:
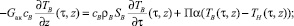τ > 0, 0 < z < L. (1)
Уравнение (1) представляет собой математическую модель процесса нагрева воздуха в проходном канале. При этом необходимо учитывать начальное условие
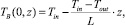0 ≤ z ≤ L, (2)
т.е. в начальный момент времени температура в проходном канале распределена линейно между Тin и Тout, а также граничное (краевое) условие
ТB(τ, 0) = Тin, τ ≥ 0, (3)
т.е. на левом конце проходного канала температура все время постоянна и равна комнатной Тin.
Таким образом, получаем начально-краевую (смешанную) задачу (1), (2), (3) для неизвестной функции ТВ(τ, z).
Теперь построим математическую модель процесса нагрева насадки. В процессе нагрева насадки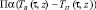 
– количество тепловой энергии, поступающее от воздуха насадке в проходном сечении в точке z в момент времени τ; 
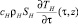– количество тепловой энергии, расходуемое на нагревание насадки в точке z в момент времени τ; 
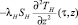– количество тепловой энергии, перемещаемое внутри насадки по закону Фурье.
Уравнение баланса тепловой энергии в поперечном сечении насадки в точке z в момент времени τ:
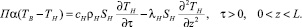(4)
Уравнение (4) представляет собой математическую модель процесса нагрева насадки. Необходимо учитывать начальное условие
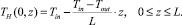, (5)
т.е. в начальный момент времени температура в насадке распределена линейно между Тin и Тout и граничные (краевые) условия
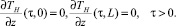(6)
т.е. концы насадки изолированы все время. Таким образом, получаем начально-краевую (смешанную) задачу (4), (5), (6) для неизвестной функции ТH(τ, z).
Смешанная задача (1)–(6) есть математическая модель процесса аккумуляции тепловой энергии в термодинамической системе «воздух – насадка».
Единственность решения
Решением начально-краевой задачи (1)–(6) назовем пару функций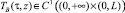 
, 
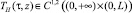, являющуюся решением системы уравнений (1), (4), и удовлетворяющую начальным условиям (2), (5) и краевым условиям (3), (6). Общеизвестным методом энергетических равенств и неравенств ([3]) докажем, что решение (ТВ(τ, z), ТH(τ, z)) смешанной задачи (1)–(6) единственно. Для этого достаточно показать, что если начальные значения ТВ(0, z), ТH(0, z) и граничное значение ТВ(0, z) тождественно равны нулю, то функции ТВ(τ, z) и ТH(τ, z) также тождественно равны нулю.
В силу уравнений (1) и (4) имеем
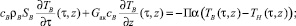
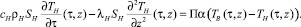
Первое равенство умножим на ТВ(τ, z), второе – на ТH(τ, z), затем сложим их и проинтегрируем по z в пределах от 0 до L:
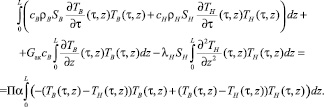
Заметим, что
1) 
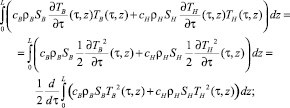
2) 
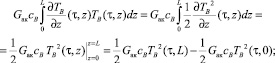
3) 
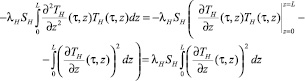в силу граничных условий (6);
4) 
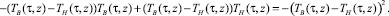
Следовательно, имеем
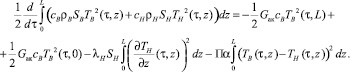
Отсюда следует, что если ТВ(τ, 0) ≡ 0, то
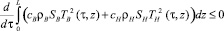при τ > 0,
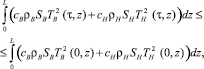при τ > 0.
Если к тому же ТВ(0, z) ≡ 0 и ТH(0, z) ≡ 0, то
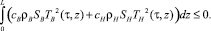
Значит, ТВ(τ, z) ≡ 0 и ТH(τ, z) ≡ 0. Единственность решения доказана.
Приближенное решение
Смешанную задачу (1)–(6) перепишем в следующем виде:
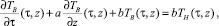τ > 0, 0 < τ < L, (7)
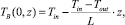0 ≤ τ ≤ L, ТB(τ, 0) = Тin, τ ≥ 0, (8)
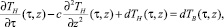τ > 0, 0 < τ < L, (9)
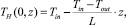0 ≤ τ ≤ L, 
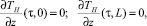τ > 0, (10)
где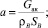 
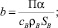
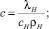
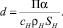
В силу (7) и (8) функцию ТВ(τ, z) можно выразить функцией ТH(τ, z):
ТВ(τ, z) = ΦВТH(τ, z), (11)
где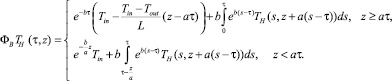 
В силу (9) и (10) функцию ТH(τ, z) можно выразить функцией ТВ(τ, z):
ТH(τ, z) = ΦHТВ(τ, z), (12)
где
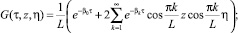
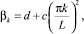k = 0, 1, 2, ...
Интегральные представления (11) и (12) выводятся из общеизвестных формул решения смешанных задач вида (7), (8) и (9), (10) (см., напр., [5]).
Таким образом, смешанная задача (7)–(10) равносильна системе интегральных уравнений (11), (12). Систему (11), (12) решим методом последовательных приближений ([5]). А именно построим следующие последовательности функций:
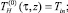
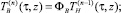
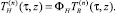(13)
Последовательность функций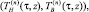 
n = 1, 2, ... сходится к решению (ТH(τ, z), ТВ(τ, z)) смешанной задачи (7)–(10):
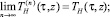
Поэтому при больших номерах n пару функций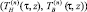 
можно взять в качестве приближенного решения (ТH(τ, z), ТВ(τ, z)) смешанной задачи (7)–(10):
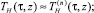
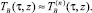
При больших номерах n и фиксированных моментах времени τ графики функций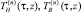 
представлены на рис. 1 и 2.
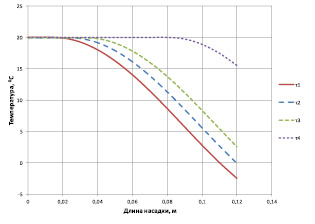
Рис. 1. График зависимости изменения температуры воздуха от длины насадки при четырех фиксированных моментах времени τ
В итоге работы можно сделать вывод, что графические результаты по предложенной математической модели в определенной мере отвечают реальным процессам теплообмена в СПРТ.
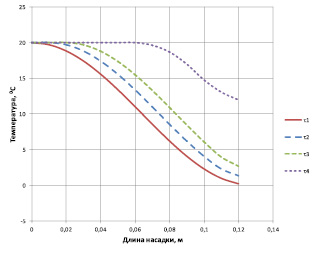
Рис. 2. График зависимости изменения температуры насадки от длины насадки при четырех фиксированных моментах времени τ
Необходимо отметить, что в рассмотренной модели коэффициент теплоотдачи воздуха α считается известной величиной. Но в реальности величина α существенно зависит от потока воздуха Gак и самого процесса нагрева, поэтому было бы естественным величину α также считать неизвестной. В этом случае математическую модель нужно скорректировать так, чтобы величину α можно было однозначно находить наряду с неизвестными функциями ТВ и ТН. Для этого необходимо ввести дополнительное условие, позволяющее находить α.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ в рамках выполнения государственного задания высшим учебным заведениям.
Рецензенты:
Горбунов В.А., д.ф.-м.н., профессор, главный специалист Общества с ограниченной ответственностью Научно-производственный центр «ЭнергоКИТ», г. Вологда;
Игонин В.И., д.т.н., профессор, главный конструктор Общества с ограниченной ответственностью Научно-производственный центр «Информационные и энергетические технологии» (малое инновационное предприятие ООО НПЦ «Инэнтех»), г. Вологда.
Работа поступила в редакцию 17.10.2014.