Современный рынок электрической энергии характеризуется устойчивыми тенденциями к её удорожанию и переходом на дифференцированную тарификацию, при которой стоимость электрической энергии изменяется через определенный фиксированный промежуток времени (каждый час или, в ближайшем будущем, даже каждые 15 минут), который в дальнейшем будем называть периодом фиксированной величины тарифа. Эти тенденции обуславливают потребность в устройствах, способных управлять процессами покупки, распределения и использования электрической энергии её конечными потребителями таким образом, чтобы суммарные затраты последних были минимальными. Особенно актуально это стоит в микросетях, функционирование которых реализуется по технологии Smart Grid. В них с учётом юридических аспектов гораздо легче, чем в коммерческих сетях, технически реализовать процессы торговли электрической энергией по свободно формируемым ценам.
Важнейшим этапом создания подобного рода устройств является разработка механизма принятия решений. Во-первых, он позволит потребителям электрической энергии формировать график потребления, то есть определять, как должен изменяться уровень потребления энергетических услуг в течение периода планирования. Во-вторых, этот механизм должен осуществлять планирование работы электрических приборов на основе заранее сформированного графика потребления с учетом текущих тарифов на электрическую энергию так, чтобы финансовые затраты со стороны потребителя были минимальными.
Ключевой задачей при разработке такого механизма является задача оптимизации, решение которой позволит подобрать такой график работы электрических приборов, при котором затраты потребителя будут минимальными.
При решении данной задачи также важно учитывать качество потребляемой электрической энергии. Основным показателем, характеризующим качество электрической энергии, является коэффициент несинусоидальности напряжения THD [1].
Отклонение THD от нормированных значений проявляется в виде экономического ущерба у потребителей электрической энергии. Данный ущерб имеет электромагнитную и технологическую составляющие. Электромагнитная составляющая определяется в основном дополнительными потерями активной мощности и энергии и сокращением ресурса электрооборудования, например ввиду ускоренного старения изоляции. Технологическая составляющая ущерба связана с увеличением длительности производственного процесса, со снижением производительности электрооборудования и, следовательно, с увеличением удельного электропотребления на единицу произведенной продукции.
Целевая функция, отражающая финансовые затраты потребителя, имеет вид
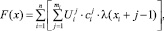(1)
где n – количество электрических приборов; mi – время работы i-го прибора (количество часов);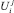 
– количество энергии, потребляемой i-м прибором за j-й час работы, т.е. каждому электрическому прибору соответствует вектор 
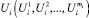; xi – время (час) начала работы i-го прибора, причем 0 < xi < 23, 
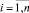; λ(t) – тариф на электрическую энергию, 0 < t < 23 (в нашем случае t = xi + j – 1 соответствует j-му часу работы электрического прибора при условии, что данный прибор начал работать в момент времени xi); 
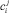– коэффициент, учитывающий влияние качества потребляемой электрической энергии на потребляемую мощность i-м электрическим прибором за j-й час работы, т.е. каждому электрическому прибору соответствует вектор 
.
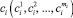Дискретность во времени коэффициента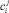 
хорошо согласуется с требованиями Открытого протокола Smart Grid (OSGP), по которому требуется записывать в память микроконтроллера все отклонения THD от нормы [1]. В общем случае 
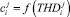. Существование данной функции является очевидным, но ее конкретный вид зависит от многих факторов, трудно поддающихся формализации. Поэтому на данном этапе для определения 
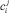следует применять экспертные методы анализа или использовать полные математические модели микро Smart Grid для получения качественного статистического материала [2].
Таким образом, для минимизации затрат потребителя необходимо решить следующую задачу оптимизации:
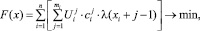(2)
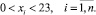(3)
Решением задачи является оптимальный график работы электрических приборов (в рассматриваемом случае – почасовой), представленный вектором x(x1, x2, ..., xn).
Наиболее подходящим методом решения рассмотренной задачи оптимизации является метод роя частиц (Particle Swarm Optimization) [3, 4].
Метод роя частиц относится к методам искусственного интеллекта и применим для поиска приближенных решений крайне сложных или нерешаемых задач нахождения числовых максимумов и минимумов. Под частицами понимаются абстрактные объекты, обладающие двумя свойствами: позицией и скоростью. При этом позиция частицы представляет собой возможное решение задачи оптимизации, а скорость частицы отражает ее направление к новому, предположительно лучшему, решению. Количество частиц в рое задается произвольным образом. Каждой частице также известны наилучшая позиция, найденная ею на данный момент, и наилучшая позиция среди всех частиц. При этом под наилучшей позицией понимается позиция, соответствующая минимальному (максимальному) значению целевой функции.
Канонический вариант метода описывает движение частиц следующим образом [5]:
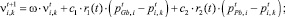(4)
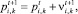(5)
где P(p1,k, ..., pn,k) и V(v1,k, ..., vn,k) – позиция и скорость k-й частицы; коэффициенты ω; c1, c2 – весовая доля инерции, когнитивная и глобальная весовые доли соответственно; r1(t), r2(t) – случайные числа, лежащие в диапазоне [0, 1];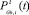 
– лучшая известная позиция, найденная на данный момент среди всех частиц в рое; 
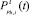– лучшая позиция i-й частицы, найденная ею на данный момент.
В качестве примера было рассмотрено численное решение задачи (2)–(3) для двух переменных со следующими параметрами: количество частиц в рое – 50; время работы первого прибора – 2 часа время работы второго прибора – 3 часа; c1 = c2 = 1,4962; ω = 0,7298.
Тариф на электрическую энергию приведен в табл. 1.
Таблица 1
Тариф на электрическую энергию
|
Время суток (ч) |
0:00–1:00 |
1:00–8:00 |
8:00–9:00 |
9:00–14:00 |
14:00–21:00 |
21:00–23:00 |
|
Стоимость электрической энергии ($/кВт•ч) |
0,0814 |
0,1408 |
0,0814 |
0,1408 |
0,3564 |
0,1408 |
Допустим, с учетом коэффициентов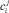 
, первый прибор потребляет 1 и 2 кВт•ч за первый и второй часы работы соответственно; второй прибор – 2 кВт·ч за первый час и по 1 кВт·ч во второй в третий часы работы. Таким образом, для того, чтобы минимизировать затраты, необходимо первый прибор включить в 07:00, а второй прибор – в 00:00 или в 08:00.
Вычисления производились с помощью пакета MATLAB R2011b. Результаты десяти численных экспериментов и график целевой функции приведены ниже.
Таблица 2
Результаты численного эксперимента
|
Номер эксперимента |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Результат [x1, x2] |
[7, 8] |
[7, 8] |
[7, 8] |
[7, 8] |
[7, 0] |
[7, 8] |
[7, 8] |
[7, 0] |
[7, 0] |
[7, 0] |
|
Число итераций |
105 |
827 |
1221 |
2122 |
121 |
104 |
774 |
125 |
270 |
288 |
Таким образом, применение метода роя частиц позволяет успешно решать задачи оптимизации, связанные с нахождением наилучших режимов работы электрических приборов с целью минимизации затрат потребителя.
С целью адаптации метода для решения целочисленных задач и повышения его быстродействия были внесены следующие изменения:
– значение скорости на каждом временном шаге округлялось до наименьшего целого;
– если позиция частицы осталась той же, что и на предыдущем шаге (т.е. скорость i-й частицы оказывалась равной нулю), то значение скорости определялось следующем образом:
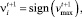(6)
где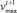 
– максимальная по абсолютному значению скорость среди всех частиц на данном временном шаге.
Для проведения сравнительного анализа канонического и модифицированного методов решения задачи был проведен численный эксперимент, в ходе которого рассматривалось численное решение задачи (2)–(3) для двух переменных. Решением данной задачи является вектор x, принимающий значения [7, 8] или [7, 0]. В результате решения задачи каноническим и модифицированным методами были получены следующие результаты:
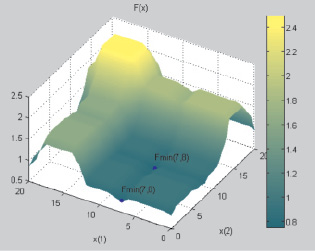
График целевой функции
Таблица 3
|
Номер итерации |
Канонический метод «роя частиц» |
Модифицированный метод «роя частиц» |
||
|
Результат [x1 x2] |
Кол-во итераций |
Результат [x1 x2] |
Кол-во итераций |
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
[7 0] |
701 |
[7 8] |
20 |
|
2 |
[7 8] |
252 |
[6 0] |
5 |
|
3 |
[7 8] |
149 |
[7 8] |
12 |
|
4 |
[7 8] |
677 |
[7 0] |
13 |
|
5 |
[7 8] |
537 |
[7 8] |
21 |
|
6 |
[7 8] |
86 |
[7 8] |
27 |
|
7 |
[7 8] |
96 |
[6 0] |
6 |
|
8 |
[7 8] |
526 |
[7 8] |
24 |
|
9 |
[7 8] |
174 |
[7 8] |
103 |
|
10 |
[0 0] |
200 |
[7 8] |
21 |
|
11 |
[7 8] |
170 |
[6 0] |
17 |
|
12 |
[7 8] |
788 |
[7 8] |
30 |
|
13 |
[7 8] |
732 |
[7 0] |
23 |
|
14 |
[7 8] |
2117 |
[7 0] |
18 |
|
15 |
[7 8] |
345 |
[7 0] |
8 |
|
16 |
[7 8] |
131 |
[7 8] |
37 |
|
17 |
[7 0] |
1542 |
[0 0] |
3 |
|
18 |
[7 0] |
107 |
[6 5] |
6 |
|
19 |
[7 8] |
336 |
[7 0] |
4 |
|
20 |
[7 8] |
152 |
[7 8] |
25 |
|
Среднее количество итераций |
||||
|
491 |
21 |
|||
Таким образом, тестирование модифицированного метода «роя частиц» для решения целочисленной задачи оптимизации графика потребления электрической энергии позволяет сделать вывод о существенном преимуществе данного метода в скорости по сравнению с каноническим.
Однако точность вычислений уступает каноническому методу в связи с высокой вероятностью сходимости частиц к локальному экстремуму, что позволяет сделать вывод о необходимости дальнейшего усовершенствования метода для исключения возможности сходимости частиц к локальному экстремуму, в частности применения метода «растяжения» (stretching technique) [6].
Рецензенты:
Сергеев В.А., д.т.н., профессор, директор Ульяновского филиала Института радиотехники и электроники им. В.А. Котельникова РАН, г. Ульяновск;
Белей В.Ф., д.т.н., профессор, заведующий кафедрой электрооборудования судов и электроэнергетики, ФГБОУ ВПО «Калининградский государственный технический университет», г. Калининград.
Работа поступила в редакцию 15.09.2014.