QUANTUM-CHEMICAL STUDY OF STRUCTURE AND PROPERTIES OF THE LEAD HALCOGENIDES

Poleschuk O.KH. 1, 2 Egorov N.B. 2 Polysinskii E.V. 2 Ermakhanov M.N. 3 Seidakhmetov P.A. 3 Ivanovskiy A.L. 4

1 Tomsk State Pedagogical University

2 Tomsk Polytechnic University

3 M.O. Auezov South Kazakhstan University

4 Institute of Solid State Chemistry of Ural Branch of Russian Academy of Sciences

Article in PDF

1429 KB

In the present work, at the level of density functional theory B3LYP/SDD and BP86/TZ2P+ quantum-chemical calculations of lead, sulfur, selenium and tellurium compounds, and lead chalcogenides have been carried out. It has been shown that this level of theory is applicable for estimation of geometrical parameters, Raman and IR spectra, and thermodynamic characteristics of the chalcogenides lead compounds. The resulting correlation ratio between the experimental and calculated by B3LYP/SDD and BP86/TZ2P+ density functional methods dissociation energies indicate that the calculated thermodynamic parameters of sulfur, selenium and tellurium compounds are close enough to each other and to the experimental values, and the error calculation by ADF method is not more than 8%. It is shown that the semi-empirical PM3 method and B3LYP/SDD in lead halides correctly describe the geometrical parameters, enthalpy and entropy of formation. In this case it was shown that the relationship between the calculated and experimental enthalpy of formation and dissociation energies fall on separate lines for the coordination of lead compounds 2 and 4 on the basis of both calculated methods. It has been shown that using of FLAW in solid state and B3LYP/SDD in gas phase lead to fairly reliable values of the bond length and the lattice constant of lead chalcogenides. Separation of the chemical bond energy of lead-chalcogen on covalent and ionic components showed that a larger contribution is covalent component.

Density functional theory

B3LYP/SDD

BP86/TZ2P

FLAW

Raman spectra

the lattice constant

covalence bond

1. Plehanov V.G. Izotopicheskaja inzhenerija // Uspehi fizicheskih nauk. -2000. – T. 170. – PP. 1245–1252.

2. Plehanov V.G. Izotopicheskie jeffekty v dinamike reshetki // Uspehi fizicheskih nauk. – 2003. – T. 173. – PP. 711–738.

3. Zhernov A.P., Injushkin A.V. Vlijanie kompozicii izotopov na fononnye mody. Staticheskie atomnye smeshhenija v kristalla // Uspehi fizicheskih nauk. – 2001. – T. 171. – PP. 827–854.

4. Poleshhuk O.H., Egorov N.B., Zherin I.I., Ivanovskij A.L. Ispol'zovanie funkcionala plotnosti dlja ocenki izotopnyh sdvigov v soedinenijah svinca // Butlerovskie soobshhenija. – 2011. – T. 24. – PP. 69–75.

5. Bacanov S.S. Strukturnaja himija. Fakty i zavisimosti. M. – Dialog MGU – 2000. – 292 p.

6. Haller E.E. Isotopically controlled semiconductors // Solid State Communications. – 2005. – V. 133. – РP. 693-707.

7. Gaussian 03, Revision B03. Frisch M.J., Trucks G.W., Schlegel H.B., Gill P.M.W., Johnson B.G., Robb M.A., Cheeseman J.R., Keith T., Petersson G.A., Montgomery J.A., Raghavachari K., Al-Laham M.A., Zakrzewski V., Ortiz J.V., Foresman J.B., Closlowski J., Stefanov B.B., Nanayakkara A., Challacombe M., Peng C.Y., Ayala P.Y., Chen W., Wong M.W., Andress J.L., Replogle E.S., Gomperts R., Martin R.L., Fox D.J., Binkley J.S., Defress D.J., Baker J., Stewart, J.P. Head-Gordon, Gonzales C., Pople J.A. Gaussian, Inc: Pittsburg, PA. 2003.

8. Becke A.D. Density-functional thermochemistry. III. The role of exact exchange // J. Chem. Phys. -1993. – V. 98. – РP. 5648–5653.

9. Lee C., Wang Y., Parr R.G. Development of the Colle-Salvetti correlation energy formula into a functional of the electron density // Phys. Rev. – 1988. – V. 37. – РP.785–789.

10. Curtiss L.A., Raghavachari K., Redfern P.C., Pople J.A. Assessment of Gaussian-2 and density functional theories for the computation of enthalpies of formation // J. Chem. Phys. – 1997. – V. 106. – РP. 1063–1080.

11. ADF2004.01. SCM. Theoretical Chemistry. Amsterdam:Vrije Universiteit. http://www.scm.com

12. Velde G. te, Bickelhaupt F.M., Gisbergen S.J.A., Guerra C. Fonseca, Baerends E. J., Snijders J. G., Ziegler T. Chemistry with ADF // J. Comput. Chem. – 2001. – V. 22. – PР. 931–940.

13. Blaha P., Schwarz K., Madsen G.K.H. et al., WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties. Vienna Univ. Technol.: Vienna. 2001.

14. Perdew J.P., Burke K., Ernzerhof M. Generalized Gradient Approximation Made Simple // Phys. Rev. Lett. – 1996. – V. 77. – PР. 3865–33868.

15. Blochl P.E., Jepsen O., Anderson O.K. Improved tetrahedron method for Brillouin-zone integrations // Phys. Rev. – 1994. – V. B49. – РP. 16223–16230.

16. Nakamoto K. Infrared and raman spectra of inorganic and coordination compounds. Part 1. N.Y. – Wiley – 1997. – 387 p.

17. NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Eds. P.J. Linstrom and W.G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, http://webbook.nist.gov, (retrieved May 20, 2010).

18. Frenking G., Wichamann K., et al, Towards a rigorously defoned quantum chemical analysis of the chemical bond in donor-acceptor complexes // Coord. Chem. Rev. – 2003. – V. 238-239. – РP. 55–82.

Достаточно хорошо известно, что халькогениды металлов представляют значительный интерес в различных технологических областях, таких как микроэлектроника, электрооптика, нелинейная оптика, фотокатализ, фотоэлектрохимия. В частности, сульфид свинца вследствие почти идеальной монокристаллической формы – один из самых используемых и исследуемых полупроводников. Благодаря наличию прямых электронных переходов, PbS нашел применение как инфракрасный детектор, используется в лазерных технологиях [6, 1], а также как материал для исследования свойств и поиска прикладного применения квантовых точек [2].

Наряду с экспериментальными исследованиями развивается теория фононных спектров с использованием моделей – жестких ионов, деформируемых диполей, зарядов на связях, а также в рамках теории функционала плотности [3, 4].

Цель работы – анализ применимости теории функционала плотности к оценке геометрических, спектральных и термодинамических характеристик халькогенидов свинца.

Материалы и методы исследования

При проведении квантово-химических расчетов нами использован стандартный пакет программ GAUSSIAN’03W [7]. Расчеты проводили гибридным методом функционала плотности B3LYP, с обменным функционалом Беке В3 и корреляционным функционалом Ли, Янга и Пара (LYP) [8, 9]. Этот метод является общепринятым в настоящее время для описания термодинамических характеристик и колебательных спектров [10]. В качестве базисного состояния использован псевдопотенциал SDD для атома свинца и D95 double-dzeta базис для остальных атомов. Геометрии всех рассчитанных молекул были полностью оптимизированы, отсутствие мнимых частот колебаний подтверждало их стационарный характер. Энергии диссоциации рассчитанных соединений были скорректированы с учетом нулевой колебательной энергии (ZPVE) и приведены к стандартным условиям (298, 15К, 1 атм) с использованием термической поправки к энтальпии и свободной энергии. Нами также были проведены расчеты по программе ADF'2004 (Амстердамский функционал плотности) [10]. Мы использовали обменный функционал OPTX, объединенный с корреляционным функционалом PBE, используя полноэлектронный трипл-ζ с учетом поляризации базисного набора Слейтеровских орбиталей (BP86/TZ2P+) [12]. Все вышеприведенные расчеты проведены для соединений свинца, серы, селена и теллура, а также PbS, PbSе и PbTe, находящихся в газовой фазе. Расчет электронной структуры и характеристик PbS, PbSе и PbTe, находящихся в кристаллическом состоянии проведен полно-потенциальным линейным методом присоединенных плоских волн (FLAPW, код WIEN2k [13]) с обобщенной градиентной аппроксимацией (GGA) обменно-корреляционного потенциала [14] с полной структурной оптимизацией. Плотности электронных состояний получены методом тетраэдров [15].

В этом случае для расчетов использовались кубические (типа В1, простр. группа № 225, Fm-3m), моносульфид, моноселенид и монотеллурид свинца PbS, PbSe, PbTe; атомные координаты: Pb (0;0;0) и S, Se,Te (1/2;1/2;1/2).

Результаты исследования и их обсуждение

Для оценки «качества» квантово-химических расчетов халькогенидов свинца необходимо опираться на некоторые физико-химические свойства подобных соединений, для которых известны экспериментальные достаточно надежные значения. В качестве последних нами использованы длины связей, частоты валентных и деформационных колебаний в ИК-спектрах соединений свинца, серы, селена и теллура, а также экспериментальные значения ширины запрещенной зоны кристаллических халькогенидов и энергии диссоциации соединений серы, селена и теллура в газовой фазе (табл. 1). Из результатов расчета следует, что оптимизированные методом B3LYP/SDD длины связей в соединениях серы, селена и теллура пропорциональны экспериментальным значениям [5], и наблюдаются хорошие корреляционные соотношения между ними:

Таблица 1

Экспериментальные и рассчитанные энергии диссоциации соединений серы, селена и теллура

Молекула	Экспериментальная энергия диссоциации связи, кДж/моль	Рассчитанная методом ADF энергия диссоциации связи, кДж/моль	Рассчитанная методом B3LYP/6-31G(d) энергия диссоциации связи, кДж/моль
1	2	3	4
SF	343	572	527
SCl	277	401	432
SH	345	495	543
SO	522	781	799
SP	444	718	743
SC	714	994	996
TeB	354	485	477
SeAl	338	468	438
TeAl	268	343	372
SeIn	247	359	414
TeIn	218	326	364
SeP	364	505	574
SeAs	352	490	564
TeAs	312	445	519
SeS	371	547	490
TeS	339	502	469
SeTe	292	468	446
SeO	465	694	623
SeC	590	869	802
Se₂	333	510	468
SeH	311	493	439
SeSi	534	731	694
SeGe	485	694	673
SeSn	401	635	631
Te2	260	390	422
TeSi	448	631	623
TeO	376	550	602
TeCu	229	320	351
TeGe	430	610	614

Для соединений серы R(эксп.) = 0.06+0.994R (расч.) r = 0.999; s = 0.01; n = 6 (1)

Для соединений селена R(эксп.) = 0.957R (расч.) r = 0.995; s = 0.04; n = 18 (2)

Для соединений теллура R(эксп.) = 0.969R (расч.) r = 0.993; s = 0.04; n = 10 (3)

Здесь и далее r – коэффициент корреляции, s – стандартное отклонение, и n – число соединений.

Для галогенидов свинца из результатов расчета следует, что оптимизированные методом B3LYP/SDD валентные углы Hal-Pb-Hal близки к экспериментальным значениям [5] (около 98-100 ^о), а длины связей Pb-Hal (Hal = F, Cl, Br, I, Me) Pb(II) и Pb(IV) соединений дают хорошее корреляционное соотношение (рис. 1).

Рассчитанные обоими методами частоты ИК- и Рамановских спектров галогенидов свинца достаточно близки к экспериментальным значениям (рис. 2, 3) с коэффициентом корреляции 0.998 и стандартным отклонением 9.

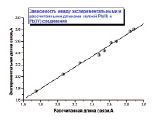
pol1.tif

Рис. 1. Зависимость между экспериментальными и рассчитанными методом B3LYP/SDD длинами связей соединений Pb(II) и Pb(IV)

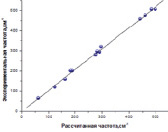
pol2.tif

Рис. 2. Зависимость между экспериментальными и рассчитанными методом B3LYP/SDD ИК частотами галогенидов свинца

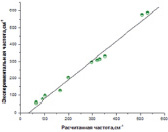
pol3.tif

Рис. 3. Зависимость между экспериментальными и рассчитанными методом ADF ИК частотами галогенидов свинца

Кроме того, рассчитанные частоты ИК- и Рамановских спектров соединений селена и теллура хорошо ложатся на прямолинейные зависимости [16]:

Для соединений серы ω(эксп.) = 46+0.960 ω(расч.) r = 0.998; s = 35; n = 34 (4)

Для соединений селена ω(эксп.) = 59+0.996 ω(расч.) r = 0.993; s = 57; n = 91 (5)

Для соединений теллура ω(эксп.) = 21+1.07 ω(расч.) r = 0.993; s = 27; n = 67 (6)

Необходимо отметить, что близкий к единице в соотношениях (1-6) коэффициент перед рассчитанными параметрами указывает на высокую надежность результатов использования функционала плотности и базисного SDD состояния.

Нами получены также достаточно надежные линейные корреляционные зависимости (7 и 8), которые свидетельствует о том, что проведенные расчеты соединений селена и теллура методами B3LYP/SDD и ВР86/TZ2P+ правильно описывают не только геометрию, но и термодинамические параметры, в частности, энергии диссоциации (D₀). Энергия диссоциации соединений серы, селена и теллура определялась как разница между энергией соединения и энергиями составляющих их атомов с поправкой на нулевую энергию. Рассчитанные энергии диссоциации, отнесенные к числу связей, сравнивались с экспериментальными средними энергиями связей элемент-сера, селен и теллур [17] (Табл. 1). В результате получены корреляционные соотношения на основании обоих методов расчета в программах GAUSSIAN и ADF (рис. 3, 4):

GAUSSIAN: D₀ (эксп.) = -25 +0.73 D₀ (расч.) r = 0.963; s = 31; n = 29 (7)

ADF: D₀ (эксп.) = 1.8 +0.68 D₀ (расч.) r = 0.980; s = 23; n = 29 (8)

Полученные корреляционные соотношения указывают на то, что рассчитанные разными методами термодинамические параметры соединений серы, селена и теллура достаточно близки к другу и к экспериментальным значениям, а погрешность расчета методом ADF составляет не более 8 %.

Нами получены также достаточно надежные линейные корреляции (9-16), которые свидетельствуют о том, что проведенные расчеты галогенидов свинца методами РМ3 и B3LYP/SDD правильно описывают не только геометрию, но и термодинамические параметры, такие как энтальпии (ΔН^о) и энтропии (S^о) образования, энергии диссоциации (D_о) (табл. 2).

Таблица 2

Рассчитанные и экспериментальные [15] энтальпии образования, энтропии, энергии диссоциации галогенидов свинца, кДж/моль и Дж/моль.К

Соединение	ΔH^о, PM3	ΔH^о, эксп.	S^о, расч.	S^о, эксп.	-D_о, расч.	-D_о, эксп.
PbF₂	-375	-435.1	293	292.7	484	388
PbCl₂	-166	-174.0	318	317.2	388	304
PbBr₂	-119	-104.4	346	339.4	353	262
PbI₂	-18	-3.2	362	359.6	315	209
PbF₄	-617	-1133.4	345	333.5	341	327
PbCl₄	-259	-552.4	399	381.6	260	252
PbBr₄	-109	-456.4	445	426.2	229	199
PbI₄	56	-224.5	477	466.3	200	164

Необходимо отметить, что если энтропии образования ложатся на одну зависимость для соединений Pb(II) и Pb(IV), то зависимости между рассчитанными и экспериментальными энтальпиями образования и энергиями диссоциации наблюдаются отдельно для соединений свинца различной координации на основании обоих методов расчета в программах GAUSSIAN и ADF:

GAUSSIAN: S^o (эксп.) = -23 + 0.914S⁰ (расч.) r = 0.996; s = 5; n = 8 (9)

ADF: S^o (эксп.) = 10.6 + 0.97S⁰ (расч.) r = 0.998; s = 4; n = 7 (10)

Для Pb(II):

PM3: ΔH⁰ (эксп.) = 29 +1.23 ΔH⁰ (расч.) r = 0.999; s = 12; n = 4 (11)

GAUSSIAN: D_o (эксп.) = -108 +1.04 D₀ (расч.) r = 0.993; s = 11; n = 4 (12)

ADF: D_o (эксп.) = -44 +1.54 D₀ (расч.) r = 0.990; s = 13; n = 4 (13)

Для Pb(IV):

PM3: ΔH⁰ (эксп.) = -289 +1,35 ΔH⁰ (расч.) r = 0.997; s = 35; n = 4 (14)

GAUSSIAN: D_o (эксп.) = -62 +1.14 D₀ (расч.) r = 0.992; s = 11; n = 4 (15)

ADF: D_o (эксп.) = -28 +0.83 D₀ (расч.) r = 0.986; s = 14; n = 4 (16)

Рассчитанные обоими методами значения энергетического расстояния между занятыми и свободными молекулярными орбиталями (ΔЕ_{ВЗМО-НСМО}) хорошо согласуются с шириной запрещенной зоны в кристаллических хлоридах, бромидах и иодидах свинца [5] с коэффициентом корреляции 0.999 и стандартным отклонением 0.02.

Для дальнейшего изучения физико-химических свойств нами была проведена оптимизация элементарной ячейки PbS, PbSe и PbTe методом РМ3. Рассчитанные длины связей Pb-S, Pb-Sе и Pb-Te составила 3.5, 3.57 и 3.45 Å, что близко к экспериментальным значениям 2.97, 3.06 и 3.23 Å, а постоянные решеток оказались равными 6.5, 7.1 и 6.75 Å, что также близко к экспериментальному значению 5.94 Å для решетки сульфида свинца [16]. Необходимо отметить, что проведенный нами расчет по программе FLAPW кристаллических халькогенидов PbS, PbSе и PbTe дал лучшие значения постоянных решеток в 6.01, 6.23 и 6.57 Å, что практически совпадает с экспериментальными значениями.

Одной из наиболее важных характеристик полупроводников служит величина запрещенной щели. Расчет в твердом теле PbS, PbSе и PbTe дал значения 0.5, 0.44 и 0.70 эВ в газовой фазе – 0.38, 0.38 и 0.28 эВ по расчетам GAUSSIAN и 0.85, 0.36 и 0.25 эВ в ADF. Экспериментальная ширина зоны монокристалллического PbS равна 0.41 эВ [5]. Таким образом, можно предполагать, что проведенные расчеты газовой фазы и кристалла халькогенидов свинца дали достаточно близкие к эксперименту значения энергетических характеристик.

На основании расчета в твердом теле (FLAPW) и в газовой фазе методом ADF можно оценить химическую связь с точки зрения ионной (электростатической) и ковалентной (орбитальной) составляющей. Данные FLAPW указывают на смешанный ионно-ковалентный тип (рис. 4).

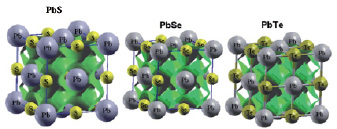
pol4.tif

Рис. 4. Изоэлектронные поверхности (ρ = 0.15 e/Å3) кубических (типа В1) PbS, PbSe и PbTe

При этом ионная составляющая создается за счет зарядовой поляризации в направлении Pb→ S, Pb→ Sе и Pb→ Те. В идеальной ионной модели зарядовые состояния Pb2+Hal2-, в реальности эффективные заряды атомов-компонентов будут меньше за счет ковалентного вклада. Ковалентная составляющая образуется за счет частичного перекрывания Halnp – Pb6s,6р состояний. Ковалентную составляющую можно иллюстрировать рис. 4, где видно перекрывание изоэлектронных поверхностей в направлении Pb-(S, Se,Te). В программе ADF энергия молекулы разделяется на несколько вкладов. Энергетические члены могут быть идентифицированы тремя главными компонентами химической связи, то есть отталкиванием Паули, электростатическим притяжением и ковалентным взаимодействием. Френкинг и соавторы [18] предложили, чтобы ∆Е_{элстат.} использовался для оценки силы электростатического связывания, а ∆Е_орб. – для ковалентного связывания. Наши результаты расчета халькогенидов свинца в газовой фазе также указывают на то, что химическая связь состоит из ионной и ковалентной составляющих с преобладанием последней (65 % для S, 79 % для Se и 56 % в случае Те).

Заключение

В работе показано, что использованный нами метод расчета B3LYP/SDD дает адекватные результаты в предсказании геометрических параметров, энергий диссоциации, ИК- и Раман-спектров соединений серы, селена и теллура. Рассчитанные методами FLAPW в твердом теле и B3LYP/SDD в газовой фазе длины связи и постоянные решетки халькогенидов свинца достаточно близки к экспериментальным значениям в сульфиде свинца. Проведен анализ ковалентной и ионной составляющих связей свинец-халькоген. Показано, что в газовой фазе и твердом теле больший вклад вносит ковалентная составляющая, уменьшающаяся от селена к теллуру.

Рецензенты:

Жерин И.И., д.х.н., профессор кафедры «Химическая технология редких, рассеянных и радиоактивных элементов» Физико-технического института Томского политехнического университета, г. Томск;

Ковалева С.В., д.х.н., профессор кафедры Томского государственного педагогического университета, г. Томск.

Работа поступила в редакцию 24.06.2014.

Scientific journal
Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

QUANTUM-CHEMICAL STUDY OF STRUCTURE AND PROPERTIES OF THE LEAD HALCOGENIDES

Fundamental research
Scientific journal | ISSN 1812-7339 | Certificate - PI №77-15598