Устройства с вращающимся рабочим органом (барабанные машины, шнековые устройства, ленточные грануляторы и т. д.) широко используются в химической промышленности. При этом рабочей средой является твердый дисперсный материал, обладающий связностью и подчиняющийся закону внутреннего трения Кулона. Целью настоящего исследования является описание движения дисперсных материалов в устройствах с вращающимся рабочим органом.
В работе [1] для описания движения твердой дисперсной среды во вращающемся барабане было предложено использовать тензор напряжений, который учитывает внутреннее трение в соответствии с законом Кулона. Главным недостатком предложенного подхода является несимметричность тензора напряжений, что противоречит условию изотропности среды, и отсутствие учета связности. Этих недостатков лишен тензор напряжений, представленный в виде
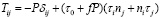, (1)
где P – среднее нормальное напряжение; τ0 – связность среды; τi, nj – единичные векторы касательной и нормали к линии тока; δij– символ Кронекера.
Уравнение движения сплошной среды в напряжениях записывается в виде
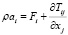, (2)
где ρ – плотность среды; Fi – вектор объемных сил; ai - вектор ускорения; xi – вектор координат. Подставляя выражение (1) в уравнение (2), получим уравнения движения в форме Эйлера:
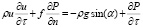, (3)
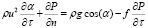, (4)
где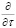 
,
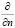– производные в направлении соответственно касательной и нормали к линии тока; u – модуль скорости в точке среды; a – угол между вектором скорости и осью Ох, которая расположена горизонтально; f – коэффициент внутреннего трения.
Система уравнений (3)-(4) дополняется уравнением неразрывности, которое может быть записано в форме Эйлера:
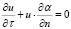. (5)
Система уравнений (3)-(5) является системой уравнений в частных производных первого порядка. Для ее решения необходимо постановка четырех граничных условий, которые во многом определяют способ решения задачи.
Рассмотрим на примере движения сыпучего материала во вращающемся цилиндре. В работах [2, 3] указывается, что при движении сыпучего материала во вращающемся цилиндре в режиме переката, существуют две области различного поведения материала: в области, непосредственно примыкающей к стенке цилиндра (область I), проскальзывание между слоями сыпучего материала отсутствует; в верхней области (область II) имеет место проскальзывание слоев сыпучего материала. Общая граница областей при малых скоростях вращения цилиндра может быть представлена в виде плоскости, параллельной поверхности естественного откоса сыпучего материала в неподвижном цилиндре. Расчетная схема представлена на рис. 1.
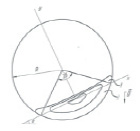
Рис. 1. Расчетная схема движения дисперсного материла во вращающемся цилиндре
В выбранной системе координат система уравнений (3)-(4) для области II может быть приведена к виду:
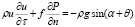, (6)
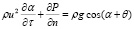. (7)
При получении уравнений (6),(7) предполагается, что величины поверхностных сил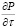 
и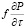 
малы по сравнению с проекциями силы тяжести. Система уравнений (5),(6) полностью совпадает с уравнениями, приведенными в работе [3].
Система уравнений (6),(7) может быть приведена к одному уравнению и записана в более удобных для решения переменных:
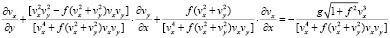, (8)
где vx и vy соответственно проекции вектора скорости на координатные оси в выбранной системе координат.
Уравнение (8) замыкается уравнением неразрывности:
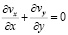. (9)
Граничные условия для системы уравнений (8),(9) составляются из условия, что в области I сыпучий материал движется как
твердое тело и записываются в виде:
; 
; 
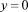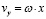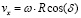, (10)
где w – угловая скорость вращения цилиндра; R – радиус цилиндра; 2 δ – угол загрузки материала в цилиндре.
Для численного решения системы уравнений (8), (9) с граничными условиями (10) использовался стандартный метод сеток [4]. В соответствии с этим методом значения координат определяются формулами:
; 
; 
; 
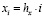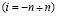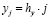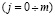; (11)
где hx, hy – соответственно шаги интегрирования по координатам x и y; n и m соответственно число точек сетки.
Выполним следующие преобразования:
; 
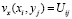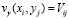. (12)
Тогда частные производные заменяются приближенными значениями:
; 
; 
; 
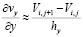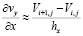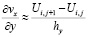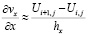. (13)
В соответствии с выражениями (11)-(13) система уравнений (8), (9) приводится к виду
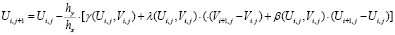, (14)
где
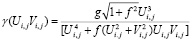; (15)
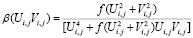; (16)
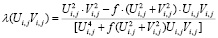; (17)
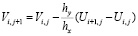. (18)
Уравнение (14) имеет особенность при значении Uij = 0. Это соответствует физике задачи, поскольку данная точка является точкой поворота. Устранение данной особенности производилось стандартным для метода сеток способом [4].
На рис. 2 представлены расчетные зависимости проекции скорости vx от координаты y. Они хорошо согласуются с экспериментальными данными, представленными авторами в более ранней работе [3].
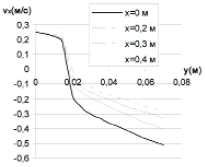
Рис. 2. Распределение скоростей дисперсной среды во вращающемся барабане R = 0,4; 2 δ = 120 °; w = 1,1 рад/с; f = 0,57. 1 – x = 0; 2 – x = 0,2 м; 3 – x = 0,3 м; 4 – x = 0,4 м
Представленные данные хорошо согласуются с экспериментальными данными, представленными авторами в более ранней работе [3].
Используя полученное распределение скоростей, определим уравнение свободной поверхности материала в области II исходя из равенства расходов в областях I и II.
Расход материала в некотором сечении, определяемым координатой x, записывается в виде
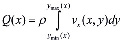, (19)
где ρ – плотность материала; ymin(x), ymax(x) –соответственно минимальное и максимальное значение координаты y в сечении.
В области I материал совершает вращательное движение и в выбранной системе координат проекция скорости vx определяется выражением:
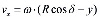. (20)
Для сечения с заданной координатой x для величин ymin(x), ymax(x) в области I получим:
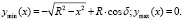(21)
Для сечения с заданной координатой x для величин ymin(x), ymax(x) в области II получим:
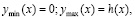(22)
где h(x) – уравнение свободной поверхности.
С учетом формул (19) – (22) в результате получим:
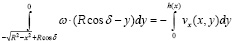, (23)
где vx (x, y) – проекция вектора скорости в области II, которая определяется из решения уравнения (14). На рис 3. представлена общая картина движения сыпучего материала. Свободная поверхность рассчитана в соответствии с уравнением (23) и близка к реальной картине движения [2].
Решена известная задача в новой постановке. Использован более простой численный метод, позволивший получить решение с хорошей точностью. Полученные данные хорошо согласуются с экспериментальными данными, представленными авторами в более ранних работах.
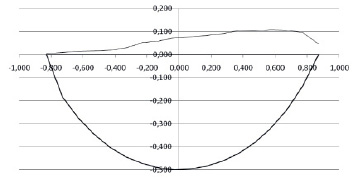
Рис. 3. Общая картина движения сыпучего материла во вращающемся цилиндре ω = 1,0 рад/с; R = 1 м; 2 δ = 120 °
Рецензенты:
Бачурин В.И., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Ярославского филиала МИИТ, г. Ярославль;
Гвоздев А.А., д.ф.-м.н., доцент Ярославского государственного университета им. П.Г. Демидова, г. Ярославль.
Работа поступила в редакцию 24.06.2014.