Теоретические и экспериментальные исследования в области электродинамики анизотропных магнитодиэлектрических сред представляют большой интерес и с точки зрения развития теории, и с точки зрения возможностей широкого практического применения подобных сред в микроволновой электронике, в тонкопленочной и интегральной оптике, акустооптике и т.д. [5, 8]. В частности, представляет определенный интерес изучение отражения поперечно-электрических (ТЕ) и поперечно-магнитных (ТМ) электромагнитных волн от левой границы и прохождения от правой границы анизотропной магнитодиэлектрической пластины, помещенной в волновод.
Постановка задачи и волновые уравнения
Пусть в регулярный волновод произвольного поперечного сечения, ось которого совпадает с осью oz некоторой декартовой системы координат, помещена анизотропная магнитодиэлектрическая пластина толщины 2d (–d ≥ z ≥ d). Рассмотрим распространение ТЕ и ТМ сигнальных волн с единичной амплитудой и частотой ω0 в подобном волноводе, предполагая, что они падают на пластину со стороны z ≤ –d (рис. 1).
Пусть диэлектрическая и магнитная проницаемости пластины имеют вид

 (1)
(1)
где ε1, ε2, μ1, μ2 – постоянные. ТЕ и ТМ поля в волноводе, как и в работах [1–4] и [9], будем описывать с помощью продольных Фурье-компонент магнитного и электрического векторов 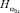 и
и 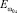 соответственно. Волновые уравнения для
соответственно. Волновые уравнения для 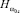 и
и 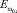 получаются из уравнений Максвелла и в различных областях волновода представляются в следующем виде:
получаются из уравнений Максвелла и в различных областях волновода представляются в следующем виде:
Для ТЕ поля:
в областях I и III (z ≤ –d и z ≥ d):
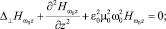 (2)
(2)
в области II (–d ≥ z ≥ d):
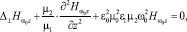 (3)
(3)
где 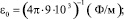
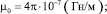
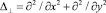 – двумерный оператор Лапласа.
– двумерный оператор Лапласа.
Для ТМ поля:
в областях I и III (z ≤ –d и z ≥ d):
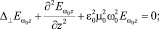 (4)
(4)
в области II ((–d ≥ z ≥ d):
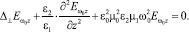 (5)
(5)
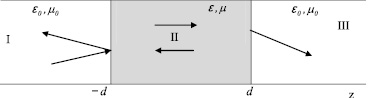
Рис. 1. Геометрия поперечного сечения волновода
Решения волновых уравнений (2)–(5) будем искать в виде равномерно и абсолютно сходящихся рядов [7] (приложение к главе 7):
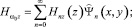
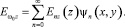 (6)
(6)
В (6) 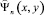 и Ψn(x, y) представляют собственные функции второй и первой краевых задач для поперечного сечения волновода и соответствуют собственным значениям
и Ψn(x, y) представляют собственные функции второй и первой краевых задач для поперечного сечения волновода и соответствуют собственным значениям 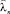 и λn. Эти функции удовлетворяют следующим уравнениям Гельмгольца с соответствующими граничными условиями:
и λn. Эти функции удовлетворяют следующим уравнениям Гельмгольца с соответствующими граничными условиями:
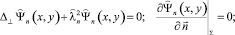 (7)
(7)
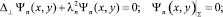 (8)
(8)
где Σ – контур поперечного сечения волновода,  – нормаль к Σ.
– нормаль к Σ.
Поперечные составляющие  и
и  ТЕ и ТМ полей, как следует из уравнений Максвелла в случае отсутствия зарядов и токов в среде [6], будут выражаться формулами:
ТЕ и ТМ полей, как следует из уравнений Максвелла в случае отсутствия зарядов и токов в среде [6], будут выражаться формулами:
Для ТЕ поля:
в I и III областях (z ≤ –d и z ≥ d):
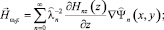 (9)
(9)
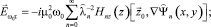 (10)
(10)
в области II ((–d ≥ z ≥ d):
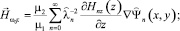 (11)
(11)
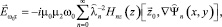 (12)
(12)
где индекс τ означает поперечные составляющие,  – орт оси oz, ∇ – оператор Набла.
– орт оси oz, ∇ – оператор Набла.
Для ТМ поля:
в I и III областях (z ≤ –d и z ≥ d):
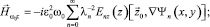 (13)
(13)
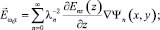 (14)
(14)
в области II ((–d ≥ z ≥ d):
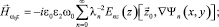 (15)
(15)
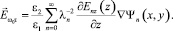 (16)
(16)
Коэффициенты отражения и прохождения по мощности.
Подставляя (6) в уравнения (2)–(5) и учитывая (7) и (8), для определения Hn(z) и En(z) в различных областях волновода, получим следующие обыкновенные дифференциальные уравнения второго порядка:
Для ТЕ поля:
в I и III областях (z ≤ –d и z ≥ d):
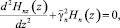 (17)
(17)
где 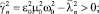
в области II ((–d ≥ z ≥ d):
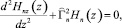 (18)
(18)
где 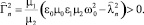
Для ТМ поля:
в I и III областях (z ≤ –d и z ≥ d):
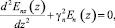 (19)
(19)
где 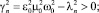
в области II ((–d ≥ z ≥ d):
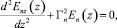 (20)
(20)
где 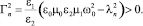
Решения уравнений (17)–(20) имеют вид:
Для ТЕ поля:
в I области (z ≤ –d):
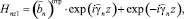 (21)
(21)
в III области (z ≥ d):
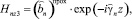 (22)
(22)
в области II ((–d ≥ z ≥ d):
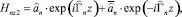 (23)
(23)
где 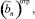
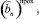
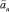 и
и  пока неизвестные коэффициенты.
пока неизвестные коэффициенты.
Для ТМ поля:
в I области (z ≤ –d):
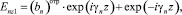 (24)
(24)
в III области (z ≥ d):
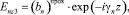 (25)
(25)
в области II ((–d ≥ z ≥ d):
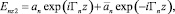 (26)
(26)
где 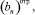
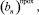 an и
an и 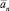 пока неизвестные коэффициенты.
пока неизвестные коэффициенты.
Все неизвестные коэффициенты можно найти с помощью следующих граничных условий при z = ±d:
Для ТЕ поля:
z = –d; 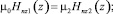
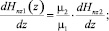 (27)
(27)
z = d; 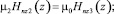
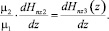 (28)
(28)
Для ТM поля:
z = –d; 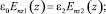
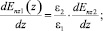 (29)
(29)
z = d; 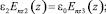
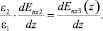 (30)
(30)
Подставляя (21)–(26) в граничные условия (27)–(30) и решая полученную систему уравнений, получим обобщенные формулы Френеля для анизотропной магнитодиэлектрической пластины в виде:
Для ТЕ поля:
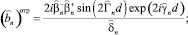
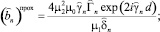 (31)
(31)
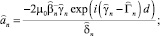
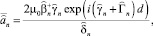 (32)
(32)
где
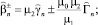
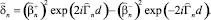 (33)
(33)
Для ТМ поля:
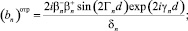
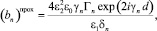 (34)
(34)
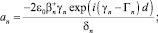
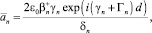 (35)
(35)
где
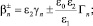
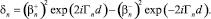 (36)
(36)
Теперь с помощью (31) и (34) можно найти коэффициенты отражения и прохождения по мощности для ТЕ и ТМ полей. Вычисления приводят к следующим выражениям:
Для ТЕ поля:
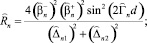
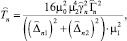 (37)
(37)
где
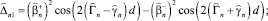 (38)
(38)
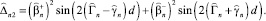 (39)
(39)
Для ТМ поля:
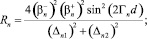
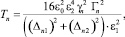 (40)
(40)
где
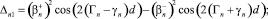 (41)
(41)
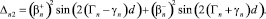 (42)
(42)
Зависимости коэффициентов отражения по мощности 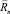 и Rn от d приведены на рис. 2–5. Графики построены согласно формулам (37)–(42) с помощью программы Mathcad при различных значениях параметров, характеризующих взаимодействие ТЕ и ТМ волн с анизотропной магнитодиэлектрической пластиной в волноводе. Как видно из рисунков, коэффициенты отражения по мощности имеют колебательный характер в зависимости от d. При увеличении ε1 в случае ТЕ волны и μ1 в случае ТМ волны максимумы коэффициентов отражения перемещаются в сторону меньших d. Огибающие максимумов в зависимости от d являются убывающими функциями. Характер зависимости коэффициентов прохождения по мощности одинаков для ТЕ и ТМ волн. При увеличении d они стремятся к нулю.
и Rn от d приведены на рис. 2–5. Графики построены согласно формулам (37)–(42) с помощью программы Mathcad при различных значениях параметров, характеризующих взаимодействие ТЕ и ТМ волн с анизотропной магнитодиэлектрической пластиной в волноводе. Как видно из рисунков, коэффициенты отражения по мощности имеют колебательный характер в зависимости от d. При увеличении ε1 в случае ТЕ волны и μ1 в случае ТМ волны максимумы коэффициентов отражения перемещаются в сторону меньших d. Огибающие максимумов в зависимости от d являются убывающими функциями. Характер зависимости коэффициентов прохождения по мощности одинаков для ТЕ и ТМ волн. При увеличении d они стремятся к нулю.
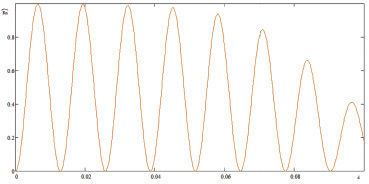
Рис. 2. Зависимость 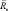 от d при ε1 = 2,5; μ1 = 350; μ2 = 14;
от d при ε1 = 2,5; μ1 = 350; μ2 = 14; 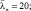 ωo = 1,2·106
ωo = 1,2·106
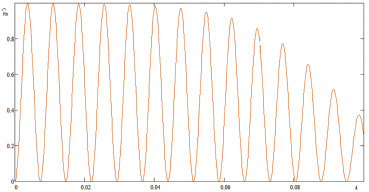
Рис. 3. Зависимость 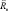 от d при ε1 = 5; μ1 = 350; μ2 = 40;
от d при ε1 = 5; μ1 = 350; μ2 = 40;  ωo = 1,2·106
ωo = 1,2·106
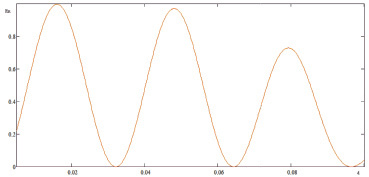
Рис. 4. Зависимость Rn от d при ε1 = 2,5; ε2 = 3; μ1 = 60; 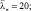 ωo = 1,2·106
ωo = 1,2·106
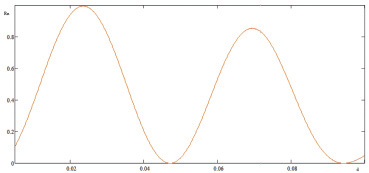
Рис. 5. Зависимость Rn от d при ε1 = 2,5; ε2 = 2; μ1 = 30; 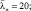 ωo = 1,2·106
ωo = 1,2·106
Теперь рассмотрим частный случай, когда длина волны в пластине много больше толщины пластины (случай «тонкой» пластины), то есть
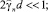
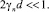 (43)
(43)
Считая, что одновременно с (43) выполняются и условия
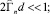
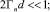
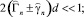
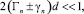 (44)
(44)
и разлагая выражения (37)–(40) в ряд Тейлора по степеням d, ограничиваясь членами, содержащими d2, получим
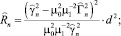
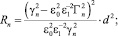 (45)
(45)
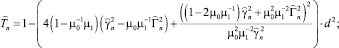 (46)
(46)
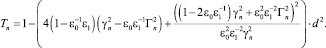 (47)
(47)
При d = 0 из (45)–(47) получим:  Rn = 0;
Rn = 0;  Tn = 1.
Tn = 1.
Заключение
В заключение отметим, что полученные в настоящей работе результаты дают возможность решить задачу излучения заряженной частицы, движущейся равномерно вдоль или перпендикулярно оси волновода, где помещена анизотропная магнитодиэлектрическая пластина толщины 2d. Отметим, что с математической точки зрения задача сводится к решению неоднородных дифференциальных уравнений.
Подобная постановка задачи представляет интерес и в плане развития теории, и в плане возможности практического применения излучения в различных областях электроники СВЧ.
Рецензенты:
Кюркчан А.Г., д.ф.-м.н., профессор, заведующий кафедрой теории вероятностей и прикладной математики Московского технического университета связи и информатики (МТУСИ), г. Москва;
Мазуров М.Е., д.ф.-м.н., доцент, профессор кафедры высшей математики Московского государственного университета экономики, статистики и информатики (МЭСИ), г. Москва.
Работа поступила в редакцию 04.06.2014.



