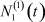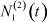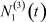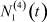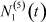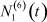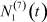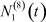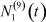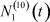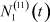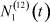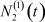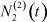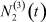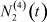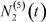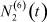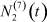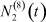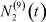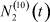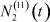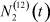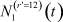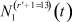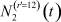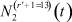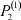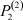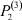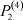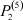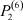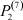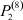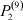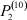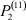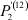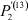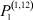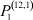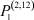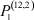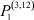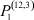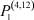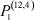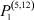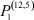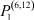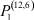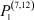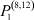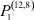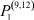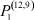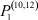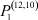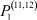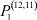Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В настоящее время значительное число исследований в экономике посвящено рынку труда. Однако достаточно общих математических моделей, описывающих этот рынок, существует немного. Одной из таких математических моделей является математическая модель самоорганизации рынка труда [1–4]. Она позволяет установить балансовые соотношения между числом работников, занятых в различных отраслях, числом потенциальных работников в этих отраслях и скоростями их изменения. В данной работе рассмотрены некоторые задачи, возникающие в рамках этой модели.

Математическая модель самоорганизации рынка труда имеет вид [1–4]:

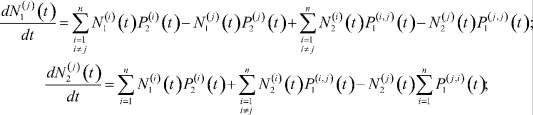(1)

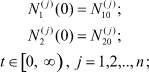
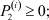
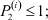i = 1, 2, ..., n; 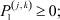j, k = 1, 2, ..., n; (2)

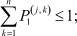j = 1, 2, ..., n. (3)

Здесь 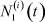– общее число работников, занятых в i-й отрасли в момент времени t; 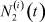– число потенциальных работников, которые могут быть привлечены для работы в i-ю отрасль и которые в момент времени t являются безработными; 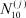, 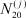– заданные числа; 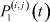– вероятность того, что безработный i-й отрасли в момент времени t может найти работу в j-й отрасли; 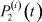– вероятность увольнения работника i-й отрасли в момент времени t.

Соотношения (1) позволяют сформулировать две задачи.

Задача 1. По заданным 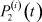, , 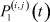, , 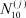, 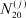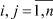определить , .

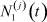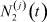Задача 1 представляет собой задачу построения решения линейной системы дифференциальных уравнений с заданными начальными условиями (задачу Коши). Эту задачу будем называть прямой задачей в рамках математической модели (1).

Задача 2. По заданным 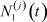, , 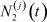, , 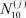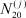j = 1, 2, ..., n, для всех t ∈ [0, ∞) определить 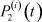, , 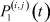i, j = 1, 2, ..., n.

Задачу 2 будем называть обратной задачей (по отношению к задаче 1) в рамках модели (1).

В прикладных исследованиях, как правило, 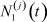, , 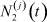j = 1, 2, ..., n, известны (заданы). Поэтому значительный интерес представляет анализ задачи 2. Её решение позволяет определить в момент t доли (вероятности) 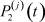, 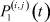работников соответственно:

а) уволенных из отрасли j;

б) перешедших из i-й отрасли в j-ю.

Цель данной работы – исследовать задачу 2 при t = 0, 1, 2, ... Время t выбирается дискретным в силу того, что измерения значени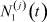й и 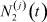возможны, как правило, только в такие моменты.

Конечно-разностный аналог задач (1) имеет вид:

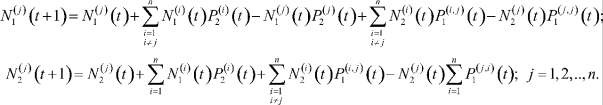(4)

Систему (4) можно переписать в векторно-матричном виде:

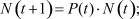(5)

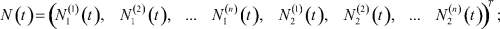t = 0, 1, 2, ... (6)

Т – операция транспонирования,

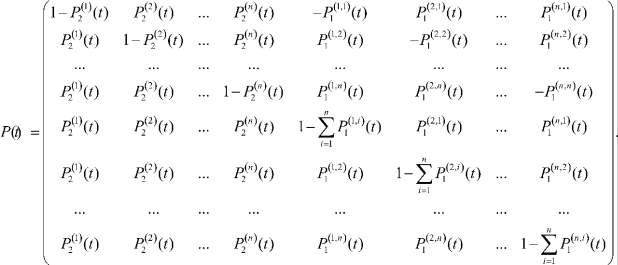(7)

Очевидно, система (4) (или, что то же самое, (5)) содержит n2 + n неизвестных 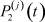, , 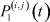где n – количество отраслей в исследуемой модели, и 2n уравнений, n ≥ 2. Так как при n ≥ 2, n2 + n > 2n, то она всегда является недоопределённой. Доопределим её.

Рассмотрим два случая: n – нечётно, n – чётно.

Пусть n – нечётно. Предположим, что на интервале [t, t + 1] элементы матрицы (7) постоянны, и на этом интервале вместо (4) (т.е. (5)) рассмотрим расширенную систему:

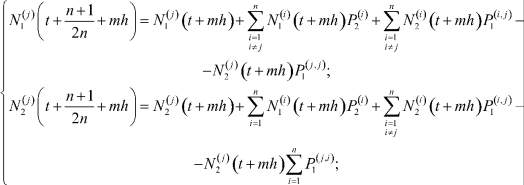(8)

j = 1, 2, ..., n;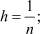

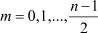
(так как по предположению n – нечётно, n ≥ 2, то 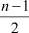– натуральное).

Значения элементов 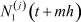, , 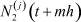, 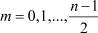при каждом j = 1, 2, ..., n в правой части (8) находим по значениям 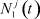, 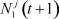и , , и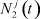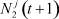спользуя формулы интерполирования

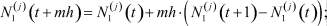
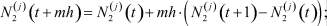(9)

j = 1, 2, ..., n; ;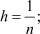

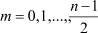значения элементов 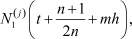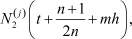j = 1, 2, ..., n, в левой части (8) находим, используя формулы

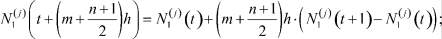
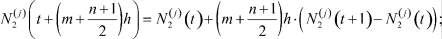(10)

j = 1, 2, ..., n; .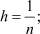

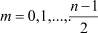Легко убедиться, что система (8) является полностью определённой: содержит 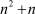уравнений и неизвестных. Её можно представить в векторно-мат- ричном виде

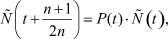(11)

где (12)

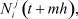
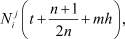
Поскольку значения 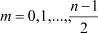, j = 1, 2, ..., n, j = 1, 2, найдены интерполированием, то они, очевидно, содержат ошибки интерполяции. Поэтому (8) целесообразно решать методом регуляризации Тихонова [5]:

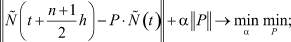α = const > 0, (13)

где α > 0 – коэффициент невязки, компоненты матрицы P (см. (7)) удовлетворяют условиям (2), (3).

Пусть n – чётно. Тогда 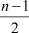(см. (8)) не является натуральным. В этом случае задачу 2 решаем в два этапа:

1. Выбираем одну из данных n отраслей, например, r-ю, r = 1, 2, ..., n, и разбиваем её на две непересекающиеся (то есть не содержащие общих элементов – работников) фиктивные подотрасли r′ и r′ + 1 таким образом, чтобы выполнялись равенства:

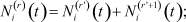
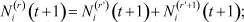
i = 1, 2. (14)

Получаем n + 1 отрасль, n + 1 – нечетно. Находим оценки вероятностей 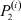, , 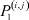i, j = 1, 2, ..., n + 1, по описанной выше схеме.

2. Объединяем отрасли r′, r′ + 1 в одну r-ю, воспользовавшись соотношениями (которые можно легко получить с помощью формулы полной вероятности и свойств условных вероятностей):

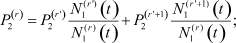
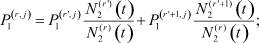j = 1, 2, ..., n + 1, j ≠ r′, r′ + 1,

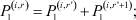i = 1, 2, ..., n + 1, i ≠ r′, r′ + 1; (15)

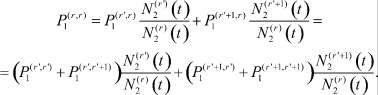
Рассмотрим следующий пример. Согласно данным Федеральной службы государственной статистики (http://www.gks.ru) отраслевая экономика России разбивается на 12 отраслей: отрасль № 1 – «Сельское и лесное хозяйство, охота, рыболовство и рыбоводство», № 2 – «Добыча полезных ископаемых», № 3 – «Обрабатывающие производства», № 4 – «Производство и распределение электроэнергии, газа и воды», № 5 – «Строительство», № 6 – «Оптовая и розничная торговля, ремонт автотранспортных средств, мотоциклов, бытовых изделий и предметов личного пользования, гостиницы и рестораны», № 7 – «Транспорт и связь», № 8 – «Финансовая деятельность, операции с недвижимым имуществом, аренда и предоставление услуг», № 9 – «Государственное управление и обеспечение военной безопасности, социальное обеспечение», № 10 – «Образование», № 11 – «Здравоохранение и предоставление социальных услуг», № 12 – «Другие виды экономической деятельности». Распределение населения по отраслям, занятого в производственном процессе в 2010–2011 гг., приведено в табл. 1 [6].

Таблица 1

Число безработных, которые могут быть привлечены для работы в каждую из указанных отраслей, оценено с помощью данных об общем числе безработных, данных о потребности организаций в работниках по видам экономической деятельности [6] и представ- лено в табл. 2.

Таблица 2

Так как число отраслей – чётное (n = 12), разобьём одну из двенадцати отраслей на две фиктивные отрасли. В качестве такой отрасли выберем «Другие виды экономической деятельности» (табл. 3).

Таблица 3

Используя (9), (10), вычислим 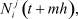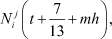m = 0, 1, 2, ..., 6, j = 1, 2, ..., 13, 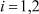, 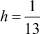и построим систему (8). Решение (8) находим методом регуляризации, используя соотношения (13), (2), (3) и средство «Поиск решений» программного продукта Microsoft Excel.

В результате проведённых расчётов находим вероятности 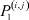(табл. 4) и вероятности 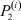(табл. 5). При этом α = 0,0001, норма выражения (13) равна 37,142 (что указывает на высокую точность полученных результатов – относительная погрешность не превосходит 0,00062).

Таблица 4

Таблица 5

Используя данные табл. 4, 5, по формулам (15) находим вероятности 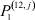, , 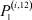, 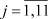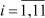(см. табл. 6), и ве- роятности

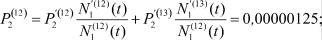
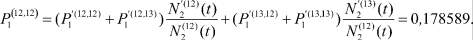
Таблица 6

Следовательно (см. табл. 5, 6), с 2011 по 2012 год вероятность увольнения из отраслей № 1, № 2, № 3, № 5, № 6, № 7, № 8, № 10, № 11 равна 0, что фактически означает отсутствие уволенных работников из данных отраслей. Значения вероятностей увольнения из других отраслей за данный промежуток времени достаточно малы – не превышают 0,01 (т.е. 1 %).

Вероятности 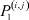– того, что безработный, уволенный из i-й отрасли, найдёт работу в j-й отрасли, максимальны в случае i = j (см. табл. 4). Это означает, что безработный, уволенный с работы в одной из отраслей в течение 2010–2011 гг. снова, как правило, был принят на работу в этой же отрасли.

Малые значения вероятностей увольнения работников из каждой отрасли и вероятностей перехода безработных из одной отрасли в другую указывают на стабильное состояние рынка труда в России в 2010–2011 гг., отсюда следует вывод о стабильности состояния экономики в эти годы: не наблюдалось ни «отмирания», ни доминирования одних отраслей над другими.

Лебедев К.А., д.ф.-м.н., профессор кафедры вычислительной математики и информатики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;

Луценко Е.В., д.э.н., профессор кафедры компьютерных технологий и систем ФГБОУ ВПО «Кубанский государственный аграрный университет», г. Краснодар.

Работа поступила в редакцию 30.04.2014.