Смесители гравитационно-пересыпного действия являются, пожалуй, наиболее распространенными устройствами, применяющимися для приготовления сыпучих смесей во многих отраслях химической, строительной, лакокрасочной промышленности, в металлургии и целом ряде других. За последние годы возможности таких устройств существенно расширились за счет разработки новых конструкций, содержащих эластичные рабочие элементы и отличающихся простотой обслуживания, малым энергопотреблением, технологичностью и низкой металлоемкостью [1–5].
Создание эффективных устройств, обеспечивающих получение сыпучих смесей высокого качества, требует разработки надежных инженерных методов проектирования и расчета, которые, в свою очередь, должны базироваться на адекватном математическом описании самого процесса смешивания. Такое описание требует изучения механики движения сыпучего материала в смесителе. Экспериментальные исследования механизмов процессов, происходящих в рабочих объемах смесительных аппаратов гравитационно-пересыпного действия, позволяют установить в объёме перерабатываемого материала наличие двух областей характерного поведения (рис. 1): транспортирования 1, где смешивания практически не происходит, и активного смешивания (обрушения) 2. Частицы, двигаясь из области транспортирования, пересекают поверхность раздела и попадают в область 2, после чего вновь возвращаются в область транспортирования.
Наибольшую сложность представляет моделирование движения материала в области активного смешивания. В работах [1, 4, 6] эта область рассматривалась как бесконечно тонкая, и анализ движения материала в ней сводился к изучению поверхностного потока. Такое упрощение уже при небольших скоростях движения частиц приводит к расхождению результатов расчета процесса смешивания с экспериментальными данными. В данной работе рассматривается механика движения сыпучего материала в слое активного смешивания, имеющего конечную толщину.
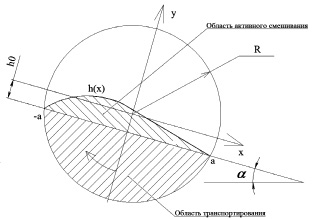
Рис. 1. Поперечное сечение барабана
Рассмотрим вращательное движение рабочей поверхности (барабана) радиуса R с угловой скоростью ω (рис. 1). Слой активного смешивания расположен над линией обрушения –а...а, расстояние до которой от центра окружности равно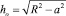 
, h(x) – функция, определяющая форму области активного смешивания; α – угол обрушения, 
, 
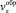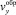– проекции скоростей частиц в области активного смешивания на оси x и y соответственно. Неизвестные h(x), 
, 
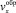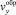можно определить исходя из следующих рассуждений.
В транспортирующей области материал движется как твердое тело. В этой области проекции скоростей частиц на оси координат имеют вид:
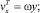(1)
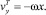(2)
На линии обрушения проекция скорости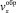 
терпит разрыв, поэтому граничное условие для нее можно записать в виде:
(3)
Если плотность сыпучего материала при переходе из транспортирующей области в область активного смешивания меняется несущественно, то проекция скорости, перпендикулярная линии обрушения, должна быть непрерывной, т.е.
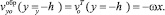(4)
Рассмотрим элемент области активного смешивания на отрезке линии обрушения (x, x + Δx) (рис. 2) и, считая плотность сыпучего материала постоянной и равной единице, запишем уравнение, выражающее закон сохранения массы:
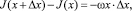(5)
где J(x) – поток сыпучих компонентов через сечение х.
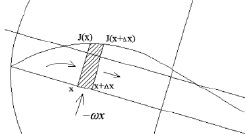
Рис. 2. Слой обрушения
Из выражения (5) при Δx → 0, следует дифференциальное уравнение:
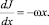(6)
Поток J(x) связан с компонентой скорости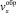 
соотношением:
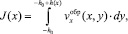(7)
где интегрирование ведется по сечению области активного смешивания. Кроме того, в этой области должно выполняться уравнение непрерывности:
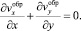(8)
Законы сохранения (6), (7) и (8) позволяют выразить две из искомых величин h(x) и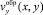 
через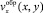 
. Сама же проекция скорости 
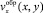должна быть найдена из уравнений движения сыпучего материала в области активного смешивания, полученных методами механики сплошной среды. Поскольку запись и анализ этих уравнений для сыпучей среды представляют существенные трудности, воспользуемся для нахождения 
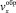упрощенной моделью. Будем считать, что в тонком слое над линией обрушения движение сыпучей среды аналогично движению вязкой жидкости в пограничном слое у твердой поверхности, то есть скорость 
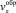линейно растет по мере удаления от линии обрушения. Тогда, с учетом (3), скорость 
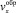можно приближенно представить в виде:
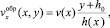(9)
где v(x) – проекция на ось x скорости частиц на свободной поверхности. На поверхности сыпучей среды влияние вязкости мало, и ускорение частицы вдоль оси x определяется только силой тяжести:
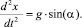(10)
Интегрирование уравнения (10) с начальными условиями x(t = 0) = –a и v(t = 0) = 0 дает:
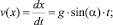(11)
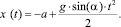(12)
Исключая из (11), (12) время t, получаем выражение для скорости частицы на поверхности как функции координаты x:
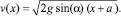(13)
Подстановка (13) в формулу (9) дает окончательное выражение для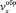 
:
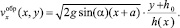(14)
Для определения h(x) вычислим поток материала через сечение x (7) с учетом (14):
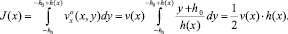(15)
С другой стороны, решение уравнения (6) с граничным условием J(–a) = 0 дает следующее выражение для J(x) [6]:
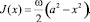(16)
Из (15) и (16) получаем уравнение для определения h(x)
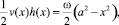(17)
из которого, принимая во внимание (13), следует:
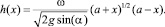(18)
Зависимость формы свободной поверхности (18) от угловой скорости ω в безразмерных координатах показана на рис. 3. При x → –a зависимость h(x) имеет параболический вид. Как видно из (18),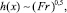 
где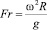 
– число Фруда для данной задачи.
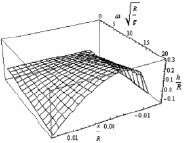
Рис. 3. Изменение формы зоны смешивания в зависимости от окружной скорости
Подстановка в уравнение непрерывности (8) выражения для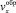 
(14) приводит к дифференциальному уравнению для компоненты скорости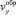 
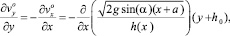(19)
интегрирование которого дает:
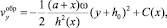(20)
где C(x) – произвольная функция, которая определяется из граничного условия (4). Окончательное выражение для проекции скорости частицы в слое обрушения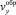 
имеет вид:
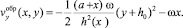(21)
Для расчета поля скоростей в области активного смешивания по формулам (14), (18), (21) необходимо определить полудлину линии обрушения a. Ее можно найти из условия сохранения объема смеси, приходящегося на единицу длины барабана:
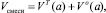(22)
где VT(a) – объем области транспортирования; Vобр(a) – объем области активного смешивания. Величина VT(a) равна площади кругового сегмента
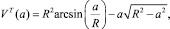(23)
а Vобр(a) определяется интегралом:
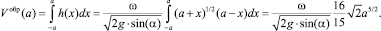(24)
При коэффициенте загрузки q объем смеси 
. Тогда уравнение (22) с учетом (23) и (24) принимает вид:
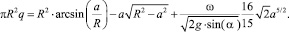(25)
Уравнение (25) позволяет определить параметр а с помощью стандартных численных методов.
Рис. 4. Сравнение расчета и эксперимента
При экспериментальных исследованиях движения сыпучего материала осуществлялась фотосъемка смеси семян чечевицы и проса (средние диаметры частиц которых составляли 3,5 и 2,5 мм соответственно) в барабанном смесителе радиусом R = 115 мм. По фотографиям определялось положение свободной поверхности циркулирующих сыпучих компонентов, а также граница областей их характерного поведения. На рис. 4 показана фотография поперечного сечения барабанного смесителя, вращающегося с угловой скоростью ω = 4 рад/с. На нее нанесены экспериментальная (1) и расчетная (2) линии свободной поверхности, а также линии раздела областей характерного поведения (пунктиром). Сопоставление линий 1 и 2 свидетельствует об их удовлетворительном совпадении в верхней части зоны активного смешивания. Наблюдаемые расхождения объясняются тем, что в предлагаемой модели не учитываются характерные для сыпучих сред эффекты локальной неравновесности, приводящие к наличию в этих средах конечных касательных напряжений при отсутствии сдвига слоев, которые и обуславливают сложную форму линии обрушения. Вместе с тем, как показывают результаты натурных и численных экспериментов, описание процесса смешивания сыпучих материалов на основе данной простой модели движения оказывается более адекватным, чем описание этого процесса без учета структуры поля скоростей в области активного смешивания [1, 4, 6].
Таким образом, в работе проведено исследование движения сыпучего материала в смесителе гравитационно-пересыпного действия, определена форма его свободной поверхности и найдено поле скоростей частиц. Полученные результаты могут быть использованы для построения математических моделей процессов смешивания, необходимых для разработки надежных методов инженерного расчета смесителей гравитационно-пересыпного действия.
Рецензенты:
Бачурин В.И., д.ф.-м.н., профессор, Ярославский филиал Московского института инженеров транспорта (университет), г. Ярославль;
Мурашов А.А., д.т.н., профессор, Ярославский филиал Московской финансово-юридической академии, г. Ярославль.
Работа поступила в редакцию 21.03.2014.