Наиболее распространенной моделью, позволяющей оценить возможность банкротства предприятия, является модель Альтмана ( – модель) которая применительно к экономике США имеет вид [5]:
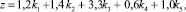 (1)
(1)
где k1 = собственный оборотный капитал/сумма активов; k2 = нераспределенная прибыль/сумма активов; k3 = прибыль до уплаты процентов/сумма активов; k4 = рыночная стоимость собственного капитала/заемный капитал; k5 = объем продаж/сумма активов:
• при 0 ≤ z ≤ 1,8 вероятность банкротства предприятия p ∈ [0,8; 1],
• при 1,81 ≤ z ≤ 2,77 p ∈ [0,35; 0,5],
• при 2,8 ≤ z ≤ 2,99 p ∈ [0,15; 0,2],
• при z ≥ 3 вероятность банкротства предприятия p незначительна (достаточно мала) и p → 0 при z → ∞.
В модели (1) параметры k1, ..., k5 не могут быть измерены точно. Поэтому в оценке значений z неизбежно появляются оценки возможности банкротства: «очень высокая», «средняя», «возможна», «маленькая». Следовательно, модель (1) порождает нечеткие множества, которым принадлежат значения величины z, а значения функций принадлежности этих множеств совпадают с вероятностями банкротства предприятия.
Цель данной работы – используя аппарат теории нечетких множеств и модель Альтмана (1) разработать методику оценки возможности банкротства предприятия.
В настоящее время нечеткие множества активно используются на практике при анализе рисков банкротства предприятий [3]. Новизна данной работы – впервые методика оценки меры нечеткости множеств использована при анализе показателей, влияющих (согласно модели Альтмана) на платежеспособность рассматриваемых предприятий.
Лингвистическая переменная
Лингвистическая переменная Ω определяется набором [1, 3]:
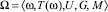 (2)
(2)
где ω – название переменной; T(ω) – терм-множество, т.е. множество имен значений ω. При этом каждому имени соответствует нечеткое подмножество X, определенное на универсальном множестве U, на котором задана переменная u, G – синтаксическое правило, порождающее T, M – семантическое правило, ставящее в соответствие каждому элементу T(ω) нечеткое подмножество X ∈ U.
При оценке кредитоспособности предприятия с помощью z-модели определим лингвистическую переменную Ω как «возможность банкротства предприятия». Синтаксическое правило G, налагаемое на переменную Ω, определим набором {высокая, средняя, небольшая, маленькая}. Тогда полное терм-множество значений T имеет вид:

Функция принадлежности
Функция принадлежности μA(u) – это функция, областью определения которой является носитель U, u ∈ U, а областью значений – единичный интервал [0; 1] [2, 3, 4]. Чем больше значение μA(u), тем выше оценивается степень принадлежности элемента носителя U нечеткому множеству A. В нашем случае в качестве носителя выберем U = {X, p, p ∈ R, 0 ≤ p ≤ 1}, где p – вероятность банкротства предприятия, соответствующая значению z, найденного с помощью уравнения (1). На этом носителе определим функции принадлежности: для значения p1 – , p2 – , p3 – , p4 – , причем первая из них отвечает нечеткому подмножеству X1, вторая – X2, третья – X3 а четвертая – X4, где X1– «возможность банкротства высокая»; X2– «возможность банкротства средняя»; X3 – «возможность банкротства небольшая»; X4– «возможность банкротства маленькая».
Будем предполагать, что функции принадлежности подмножеств X1, X2, X3, X4 имеют вид (см. также рисунок, на котором представлены функции принадлежности 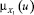 ,
, 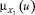 ,
, 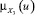 ,
, 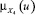 нечетких подмножеств «возможность банкротства предприятия», соответствующих X1, X2, X3, X4):
нечетких подмножеств «возможность банкротства предприятия», соответствующих X1, X2, X3, X4):
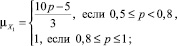 (3)
(3)
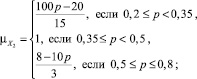 (4)
(4)
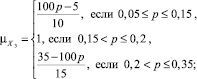 (5)
(5)
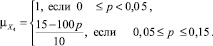 (6)
(6)
Тогда
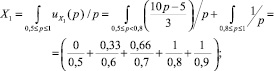 (7)
(7)
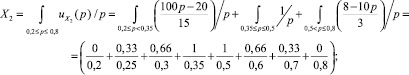 (8)
(8)
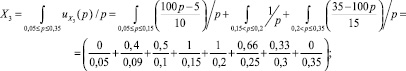 (9)
(9)
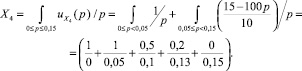 (10)
(10)
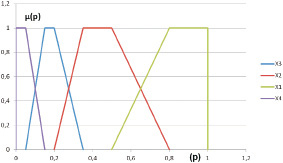
Графики функции принадлежности нечетких подмножеств X1, X2, X3, X4
Меры нечеткости множеств
Для определения степени нечёткости множества используется мера его нечёткости, сводящаяся к измерению уровня различия между нечетким множеством A и четким множеством A0, соответствующим A [3, 4].
Мера нечеткости множества A определяется как расстояние d(A) от этого множества до ближайшего к нему обычного четко заданного множества A0:
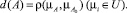 (11)
(11)
Обычным множеством, ближайшим к нечеткому A с функцией принадлежности μA(u) (μi ∈ U), называют подмножество A0 ∈ U, характеристическая функция которого имеет вид:
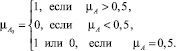 (12)
(12)
Основные обычные подмножества 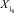 ,
,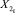 ,
, 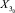 ,
, 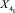 , соответственно ближайшие к X1, X2, X3 и X4, имеют вид:
, соответственно ближайшие к X1, X2, X3 и X4, имеют вид:
§ 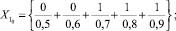
§ 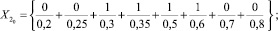
§ 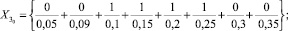
§ 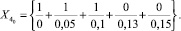
Найдем меры нечеткости определенных выше подмножеств X1, X2, X3, X4.
Вычислим меры нечеткости по линейной метрике:
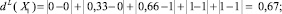
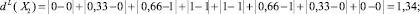
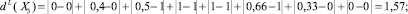
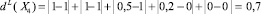
и по метрике Евклида:
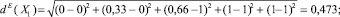
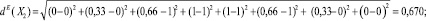
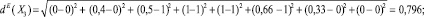
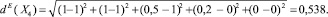
Из этих вычислений следует, что подмножество X3 является более нечетко заданным по сравнению с подмножествами X1, X2 и X4, так как меры нечеткости X3 при любой метрике больше соответствующих мер нечеткости подмножеств X1, X2 и X4.
Совершенно аналогично: X2 – более нечетко задано по сравнению с X1, X4; X4 – более нечетко задано по сравнению с X1. Пусть X > Y означает, что X более нечетко задано, чем Y. Тогда X1, X2, X3, X4 можно ранжировать следующим образом:
X3 > X2 > X4 > X1.
Следовательно, из всей совокупности {X1, X2, X3, X4} наиболее нечетко заданным является X3 – «возможность банкротства небольшая», а наименее нечетко заданным является X1 – «возможность банкротства высокая».
Рецензенты:
Попова Е.В., д.э.н, к.ф.-м.н, профессор, заведующий кафедрой информационных систем, ФГБОУ ВПО «Кубанский государственный аграрный университет», г. Краснодар;
Уртенов М.А.Х., д.ф.-м.н, профессор, заведующий кафедрой прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.
Работа поступила в редакцию 11.01.2013.



