В данной статье описан метод расчета полей деформаций и определения усилий при растяжении полосы, имеющей начальные размеры: длина – l0, ширина – a0, толщина – f0 для условия пластичности, связанного с линиями уровня поверхности деформаций [5]. Также дана сравнительная характеристика решений при плоском напряженном состоянии для различных имеющихся критериев пластичности на рис. 1: условие пластичности Мизеса (III), новое условие пластичности (IV), условие пластичности Треска (I, II).
Рассмотрим растяжение полосы с непрерывным полем скоростей перемещений. Также предположим, что захваты, обеспечивающие перемещение верхнего и нижнего концов образца, не препятствуют движению материала вдоль их оси.
Граничные условия: при y = 1, σyy = 2k; при y = –1, σyy = 2k, σxx = σxy = 0.
Данные граничные условия приводят к предположению, что весь образец находится в пластическом состоянии с однородным полем напряжений и прямолинейным полем линий скольжения, наклоненных к оси х под углом.
Поле скоростей при плоской деформации с учетом условия текучести, связанное с линиями уровня поверхности деформаций, которая имеет вид [2].
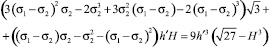
определяется системой уравнений:
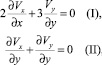. (1)
Преобразуя (1) по законам
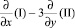и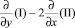 
,
получаем волновые уравнения:
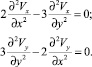(2)
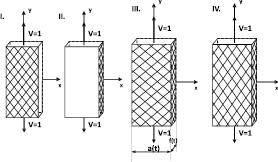
Рис. 1. Полоса: длина – l0, ширина – a0, толщина – f0. Условие пластичности Мизеса (III), новое условие пластичности (IV), условие пластичности Треска (I, II). V – скорость растяжения полосы
Общее решение системы (2) имеет вид:
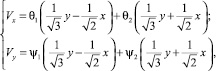(3)
где θ1, θ2, ψ1, ψ2 − произвольные дважды дифференцируемые функции.
Будем рассматривать симметричное пластическое течение с двумя осями симметрии x и y. Граничные условия для скоростей перемещений:
при x = 0 Vx = 0, при y = 0 Vy = 0,
при x = a Vx = const, при y = 1 Vy = V. (4)
Подставляя (4) в (3), имеем:
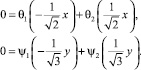
Откуда следует, что
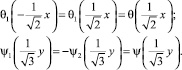(5)
При дифференцировании уравнений (3) возможно приобретение новых решений. Подставим (5) в (2):
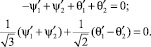(6)
Учитывая (6),
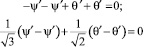, (7)
откуда следует, что ψ′ = θ′.
Пусть ψ′ = θ′ = A′, где А – некоторая дифференцируемая функция. Тогда А = θ = ψ + C, C – const. Из граничных условий (4) получим:
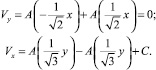(8)
Из первого равенства (8) следует, что функция A(t) нечетная, из второго – С = 0.
Общее решение системы уравнений (2) при данных граничных условиях определяется в виде
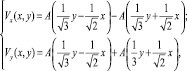(9)
где A(t) – нечетная дифференцируемая функция, удовлетворяющая граничным условиям.
Объемная плотность мощности энергии диссипации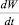 
, учитывая граничные условия, запишется в виде
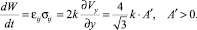
Определим вид функции A = c∙t. Тогда общий вид решения будет иметь вид:
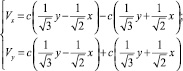(10)
при граничных условиях y = l, Vy = V из второго уравнения системы (9) следует, что
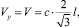
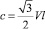
получаем:
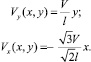(11)
Найдем:
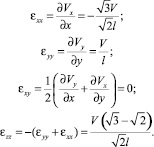
Главные значения тензора скоростей деформаций вычисляются по формулам:
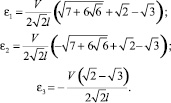
Компоненты тензоров Eij и εij связаны уравнениями
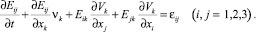(12)
В развернутом виде для случая плоского напряженного состояния [3] систему (12) можно записать в виде
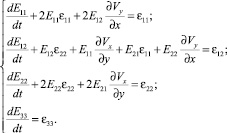(13)
Сделаем замену переменных
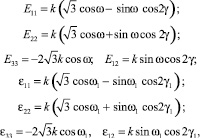(14)
где ω(x, y), ω1(x, y) – неизвестные функции, характеризующие положение точки; γ, γ1 – углы между первым главным направление и осью х. В нашем случае при одноосном растяжении в плоском напряженном состоянии нормаль к свободному контуру совпадает с одним из главных направлений и γ = γ1 = 0.
Подставим (14) в (13), получим
Получаем общее решение системы:
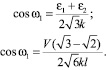
Так как l = l0 + Vt, то
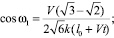(15)
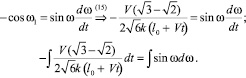
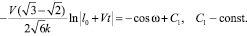(16)
Так как при ω = 0, t = 0, то
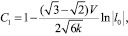
то уравнение (16) будет иметь решение
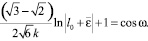(17)
Получаем значения
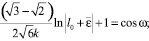
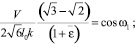
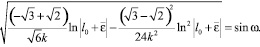
Используя записи, приведенные выше, найдем главные значения Eij:
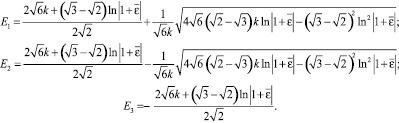(18)
Найдем связь между относительным удлинением образца и главными инвариантами Eij
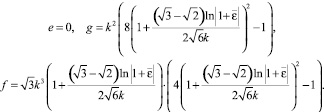(19)
Определим изменение ширины полосы а с течением времени:
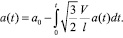
Дифференцируя по t, получим:
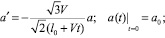
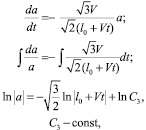
так как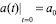 
, то 
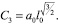
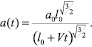(20)
Определим усилие, необходимое для растяжения полосы:
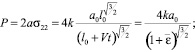
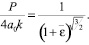(21)
Определим изменение толщины пластины с течением времени:
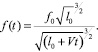
Выше была рассмотрена задача по растяжению полосы при новом условии пластичности, связанном с линиями уровня поверхности деформаций и получено решение.
При условии текучести Мизеса решение подобной задачи имеет вид:
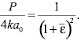
При новом условии текучести, связанном с линиями уровня тензора деформаций было получено решение (21). При решении этой задачи был найден угол между линией характеристик и осью х. Угол ψ = 50°57′[5]. В отличии от условия текучести Мизеса ψ = 54°44′
На рис. 2 представлены зависимости усилий при различных условиях текучести от деформаций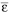 
. Коэффициенты, описывающие изменение геометрии пластин, задаются формулами:
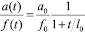– для условия пластичности Мизеса,
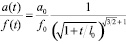– для нового условия пластичности.
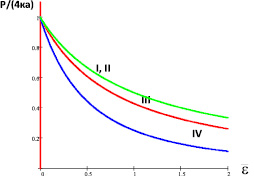
Рис. 2. Зависимости усилий от деформаций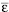 
(IV – условие пластичности Мизеса, III – новое условие пластичности, I, II – условие пластичности Треска)
При условии пластичности Треска изменяется лишь один линейный размер: либо а, либо f. Данные коэффициенты позволяют экспериментально определить выбор условия текучести для конкретного конструкционного материала. Аналогичным образом была рассмотрена задача о растяжении полосы с вырезом [1].
Рецензенты:
Амосов О.С., д.т.н., профессор, проректор по информатизации и инновациям Амурского гуманитарно-педагогического государственного университета, заведующий кафедрой информатики, г. Комсомольск-на-Амуре;
Одиноков В.И., д.т.н., профессор, директор, Институт машиноведения и металлургии Дальневосточного отделения Российской Академии наук, Хабаровский край, г. Комсомольск-на-Амуре;
Ильмушкин Г.М., д.п.н., заведующий кафедрой высшей математики, Димитровградский инженерно-технологический институт, филиал Национального исследовательского ядерного университета МИФИ.
Работа поступила в редакцию 18.06.2012.