Пульпопровод – сооружение для размещения и поддержания на плаву трубопровода, по которому производится гидротранспорт пульпы от грунтового насоса на берег (рис. 1). При создании пульпопроводов (трубопроводов) для земснарядов применяют различные материалы. Металлические трубопроводы (пульпопроводы) используются с начала становления гидромеханизации и по настоящее время [10]. Однако, в связи с большим весом, низкой износостойкостью и сложностью при монтаже, им на замену все чаще приходят современные пульпопроводы из полимерных композитных материалов (ПКМ) [8]. Слоисто-волокнистая структура материала, армирование высокопрочными и высокомодульными волокнами и тонкие стенки обеспечивают достаточно эффективное сочетание прочности, жесткости и трещиностойкости с относительно малым удельным весом. При этом следует учитывать, что распространенными элементами современных силовых конструкций (ферм, рам, балок, валов, арок, труб, трубопроводов и т.д.) являются тонкостенные пространственные стержни.
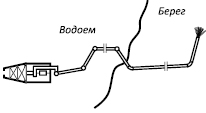
Рис. 1
Разработке теории и методов расчета тонкостенных слоистых стержней посвящен ряд работ, например [4, 5, 9]. В [4] разрешающие уравнения строятся на базе общей теории многослойных анизотропных оболочек. В работе [9] для вывода расчетных соотношений применяются вариационно-матричные методы.
1. Стержневой конечный элемент. Рассмотрим конечно-элементную модель: расчетные соотношения (матрицу жесткости и вектор узловых сил) составим, используя традиционные подходы строительной механики стержневых систем.
На рис. 2 изображен прямолинейный конечный элемент (КЭ) как участок цилиндрической оболочки. Стенка оболочки образована путем перекрестной спиральной намотки на оправку двух симметричных систем волокон (нитей или прядей). Волокна составляют с образующей цилиндра углы ± q.
Число слоев принимаем 2k + 1. Внутренний слой (оправку) считаем однородным и изотропным, слои из ПКМ (монослои) – ортотропными и линейно упругими. Связи волокон и связующего, а также отдельных слоев друг с другом предполагаем идеальными.
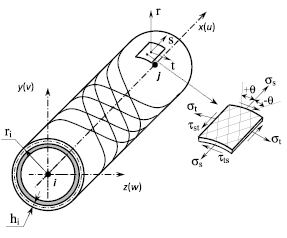
Рис. 2. Прямолинейная труба как многослойная цилиндрическая оболочка
Используем правые ортогональные системы осей координат. Координаты 1, 2, 3 (естественные координаты) связываем с осями упругой симметрии монослоя; координаты s, r, t – с его срединной поверхностью; координаты x, y, z – с осевой линией и поперечным сечением КЭ (см. рис. 2).
2. Соотношения упругости. Принимаем, что монослой «работает» в условиях плоского напряженного состояния. В этом случае зависимость между деформациями и напряжениями для однонаправленного слоя имеет вид:
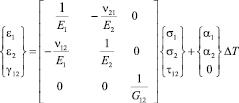(1)
или в матричной форме:
{e12} = [S0]{s12} + {a12}DТ. (1′)
Здесь {e12}, {s12}, {a12} – соответственно векторы деформаций, напряжений и коэффициентов температурного расширения; [S0] – матрица податливости; DТ – изменение температуры; Е1, Е2, G12, n12, n21, a1,
a2 – технические постоянные термоупругости (эффективные термоупругие постоянные). При этом n12E2 = n21E1.
Эффективные упругие константы определяются формулами [3]:
E1 = yE′ + (1 – y)E″;
E2 = E′E″/[yE″ + (1 – y)E′];
G12 = G′G″/[yG″ + (1 – y)G′];
n12 = yn′ + (1 – y)n″;
n21 = n12E2/E1. (2)
Формулы для эффективных коэффициентов температурного расширения имеют вид:
a1 = ya′ + (1 – y)a″;
a2 = [ya′E′ + (1 – y)a″E″]/[yE′ + (1 – y)E″]. (3)
Здесь (*)′ и (*)″ – характеристики волокна и матрицы соответственно; y – коэффициент армирования.
Соотношения, обратные (1), имеют вид:
(4)
или {s12} = [G0]{e12} – {b12}DТ,
где [G0] – матрица жесткости монослоя; {b12} – вектор температурных напряжений. Коэффициенты матрицы [G0] и вектора {b12} связаны с техническими постоянными термоупругости следующими соотношениями:
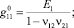
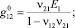
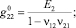
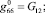
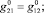
b1 = (a1 + n21a2)Е1/(1 – n12n21),
b2 = (a2 + n12a1)Е2/(1 – n12n21).
Перепишем зависимости (1) и (4) из естественной системы координат 1, 2, 3 к цилиндрическим координатам s, r, t. Получим
{est} = [S]{sst} + {ast}DТ,
{sst} = [G]{est} – {bst}DТ. (5)
Преобразования поворота осей координат относительно нормали к поверхности имеют известный вид:
[S] = [L1][S0][L1]Т; [G] = [L2][G0][L2]Т; (6)
{ast} = [L1]{a12}; {bst} = [L2]{b12}.
Здесь [L1] и [L2] – матрицы преобразований поворота:
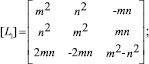
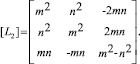(7)
При этом m = cos q, n = sin q. Индекс «т» обозначает операцию транспонирования матрицы.
Заметим, согласно (6), в произвольной системе координат s, r, t угловые деформации gst однонаправленного слоя получаются связанными с нормальными напряжениями ss и st, а линейные деформации es и et – с касательными напряжениями tst. В частном случае перекрестной спиральной симметричной намотки для системы, составленной из двух монослоев с углами ± q, коэффициенты s16 = s26 = 0, g16 = g26 = 0, ast = 0, bst = 0. В результате указанные связи исчезают.
При напряженном состоянии с компонентами: ss, tst, st = 0 технические постоянные термоупругости ортотропного композита будут равны [1]:
; 
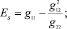
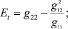
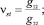
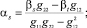
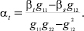(8)
3. Матрица жесткости. Матрицу жесткости КЭ представим в виде:
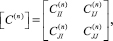(9)
где n – порядковый номер КЭ; i и j – номера узлов;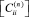 
, 
, 
, 
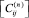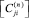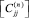– подматрицы жесткости КЭ размера (6×6).
Подматрицу жесткости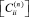 
определяем через подматрицу податливости КЭ – 
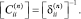. Компоненты симметричной матрицы 
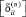находим при помощи интегралов Мора. Тогда, для консольного КЭ (считаем узел j защемлен) получим [2]:
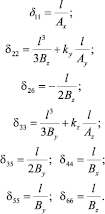(10)
Оставшиеся коэффициенты матрицы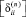 
равняются нулю. В этом случае деформированное состояние КЭ определяется шестью независимыми обобщенными координатами, образующими вектор обобщенных перемещений узла (i),
{qi} = {ui vi wi jxi jyi jzi}Т.
В формулах (10) Ax, Ay, Az, Bx, By, Bz – это жесткости поперечного сечения стержня на растяжение-сжатие, сдвиг, кручение и изгиб соответственно. Причем,
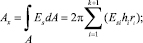
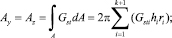(11)
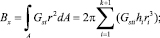
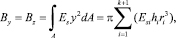
где безразмерные коэффициенты
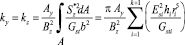(12)
учитывают неравномерное распределение по поперечному сечению касательных напряжений изгиба (определяются согласно [2] в результате осреднения энергий деформации сдвига). Здесь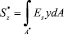 
– упруго-статический момент части поперечного сечения A*; i – порядковый номер слоя;
ri, hi – средний радиус и толщина слоя; l – длина КЭ.
Подматрицы жесткости КЭ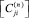 
и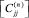 
находятся при помощи преобразований вида:
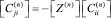
и
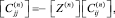(13)
где [Z(n)] – матрица линейных преобразований [6].
4. Вектор узловых сил. Распределенные температурные и гидродинамические воздействия заменяем эквивалентной системой сосредоточенных узловых сил. Для этого используем основную систему метода перемещений: узловые силы в системе координат x, y, z (рис. 2) находим как реакции узловых связей, взятые с обратным знаком,
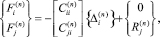(14)
где 
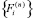и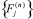 
– шестикомпонентные векторы узловых сил; 
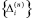– вектор упругих перемещений узла i:
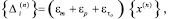
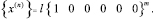(15)
Для трубы с тонкими стенками:
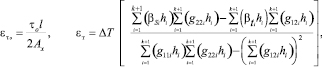
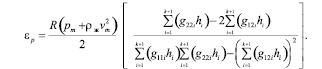(16)
Здесь рm и vm – стационарные составляющие давления и скорости внутреннего потока; rж – плотность; tо – интенсивность сил трения жидкости о стенки трубы [7];
R – радиус отверстия трубы; g11, g12, g22 – элементы матрицы (6).
Вектор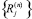 
определяет реакции в узле j от сил трения интенсивностью tо:
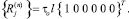
В частном случае изотропного тела формулы (16) получают известный вид:
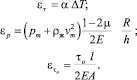(17)
Заключение
Таким образом, получены расчетные соотношения для коэффициентов матрицы жесткости и вектора узловых сил КЭ тонкостенного трубопровода, изготовленного из волокнистого композита. Рассмотрено двухкомпонентное статическое нагружение, включающее действие температуры и внутреннего давления. Учитывается слоистая структура материала и анизотропия термоупругих свойств.
Результаты получены при выполнении исследований в рамках государственного задания Минобрнауки России на выполнения НИОКР, а также гранта РФФИ № 10-08-97017-р_поволжье_а.
Рецензенты:
Савельев В.В., д.т.н., доцент, профессор кафедры строительного производства Чебоксарского политехнического института (филиал) ФГБОУ ВПО «Московский государственный открытый университет
им. В.С. Черномырдина», г. Чебоксары;
Поздеев А.Г., д.т.н., профессор, заведующий кафедрой водных ресурсов ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.
Работа поступила в редакцию 16.10.2012.