- is the impulse of power, which act on the body "m". We show that conservative forces and potential fields are not exist. The statement that 
is the statement about the existence of Perpetuum mobile of the first kind.
Показано, что формула для работы A=FsdS является частным случаем более общей формулы A= I2 / 2m, где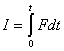 
-импульс силы, действующий на тело . Введено понятие и вычислена работа поворота. Показано, что консервативных сил и потенциальных полей не существует. Утверждение, что в потенциальном поле 
есть утверждение о существовании Perpetuum mobile I рода.
The formula of work A=FsdS is the particular case of the common formula A= I2 / 2m, where 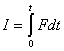- is the impulse of power, which act on the body "m". We show that conservative forces and potential fields are not exist. The statement that is the statement about the existence of Perpetuum mobile of the first kind.
Поле сил называется потенциальным, если работа при перемещении в этом поле зависит лишь от начальной и конечной точек пути и не зависит от траектории. Другим эквивалентным определением потенциальности является требование равенства работы нулю при перемещении по любому замкнутому контуру [1]. Силы, образующие такое поле, называются консервативными (потенциальными).
Работа и потенциальная энергия определяются одинаковыми выражениями, отличающимися только знаком [2].
(1a)
(1б)
где Fs - проекция силы F на направление перемещения частицы dS. Используя II закон Ньютона: 
, выражение (1а) можно представить в виде
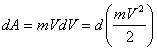или 
(1в)
где K - кинетическая энергия. Совпадение выражений (1а)-(1в) приводит к закону сохранения и превращения механической энергии, понятию консервативных сил и потенциальных полей.
Из курса термодинамики известно, что работа в газовом процессе зависит от вида процесса, а изменение внутренней энергии 
или потенциальной энергии давления 
не зависит от вида процесса, а зависит только от начального и конечного состояния системы (здесь V - объем идеального газа, P - давление, i - число степеней свободы молекул). Причина расхождений между механическими и газовыми процессами кроется в неправильности выражения (1а) и в отсутствии понятия еще одного вида работы - работы поворота.
В соответствии с законом инерции Галилея [3] всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его скорости. Это свойство тел называется инертностью. Чтобы преодолеть сопротивление, необходимо приложить усилие, т.е. совершить работу. Однако в курсах механики определены только работы для разгона тела и изменение модуля его скорости. Для этого используется теорема о кинетической энергии [3,4]: изменение кинетической энергии материальной точки при ее перемещении между двумя положениями равна работе, совершенной при этом силой: 
.
Автором [5-7] впервые была введена и рассчитана работа поворота тела массы m при постоянной скорости V0 на угол α от первоначального направления движения (поворот вектора импульса):
; 
; 
(2)
Общепринятое выражение для работы можно получить на основе II закона Ньютона 
. Умножим обе части равенства на пройденный путь S: 
. Поскольку 
, то получим 
или A=K. Отметим, что умножая обе части уравнения на S, мы тем самым отказываем в работе тем силам, которые не производят перемещение тела (S=0 ). Формула 
отказывает в работе тем силам, которые перпендикулярны к перемещению S (
), т.е. центростремительным и гироскопическим силам. Однако, автором в работах [5-7] было показано, что эти силы также совершают работу. Поэтому получим другое выражение для работы. Запишем II закон Ньютона в дифференциальной форме 
и рассмотрим задачу о разгоне первоначально неподвижного тела (трение отсутствует). Интегрируя, получим для постоянной силы: 
. В левой части 
-импульс силы, а в правой 
- импульс тела (количество движения). Возведя в квадрат и разделив на 2m обе части выражения, получим
или 
(3)
Это выражение не связано с путем , пройденным телом за время t, т.е. оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным, хотя, как утверждают во всех курсах физики, в этом случае никакой работы не совершается.
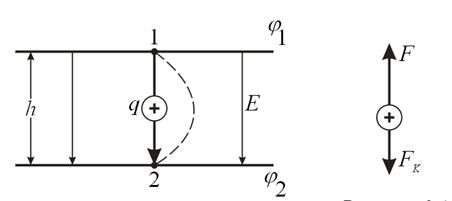
Будем рассматривать однородные потенциальные поля: поле силы тяжести вблизи поверхности Земли (рис. 1) и электростатическое поле конденсатора (рис.2), в которых движение материальной точки m или заряда q под действием сил поля происходит из точки 1 в точку 2 по вертикальной линии, параллельной силовым линиям поля (линиям напряженности g или E). По другим направлениям и траекториям они двигаться не могут. Если они движутся из т.1 в т.2 по криволинейной траектории (на рис.1 и 2 - штриховые линии), то, значит, на них еще действуют другие (сторонние) силы, которые искривляют вертикальную траекторию, на что дополнительно тратится работа поворота.
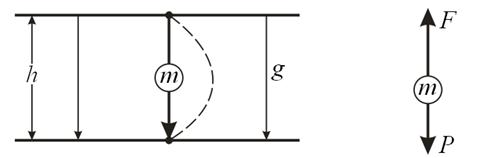
1а 1б
Рисунок 1(а, б). Поле силы тяжести вблизи поверхности Земли
2а 2б
Рисунок 2(а, б). Электростатическое поле конденсатора
Для того, чтобы заряд или материальная точка изменили движение на противоположное (движение от т.2 к т.1) необходимо приложить стороннюю силу F, направленную вертикально вверх (рис.1б и 2б).
Будем различать два вида работ. I - естественная работа, когда действуют только силы поля и движение происходит по вертикальной линии 1-2. Для гравитационного поля (рис.1) работа 
. В результате этой работы потенциальная энергия 
переходит в кинетическую 
. Для электрического поля (рис.2) (гравитационное поле отсутствует) 
, где 
, 
, 
, 
.
II - вынужденная работа - совершается сторонними силами против сил поля при движении от т.2 к т.1. Принципиальное отличие работ I и II вида состоит в том, что в I случае на тело (заряд) действует только одна сила, а во II случае действуют, как минимум, две силы. В курсе физики [3, стр.133] говорится, что «Если 
, то, проецируя это векторное уравнение на направление элементарного перемещения dS, получим 
, а после умножения на dS: 
или 
. Таким образом, элементарная работа результирующей двух или нескольких сил равна сумме элементарных работ этих сил. Очевидно, то же утверждение справедливо и для работ на конечных перемещениях: 
». Однако автор [3] ошибается: аддитивность, т.е. простое арифметическое сложение работ, выполняется только для взаимноперпендикулярных сил, например: Fx, Fy, Fz. А для сил, действующих вдоль одной оси, аддитивность работ не выполняется. Это связано с тем, что работа A пропорциональна квадрату силы F2 : т.к. 
, 
, то 
. Если взять 
, то работа 
.
Рассмотрим движение материальной точки от 2 к 1 (рис.1), возможны 3 варианта [8]. I - бросание вертикально вверх с начальной скоростью V0 за счет действия мгновенной силы в виде 
. Затраченная работа 
. II - подъем силой 
, где часть силы, равную 
, назовем силой левитации. Подъем будет происходить равноускоренно: 
, . На тело при подъеме действуют две силы: F и сила тяжести 
. 
. Умножая это выражении на t2, получим баланс импульсов, а разделив на 2m, получим баланс энергий (работ). Отдельно запишем положительную и отрицательную работы:
;
(4)
Положительную работу, совершаемую силой F, можно представить в виде:
(5)
Это выражение имеет минимум, равный 
при 
. Сумма работ A+ и A- дает величину 
, т.е. величину кинетической энергии, приобретенной телом на высоте h. Отрицательная работа , совершаемая силой тяжести при подъеме тела вверх, вовсе не равна mgh. Она равна
(6)
При большой величине избыточной силы 
, когда 
, она асимптотически стремится к величине 2mgh.
III вариант - тело находится в состоянии левитации (приложена сила 
). Для того, чтобы тело двигалось вверх, в начальный момент времени на тело действует направленный вверх единичный мгновенный импульс силы 
. При подъеме тела на высоту 
положительная работа
;
(7)
Эта работа имеет минимум, равный 
при величине 
. Отрицательная работа, совершаемая силой тяжести
(8)
При больших значениях начального импульса (
) она асимптотически стремится к своему обычному значению 
.
Рассмотрим те же три варианта возвращения заряда q [9], имеющего массу m, из т.2 в т.1 (рис.2). I вариант - действие единичной мгновенной силы в виде . Энергия, приобретенная зарядом в начале движения 
. II вариант - подъем силой , где сила левитации 
. Положительная работа
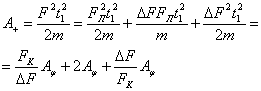(9)
где t1 определяется из соотношения: 
. Выражение (9) имеет минимум в случае 
, равный 
. Отрицательная работа кулоновской силы
(10)
При минимальной 
работа кулоновской силы 
.
III вариант - приложена сторонняя сила 
, а для перемещения заряда вверх ему сообщается единичный импульс силы 
за счет действия мгновенной силы 
. Положительная работа
;
(11)
Это выражение имеет минимум, равный 
при 
. Отрицательная работа кулоновской силы
(12)
При очень большом начальном импульсе (
) выражение (12) асимптотически стремится к «обычному» значению работы кулоновской силы 
.
Таким образом, проведенный анализ показал, что никаких фундаментальных консервативных сил и потенциальных полей в природе не существует. Эти ошибочные понятия возникли по одной простой причине, что почему-то считали, что работа подъема тела на высоту h равна mgh, т.е. равна потенциальной энергии и работе спуска. В действительности же работа подъема как минимум в два раза больше. А это означает, что не существует и закона сохранения и превращения энергии в том виде, как его обычно излагают: 
. В основе баланса энергий (работ) лежит баланс импульсов сил. Баланс энергий (работ) представляет собой не что иное, как I закон термодинамики в приложении к механическим процессам. Если, к примеру, тело перемещается с трением в горизонтальном направлении под действием горизонтальной силы F, то баланс импульсов сил:
(13)
где 
(II закон Ньютона), 
- сила деформации. (Любое тело при попытке привести его в движение упруго деформируется). Возводя в квадрат обе части равенства и разделив все на 2m, получим баланс энергий (работ).
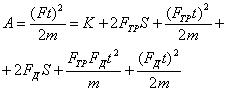(14)
где 
- путь, пройденный телом за время t. Это выражение можно рассматривать как I закон термодинамики, где в левой части 
- энергия, подводимая извне в виде импульса силы 
, а в правой части сумма энергий (работ), часть из которых, связанных с трением и деформацией, переходит во внутреннюю энергию, а - работа, затраченная на разгон тела до скорости V.
В заключение рассмотрим утверждение о том, что если в потенциальном поле материальная точка (или электрический заряд) движется по замкнутому пути, так что в результате движения точка возвращается в исходное положение, то работа, совершаемая при этом силами поля, будет равна нулю, т.е. . На наш взгляд, это есть не что иное, как утверждение о существовании Perpetuum Mobile I рода: т.е. можно перемещать тело или заряд по замкнутому пути, не затрачивая на это энергию извне (это следует из I закона термодинамики). Значит, можно построить колесо обозрения или шахтный подъемник (рис.3 а и б).
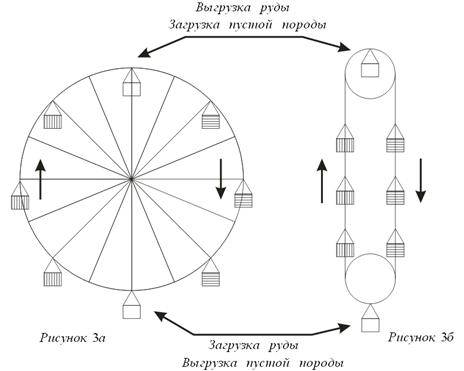
Рисунок 3(а, б). Колесо обозрения или шахтный подъемник
Например, шахтный подъемник поднимает наверх руду или уголь, а опускает такую же массу пустой породы. При идеальных подшипниках стоит только слегка раскрутить подъемник, и он будет вечно крутиться, поскольку работа подъема руды будет компенсироваться работой спуска пустой породы!
СПИСОК ЛИТЕРАТУРЫ
- Матвеев А.Н. Электричество и магнетизм. Учебное пособие. М.: Высш. школа, 1983.
- Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. Механика и молекулярная физика. М.: Наука, 1965.
- Сивухин Д.В. Общий курс физики. Том 1. Механика. М.: Наука, 1989.
- Матвеев А.Н. Механика и теория относительности: Учеб. пособие для физ. спец. вузов. М.: Высш. школа, 1986.
- Иванов Е.М. О работе центростремительных и гироскопических сил //вестник ДИТУД, №1, Димитровград, 2003.
- Иванов Е.М. Дополнительные главы классической механики. Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических сил //Успехи современного естествознания. №9, 2004.
- Иванов Е.М. Работа подъема тела в однородном поле тяжести. //Успехи современного естествознания. 2005.
- Иванов Е.М. Работа перемещения заряда в электростатическом поле. //Успехи современного естествознания. 2005.