При переработке полимерных материалов специального назначения методом экструзии очень важным технологическим параметром является температура, которая возникает в материале как за счет тепла, подводимого через корпус, так и за счет внутреннего трения. Для таких материалов верхняя граница, до которой может разогреться материал, определяется безопасностью процесса, т. к. при дальнейшем повышении температуры, начинается химическое разложение, приводящее к взрыву.
Для оценки температурных разогревов рассмотрим движение материала в канале шнек-винта, развернув его на плоскости.
Математическая постановка задачи с учетом линейной зависимости вязкости материала от температуры μ=μ0+βT имеет вид [1]
W (y) •
= a • 
+ 
(1)
(0 ≤ y ≤ h; 0 ≤ x ≤ ∞);
T(0,y)=T0; (2)
T(x,0)=T1; (3)
T(x,h)=T2, (4)
где W(y)=W0 
- профиль скорости плоскопараллельного течения (течение Куэтта); h - высота канала;m0 - вязкость среды при начальной температуре; β - коэффициент; a= 
- коэффициент температуропроводности; λ - коэффициент теплопроводности; C - теплоемкость; r - плотность; W0 - средняя скорость.
Введем следующие безразмерные переменные:
ξ = y / h; x = 
; 
= 
.
Вначале рассмотрим случай с постоянной вязкостью. С учетом принятых обозначений математическая постановка задачи приводится к виду
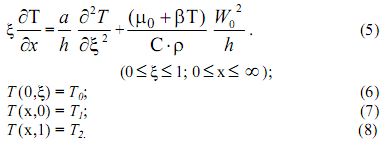
Рассмотрим первоначально случай с постоянной вязкостью μ=μ0. Решение краевой задачи (5)-(8), следуя ортогональному методу Л.В. Канторовича, в первом приближении разыскивается в виде [2],[3]
(9)
где f (x) - неизвестная функция; φ1(ξ) = (1- ξ )ξ - координатная функция.
Соотношение (9) точно удовлетворяет граничным условиям (7), (8). Неизвестную функцию f(x) найдем так, чтобы удовлетворялось уравнение (5). Для этого составим невязку уравнения (5) (полагаем, что развитие температуры в потоке жидкости происходит за счет теплоты трения, т. е. T1=T2=T0):
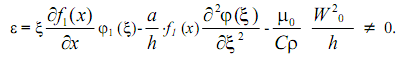
Потребуем ортогональность невязки к координатной функции φ1(ξ):
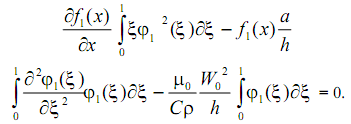
Определяя интегралы, приходим к следующему обыкновенному дифференциальному уравнению:
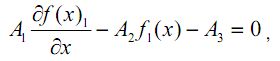, (10)
где
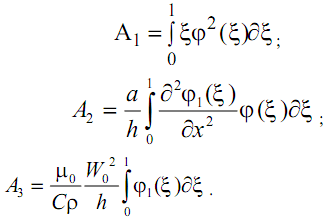. (11)
После определения интегралов уравнение (10) примет вид:
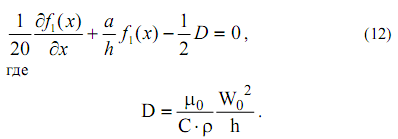, (12)
Разделяя переменные в уравнении (12), получим:
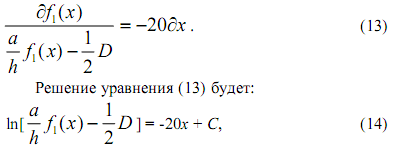
где С - постоянная интегрирования.
Для неизвестной функции f1(x) из (14) получим формулу
.
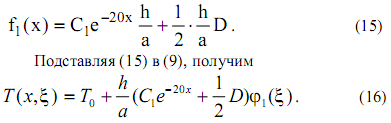Постоянная C1 находится из начального условия. Для этого составляется интеграл взвешенной невязки в начальном условии:
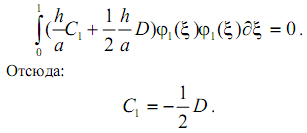
Решение задачи в первом приближении принимает вид
. (17)
Формула (17) полностью совпадает с решением в первом приближении, полученным в работе [1] путём совместного использования интегральных преобразований Лапласа и метода и Бубнова-Галеркина.
Найдём решение задачи (1), (4) для случая, когда вязкость среды является линейной функцией температуры. Составляя невязку уравнения и требуя ортогональность невязки к координатной функции φ1(ξ), получим
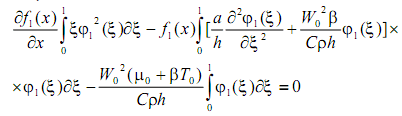
Определяя интегралы, будем иметь
.
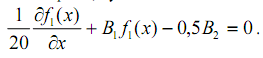где
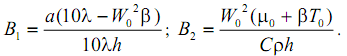
Решение последнего уравнения имеет вид
. (18)
Подставляя (18) в (9), получим
Формула для определения постоянной интегрирования С1, учитывая начальное условие (2), принимает вид
.
Решение задачи в первом приближении записывается формулой
(19)
Если положить β=0, то формула (19) полностью совпадает с формулой (17).
Найдём решение конкретной задачи теплопроводности при следующих исходных данных: r=0,05 м; h=0,02 м; a=10-7 м2/с; λ0=0,17 Вт/м К; μ0=105 Па с; W0=ωr; ω=2πn; l=2πrk=3,14 м,
где r - радиус вала экструдера; n - число оборотов вала; k - число витков вала; ω - угловая скорость.
Результаты расчётов температуры в теплоносителе экструдере представлены на графике 1. Из анализа графиков можно заключить, что температурные разогревы в канале экструдера достаточно велики и могут достигать для некоторых материалов критических значений в зависимости от оборотов шнек-винта.
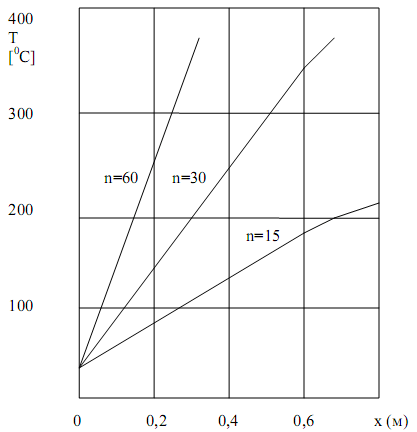
График 1. Распределения температуры в экструдере с учетом диссипации энергии
(n - число оборотов экструдера)
СПИСОК ЛИТЕРАТУРЫ
- Цой П.В. Методы расчета задач тепломассопереноса. М.: Энергоатомиздат, 1984. 423 с.
- Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. Л.: Физматгиз, 1962. 708 с.
- Кудинов В.А. Способ построения координатных систем при решении задач нестационарной теплопроводности для многослойной пластины //Изв. АН СССР. Энергетика и транспорт. 1986. № 5. С. 150-154.