Рассматриваются теоретические основы оптимального поиска пространственно нестационарных обслуживающих объектов (ПНОО). К ним также относятся мобильные лечебно-диагностические комплексы и некоторые другие.
Пусть имеется N ПНОО. Введем вектор состояний ПНОО в фиксированный момент времени:
![]() (1)
(1)
Введем множество свободных ПНОО: Θ= {i: si=1}. Рассмотрим булевы переменные (2), удовлетворяющие ограничению (3):
![]() (2)
(2)
![]() (3)
(3)
в случае обслуживания без резервирования или ограничению (4)
![]() (4)
(4)
в случае k-кратного резервирования. Резервирование может применяться в случае особо важных (сложных) вызовов, когда стоимостные показатели оказываются несущественными. Пусть далее ti - плановое время перемещения ПНОО, а gi - вероятностная компонента, зависящая от времени года, состояния трассы, объекта, метеоусловий и некоторых других факторов. Тогда задача оптимального выбора ПНОО с критерием минимизации времени ожидания формулируется для случая без резервирования как
![]() (5)
(5)
а для случая с k-кратным резервированием
![]() (6)
(6)
где τi=ti+gi - время ожидания начала обслуживания.
Задача (6) сформулирована для так называемого "мягкого" резервирования, определяемого соотношением (4) и требующим наличия в точке вызова единственного ПНОО. Однако на практике встречаются ситуации "жесткого" резервирования, например, при катастрофах, когда требуется наличие большого количества ПНОО. В такой ситуации (4) переходит в
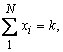 (7)
(7)
вводится среднее время ожидания обслуживания
![]() (8)
(8)
которое и необходимо минимизировать. Критерий (8) не является единственным. Например, можно потребовать, чтобы первое средство прибыло в кратчайшее время, а остальные как можно быстрее, что соответствует решению сначала задачи (5), а затем задачи (8) с (k-1)-кратным резервированием.
Заметим, что задачи (5), (6) и (8) несмотря на кажущуюся простоту не поддаются аналитическому исследованию вследствие вероятностного характера gi. Кроме того, попытки выбора ПНОО для обслуживания производятся (в соответствии с (2)) только среди свободных средств. Вместе с тем может оказаться (а на практике часто именно так и происходит), что свободное средство достаточно удалено и его ti велико, хотя вблизи от объекта, затребовавшего обслуживание, находится хотя и занятое средство, но имеющее намного меньшее ti и скоро заканчивающее обслуживание.
В связи с изложенным рассмотрим постановку задачи оперативной оптимизации назначения мобильного обслуживающего комплекса на всем множестве ПНОО.
Пусть τобс.i - ожидаемое время до окончания обслуживания i-м ПНОО. Тогда
τобс.i=tобс.i - tтек.i + gобс.i , (9)
где
tобс.i - плановое время обслуживания вызова;
tтек.i - время, прошедшее с момента начала обслуживания;
gобс.i - вероятностная компонента, зависящая от: категории обслуживаемого вызова; состояния обслуживаемой точки вызова; параметров обслуживающего ПНОО и некоторых других факторов.
При выборе на всем множестве ПНОО переопределим (2) следующим образом:
![]() (10)
(10)
Задачи (5), (6) и (8) примут следующий вид. Задача оптимального выбора ПНОО с критерием минимизации времени ожидания для случая без резервирования:
![]() (11)
(11)
Задача оптимального выбора ПНОО с критерием минимизации времени ожидания для случая с k-кратным "мягким" резервированием:
![]() (12)
(12)
Задача оптимального выбора ПНОО с критерием минимизации времени ожидания для случая с k-кратным "жестким" резервированием:
![]() (13)
(13)
Заметим, что (5) и (8), а также (11) и (13) практически идентичны за исключением различий в системах ограничений (6) и (12).
Таким образом, осуществлена постановка задачи оперативного оптимального выбора пространственно нестационарного социально-экономического объекта с критерием минимального времени прибытия к точке вызова для случаев без резервирования, с k-кратным "мягким" и "жестким" резервированием объектов.



