Рассмотрим взаимодействие двух сферических зарядов Q и q, радиусы которых много меньше расстояния между ними r0 (рис.1). заряд Q будем считать неподвижным. Сила взаимодействия между зарядами определяется законом Кулона: 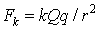 , где
, где ![]() . В случае одноименных зарядов q будет удаляться от Q. Уравнение движения будет иметь вид:
. В случае одноименных зарядов q будет удаляться от Q. Уравнение движения будет иметь вид:
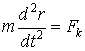 (1)
(1)
Если в точке r0 начальная скорость V0=0, то последовательно находим:
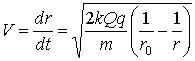 (2)
(2)
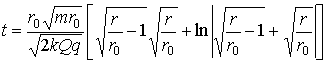 (3)
(3)
Работа перемещения q от r0 до r1 может быть определена несколькими способами:
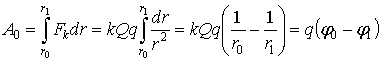 (4)
(4)
где ![]() - потенциал электрического поля. Это же выражение может быть получено на основе соотношения:
- потенциал электрического поля. Это же выражение может быть получено на основе соотношения: ![]() , где
, где ![]() - кинетическая энергия,
- кинетическая энергия, ![]() - потенциальная энергия.
- потенциальная энергия.
В работах [1-4] показано, что работу можно также вычислить, используя импульс силы ![]() :
:
![]() , где
, где 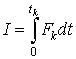 (5)
(5)
Величина dt определяется выражением (2), tk- время перемещения от r0 до r1. Интегрируя и вычисляя I2, получим то же самое выражение (4).
Чтобы переместить заряд q обратно из точки r1 в r0, необходимо приложить стороннюю силу F, большую, чем кулоновская сила Fk, и направленную в противоположную сторону.
СЛУЧАЙ I. Сторонняя сила F больше кулоновской на постоянную величину ΔF: ![]() , где
, где ![]() . Тогда уравнение движения запишется в виде:
. Тогда уравнение движения запишется в виде:
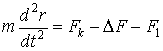 (6)
(6)
Под действием силы ΔF заряд будет совершать равноускоренное движение:
![]() ,
, ![]() .
.
Импульсы сил, действующих на тело:
![]() ,
, ![]() ,
, ![]()
где ![]() . Суммарная работа, совершаемая всеми силами:
. Суммарная работа, совершаемая всеми силами:
![]() (7)
(7)
Работа, совершаемая кулоновской силой:
![]() (8)
(8)
Работа, совершаемая сторонней силой:
![]() (9)
(9)
Отдельные составляющие работы этих сил:
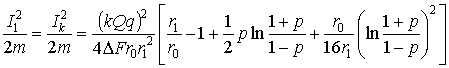 ;
;
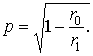
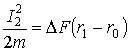 ;
; 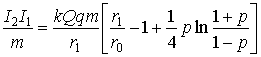
Работа ![]() имеет минимум, соответствующий значению силы:
имеет минимум, соответствующий значению силы:
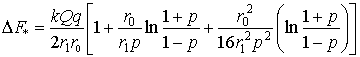 (10)
(10)
ПРИМЕР. Рассмотрим взаимодействие двух точечных зарядов (электронов): ![]() Kл;
Kл; ![]() кг;
кг; ![]() Н·м2/Кл2;
Н·м2/Кл2; ![]() м;
м; ![]() м.
м.
При свободном движении от r0 до r1 работа, определяемая выражением (4), будет равна А0 = 2,3·10-18 Дж. Сила F0 = kq2/r = 0,9216·10-7H. Для перемещения заряда в обратном направлении приложим стороннюю силу F = F1+ΔF, где ΔF=1·10-7 Н. Работа, совершаемая сторонней силой, будет равна, согласно выражению (9):
А+=(0,4015+3,02+5)·10-18=8,42·10-18Дж,
что в 3,66 раз больше А0. Работа, совершаемая кулоновской силой (8):
A-=-5,402·10-18 Дж.
Суммарная работа (7) АΣ = А- + А+ = 3,018 · 10-18Дж, как и работа А0, соответствует кинетической энергии, приобретенной зарядом после перемещения. Найдем минимальную работу А+, соответствующую силе ΔF* = 0,3527·10-7 Н, по формуле (9) А+min = (1,138 + 3,02 + 1,763) · 10-18 = 5,92 · ·10-18 Дж, что в 2,57 раз больше А0.
СЛУЧАЙ 2. Сторонняя сила больше кулоновской на некоторый постоянный коэффициент β. Тогда силы, действующие на заряд q, можно записать в виде F = Fk - F2 - F1 = Fk - βFk - F1, где F1 = |Fk|. Под действием силы F2 = βFk заряд будет совершать ускоренное движение от r1 к r0. При нулевой начальной скорости, решая уравнение движения, последовательно находим:
![]() ;
; ![]() (11)
(11)
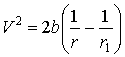 (12)
(12)
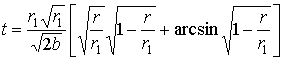 (13)
(13)
Импульсы сил при движении заряда q от r1 к r0 по модулю следующими выражениями:
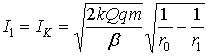 ;
; 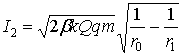 (14)
(14)
Работа сторонней силы:
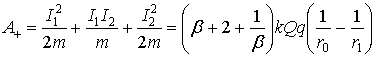 (15)
(15)
Работа кулоновской силы:
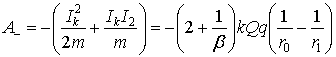 (16)
(16)
Выражение (15) имеет минимум при β=1 (рис.2):
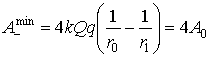 , (17)
, (17)
что в 4 раза больше работы А0 при свободном движении заряда (4). При этом работа кулоновской силы А - = -3А0. При β>>1 работа кулоновской силы стремится к минимальной величине, равной А- = - 2А0 (рис.3).
СЛУЧАЙ III. Для перемещения заряда q от r1 к r0 на него в течение некоторого времени t* (при перемещении до r* ) действует сила F по схеме, соответствующей случаю II, сообщающая заряду в точке r* кинетическую энергию:
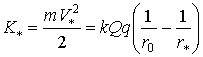 , (18)
, (18)
которая обеспечивает дальнейшее перемещение заряда q по инерции от r* к r0. Если в левую часть равенства (18) подставить квадрат скорости, определяемый выражением (12):
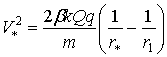 , (19)
, (19)
то можно определить искомую координату:
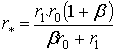 (20)
(20)
и затраченную работу:
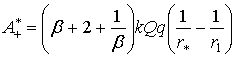
Используя данные, приведенные в рассмотренном выше примере, произведем расчет по формулам (18) - (21) для ряда значений β. Результаты сведем в таблицу 1.
Таблица 1.
|
β |
r·1010[м] |
|
|
|
1 10 100 |
0,66666 0,91666 0,990196 |
2 1,1 1,0099 |
0,5 0,9106 0,99 |
Из таблицы видно, что с ростом величины β работа сторонней силы А+, затрачиваемая на возврат заряда q из положения r1 в начальное положение r0, стремится к величине А0, определяемой выражением (4) для случая свободного движения заряда q от r0 к r1 под действием кулоновской силы. Идеальным вариантом этого случая является действие мгновенной силы, для чего следует устремит время действия силы t* → 0, а величину силы F → ∞. Тогда получим мгновенную силу в виде ![]() , где
, где ![]() - дельта-функция Дирака [5]. Единичный импульс силы будет равен
- дельта-функция Дирака [5]. Единичный импульс силы будет равен ![]() , где V1 определяется выражением (4) для случая нулевой начальной скорости V0 = 0:
, где V1 определяется выражением (4) для случая нулевой начальной скорости V0 = 0:
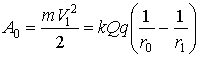
СЛУЧАЙ IV. Рассмотрим переме-щение заряда q по дуге S окружности радиуса r0. Если использовать выражение для работы (4) с использованием потенциала электрического поля As=![]() , то формально получим As = 0, так как
, то формально получим As = 0, так как ![]() , где а - начальная точка на дуге S, b - конечная точка на той же дуге. Но это неверное заключение, не работа As=0, а ЭТА РАБОТА НЕ МОЖЕТ БЫТЬ СОВЕРШЕНА СИЛАМИ ДАННОГО ПОЛЯ. Для перемещения заряда q по дуге окружности необходимо действие двух сторонних сил: удерживающей силы
, где а - начальная точка на дуге S, b - конечная точка на той же дуге. Но это неверное заключение, не работа As=0, а ЭТА РАБОТА НЕ МОЖЕТ БЫТЬ СОВЕРШЕНА СИЛАМИ ДАННОГО ПОЛЯ. Для перемещения заряда q по дуге окружности необходимо действие двух сторонних сил: удерживающей силы ![]() , которая равна, но противоположно направлена кулоновской силе, и перемещающей силе FТ, направленную по касательной. Работа постоянной перемещающей силы FТ
, которая равна, но противоположно направлена кулоновской силе, и перемещающей силе FТ, направленную по касательной. Работа постоянной перемещающей силы FТ ![]() , где t - время перемещения. Поскольку силы FT и Fу взаимно перпендикулярны, то работы этих сил аддитивны, т.е. суммарная работа
, где t - время перемещения. Поскольку силы FT и Fу взаимно перпендикулярны, то работы этих сил аддитивны, т.е. суммарная работа ![]() .
.
СПИСОК ЛИТЕРАТУРЫ:
- Иванов Е.М. Работа и энергия в классической механике и I закон термодинамики. // Фундаментальные исследования, №8,2005,с.11.
- Иванов Е.М. Работа при движении тел с трением. // Фундаментальные исследования, №6,2005,с.10.
- Иванов Е.М. Определение работы и работа силы трения. // Успехи современного естествознания, №8,23005, с.10.
- Иванов Е.М. Работа и энергия в классической механике и первый закон термодинамики. Димитровград, ДИТУД УлГТУ, 2005.
- Арсенин В.Я. Математическая физика. М.: Наука, 1966.




 , where r0
, where r0