В статьях [1,2] дано решение задачи Коши о движении материальной точки вблизи поверхности планеты без учета сопротивления атмосферы.
Это решение имеет вид:
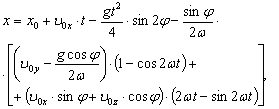 (1)
(1)
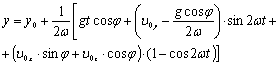 (2)
(2)
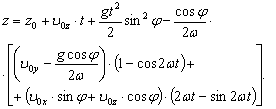 (3)
(3)
где x0, y0, z0, x, y, z - начальные и текущие координаты точки, расположенной в Северном полушарии; t - время; ω - угловая скорость планеты; φ - географическая широта; g - ускорение свободного падения, u0x, u0y, u0z - проекции начальной скорости; ось x направлена по касательной к меридиану на север, ось y - по параллели на восток, ось z - по отвесу вниз.
В тех же работах [1,2] начат анализ полученного решения. В докладе излагаются новые результаты в этом направлении. Численные расчеты по формулам (1)-(3) показали, что когда начальная скорость направлена на запад (u0y<0, u0x=u0z= 0), то точка падает по спиралеподобной траектории, поворачиваясь вправо. Сказанное справедливо для планет, направление вращения которых такое же, как у Земли.
Приводится сравнение точного решения (1)-(3) с приближенным решением, полученным в виде разложения в ряд.
Показано, что, опираясь на (1)-(3), можно сформулировать задачу нахождения оптимальной траектории точки в зависимости от величины и направления начальной скорости.
СПИСОК ЛИТЕРАТУРА
- Байрашев К.А. К задаче о влиянии вращения Земли на движение материальной точки (в печати).
- Байрашев К.А. Оценка влияния вращения планет на движение материальной точки вблизи их поверхностей (в печати).



