Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Характеристика системы

Рассмотрим систему n параболических уравнений в частных производных второго порядка.

,                          (1)

где U = (u₁,...,u_n), u_j=u_j(t,X), j=1,...,n, X=(x₁,...,x_n).

Запишем систему (1) в виде , где L(λ) - квадратная матрица, элементами которой являются линейные операторы

 при , , при i=j, ,  

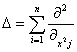
Симметричный дифференциальный оператор L, стоящий в правой части матричного уравнения , при λ<1 является сильно эллиптическим [4]. В [11] приведены результаты исследования характера разрешимости классических граничных задач для частного случая системы (1) при а=0, которая встречается в изотропной теории упругости [5]. В этом случае при λ=1 происходит вырождение типа системы, а при λ>1 эллиптический по И.Г.Петровскому оператор L не удовлетворяет условию сильной эллиптичности.

Непрерывное изменение параметра λ в области (1; +∞) осуществляет гомотопию семейства систем , зависящих от λ, к случаю эллиптической системы при λ=2 с двумя независимыми переменными, для которой классические постановки граничных задач в отдельных случаях становятся некорректными [12]. Например в [4] показано, что для системы  нарушается не только фредгольмовость, но и нётеровость первой краевой задачи Дирихле на плоскости. В частности, доказано [1,2], что для такой системы однородная задача Дирихле в любом круге имеет бесконечное множество линейно независимых решений.

Исследуем систему (1) при ненулевых значениях параметров а и λ. Практический интерес представляют решения, являющиеся суперпозицией волн с одинаковой частотой колебаний:

,       (2)

переменные амплитуды которых связаны системой 2n уравнений

,j=1,...,n, (3)

,  j=1,...,n.

Характеристической матрицей системы (3) является симметрическая клеточная матрица , в которой симметрическая матрица В при  имеет вид:

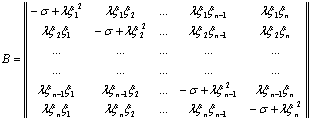
Элементарными преобразованиями матрица А приводится к форм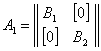е , где

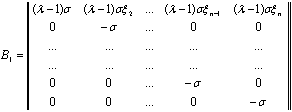
Так как матрицы А и А₁ эквивалентны, их собственные числа совпадают:

, , j=2,..., n, n+2, ..., 2n.

Следовательно, система (3) при λ<1 сильно эллиптична, при λ=1 параболически вырождается, а при λ>1 является системой гиперболического типа.

Влияние начальных условий

Обозначим  и отнесём к классу M(Rⁿ) ограниченные функции , а к М¹(Rⁿ) функции с ограниченными производными первого порядка.

Задача 1. Найти стремящиеся к нулю при t→∞ решение системы (1), удовлетворяющее начальным условиям.

,                          (4)

где все f_j - заданные в классе M¹(Rⁿ) функции.

Теорема 1.

Если λ<1, то задача 1 имеет единственное решение в классе

Доказательство: Из системы (1)

,  

для функции 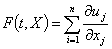 получаем уравнение

                                   (5)

с начальным условием

Последняя задача для параболического уравнения (5) при λ<1 и  имеет единственное решение в классе .

Считая далее  известной функцией, систему (1) можем представить в виде:

, .

Задача (4) для последней параболической системы имеет единственное решение в классе Q₅ [5].

Теорема 2.

Если λ>1 и , то задача 1 имеет единственное решение в классе Т.

Доказательство: При λ>1 уравнение  является уравнением параболического типа с обратным ходом времени [9]. Так как при , то из принципа максимума для параболических уравнений получаем, что в области Е переменная , следовательно, задача Коши с нулевыми начальными условиями для системы (5) будет иметь единственное решение в классе Т, отсюда вытекает, что задача 1 также корректна в этом классе.

Влияние режима на границе области

Исследуем развитие эволюционного процесса, моделью которого является система (1), в полупространстве  в момент времени, достаточно удаленный от начального, когда влияние исходного состояния настолько ослабевает, что им практически можно пренебречь и рассматривать поведение искомых функций только в зависимости от условий на границе области исследования

, ,

.

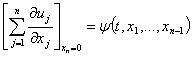Рассмотрим случай, когда граничные функции задаются в виде гармоник с нулевыми начальными фазами с одинаковой постоянной частотой и переменными амплитудами

.

Отнесем к классу Ф(Rⁿ) все функции f(X) множества С^∞(Rⁿ), убывающие при вместе со своими производными быстрее любой степени  [8], и поставим следующую задачу:

Задача 2.

В области Р найти ограниченное на бесконечности решение системы (1) в виде (2), которое будет удовлетворять граничным условиям:

, ,

 ,

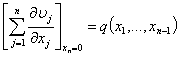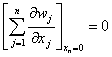,            (6)

где заданные функции q и p_j, j=1,..., n-1 принадлежат классу Ф(R^n-1).

Теорема 3.

При λ ≠1 существует единственное в классе  решение задачи 2.

Доказательство: из системы (3) для новых неизвестных:

, ,                (7)

получаем соотношения:

, , (8)

и систему:

, ,

,

,   ,

.

Характеристическая матрица системы (9) имеет вид , где:

есть диагональная матрица размерностью .

Собственные числа матрицы D равны

следовательно, система (9) при λ<1 сильно эллиптична.

Если в (n+1)-ом и (2n+2)-ом уравнении системы (9) знак в обеих частях уравнений поменять на противоположный, то система (9) будет и при λ>1 удовлетворять определению сильной эллиптичности.

Построим решения системы (8), ограниченные во всех точках полупространства  и удовлетворяющие на его границе требованиям

,      (10)

Система (8) в спектральных характеристиках преобразования Фурье по переменным

,

,

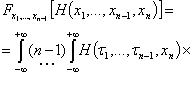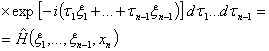
принимает вид

,          (11)

,

где

Определяя при λ≠1 ограниченные на бесконечности решения последней системы, удовлетворяющие условиям

,

,

находим

,

,

Здесь , α и β - положительные корни системы алгебраических уравнений:

,            ,

, , .

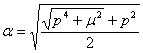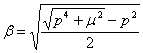Считая далее H и G известными, применим преобразование Фурье по переменным  к системе:

,  ,               (12)

,        ,

и граничным условиям (5). В спектральных характеристиках Фурье с учетом (12) получаем задачу

,

,     

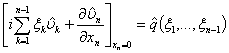,            (13)

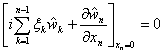
для системы

, ,

,

, ,

,

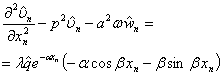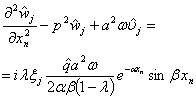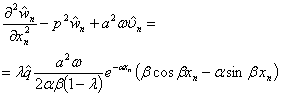которая легко деформируется к виду:

, ,

,

,

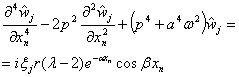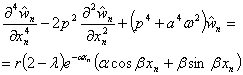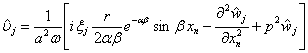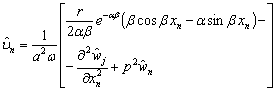,(14)

где .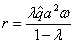

Ограниченные на бесконечности частные решения  системы линейных дифференциальных уравнений с постоянными коэффициентами (14) определяются методом подбора по виду правой части системы. С учетом граничных условий (13) с точностью до произвольных функций ,

,

,

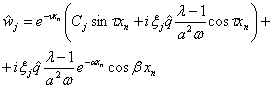где 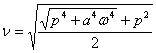, 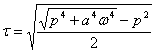- положительные корни соответствующего характеристического уравнения.

Подстановкой найденных функций  и их производных в выражениях для  из системы (14) определяются

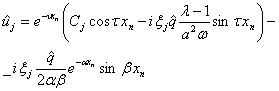
Из граничного условия (13)  получаем . Следовательно, группа решений  системы (14) определяется условиями (13) единственным образом.

Аналогичными методами находятся с точностью до произвольных функций  и  решения системы (14)         

,

.

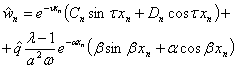Подстановкой найденных функций в граничные условия для производных (13) получаем систему для определения неизвестных C_n и D_n

,                   (15)

.

Так как главный определитель системы (15) отличен от нуля:

,

произвольные функции C_n и D_n , а, следовательно, и решение задачи 2 определяются единственным образом.

СПИСОК ЛИТЕРАТУРЫ

1. Бицадзе А.В. Об единственности решения задачи Дирихле для эллиптических уравнений с частными производными //Успехи мат.наук, 1948, т.3, N 8, с.211-212.
2. Бицадзе А.В. Краевые задачи для эллиптических уравнений второго порядка. М.: Наука, 1966.
3. Владимиров В.С. Уравнения математической физики. М.: Наука, 1976.
4. Михлин С.Г. Курс математической физики. Санкт-Петербург: Издательство «Лань», 2002.
5. Михлин С.Г. Спектр пучка операторов в теории упругости //Успехи математических наук. 1973. Т. 28-3(171). С.43-82.
6. Сергиенко Л.С. О разрешимости граничной задачи для системы уравнений в частных производных второго порядка, вырождающейся во всем пространстве. Вестник Новосибирского государственного университета. Серия: математика, механика, информатика. Т.2, вып.2, (2002), С.60-63.
7. Сергиенко Л.С. Исследование системы, обобщающей классическое уравнение теплопередачи. Вестник Иркутского Государственного Технического Университета, 2005, т.!, №3, с.142-145.
8. Сергиенко Л.С. О постановке корректных задач для вырождающихся моделей стационарных процессов, протекающих в соленоидальном поле скоростей. //Неклассические уравнения математической физики. Новосибирск: Изд-во Ин-та математики, СО РАН, 2002, с.26-230.
9. Терсенов С.А. Введение в теорию уравнений параболического типа с меняющимся направлением времени. Новосибирск: Институт математики СО АН СССР, 1982.
10. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1976.
11. Янушаускас А.И. Граничные задачи для эллиптических уравнений в частных производных и интегро-дифференциальные уравнения. Иркутск: Изд-во Иркут.ун-та, 1997
12. Янушаускас А.И. Задача о наклонной производной теории потенциала. Новосибирск: Наука, 1985.