Для тропосферы бесспорно установлено образование сульфатов в результате реакции SO
с радикалами OH
. При этом радикалы OH образуются по цепным реакциям, сопровождающим фотолиз озона. Содержание озона (O
) в тропосфере составляет 10 – 100 млрд.
. Под действием света он претерпевает превращения, образуя атомарный кислород в основном состоянии O (
P):
O 
O + O (P); (1)
где O - молекулярный кислород. Исключительно высокореакционные радикалы OH дают с SO серную кислоту:
SO + 2 OH 
HSO
; (2)
Реакции (1 – 2),имеющие кинетические кинетическими константами K
, K, подчиняются закону действующих масс. Предположим, что характерное время конвективной диффузии серной кислоты много больше, чем характерное время химической реакции образования HSO . Опишем процессы переноса в тропосфере следующей системой уравнений:
(3)
где 
, 
- концентрации озона и серной кислоты; 
, 
- скорости ветра; 
, 
- эффективные коэффициенты диффузии. Будем искать решение уравнений (3) со следующими граничными условиями :
/ 
│ x = 0 = 0; 
| y = 0 = 0; 
/ 
| x = 0 = 0; 
| y = 0 = 0; (4)
/ 
│ x = L = 0; 
| y = H = 
; 
/ | x = L = 0; 
| y = H = 
;
где L , H – характерные масштабы, 
,
- концентрация озона и серной кислоты в стратосфере. Эти масштабы показаны на рис.1.
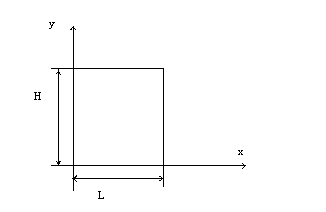
Рис. 1. Система координат и характерные масштабы.
Решение уравнений (3) будем искать методом разделения переменных:
= f (x) f(y); (5)
= f (x) f(y). (6)
Подставим выражения (5 – 6) в дифференциальные уравнения в частных производных (3), получим:
u f(y) f
(x) + 
f(x)f
(y) = 
f(y)f
(x) + 
f(x) f
(y) –
f (x) f(y); (7)
uf (y)f
(x)+
f(x)f
(y)=
f(y)f
(x)+
f (x)f
(y). (8)
Поделим уравнения (7 -8) на выражения (5 - 6) и разделим переменные:
u f
(x) -
f(x) + f (x) = 0 ; (9)
f (y) -f(y) + f (y) = 0; (10)
u f (x) -
f (x) = 0 ; (11)
f (y) -f (y) = 0; (12)
Уравнения (9 – 12) представляют собой систему обыкновенных дифференциальных уравнений. Решение этих уравнений будем искать в виде:
f (x)
exp(i
x), f(y) exp(i
y), f (x) exp(i
x), f (y) exp(i
y); (13)
где 
,
,
, 
- числа. Тогда дисперсионные соотношения будут иметь вид:
ui +
+ 
= 0 ; (14)
i
+
+ 
= 0 ; (15)
ui
+
= 0 ; (16)
i 
+
= 0; (17)
Используя краевые условия (4), получим:
= 
, n = 0, 1, 2, … (18)
= 
, k = 0, 1, 2, ... (19)
= 
, l = 0, 1, 2, ... (20)
= 
, l = 0, 1, 2, ... (21)
Учитывая соотношения (18 – 21), решения задачи записываются в виде:
= 
+ 
; (22)
= 
+ 
; (23)
где 
, 
- неопределенные коэффициенты. Для определения этих коэффициентов воспользуемся ортогональностью тригонометрических функций в расчетной области. Умножим (22) на 
, тогда:
= - 
, если n, k – нечетные; (24)
= 0, во всех других случаях.
Умножим (23) на 
, поэтому:
= - 
, если l, l - нечетные; (25)
= 0, во всех других случаях.
Озоновая дыра является примером развития событий глобального масштаба, которые разыгрываются на значительном удалении от индустриальных выбросов и ответственных за это явление источников химического загрязнения.
Исследования со спутников и самолетов показали, что над Антарктидой весной озон почти весь разрушается на уровнях 12 -13 и 25 км. Механизм разрушения озона и образования озоновых дыр представляется следующим образом. Преобладание низких температур приводит к конденсации воды и азотной кислоты и образованию «полярных стратосферных облаков». Радикалы фреонов «примерзают» к ледяным облакам; весной, когда появляется солнце, и ледяные облака нагреваются, фреоны отрываются и разрушают озон. Вследствие слабой циркуляции воздуха над Антарктидой (континент приподнят на 3 – 4 км по сравнению со средними широтами ) образуются огромные озоновые дыры. Летом приток воздуха из средних и тропических широт восстанавливает содержание озона в атмосфере. Обоснованность всей цепочки событий, приводящей к активации хлора фреонов, подтверждена измерениями, которые показали значительное увеличение концентрации «хлорина» в нижней стратосфере в холодных регионах, совпадающее с быстрым уменьшением концентрации озона.