Введение
Проектное финансирование требует принятия решений на основе долгосрочных прогнозов макроэкономических факторов. Существующие модели часто не учитывают сложные взаимосвязи между различными экономическими показателями, что приводит к значительным погрешностям при долгосрочном прогнозировании [1]. Исследование авторов стремится преодолеть эти ограничения путем разработки комплексного подхода, сочетающего методы машинного обучения с экономическими моделями. Классические регрессии и модели ARIMA показали свою ограниченность при применении к долгосрочным периодам, так как они не учитывают возможные неожиданные изменения в экономике и не позволяют адекватно смоделировать неопределенность и волатильность макроэкономических факторов [2, 3].
Основной целью исследования является разработка гибкой и масштабируемой системы прогнозирования макроэкономических показателей, способной учитывать структурные взаимосвязи между переменными и генерировать вероятностные сценарии для долгосрочного анализа рисков.
Для достижения данной цели были поставлены следующие задачи:
(1) разработать методологию отбора значимых предикторов на основе разреженных графов и алгоритма Штейнера;
(2) интегрировать регрессионные модели в систему стохастических симуляций с использованием модели CIR++ (Кокса–Ингерсолла–Росса) и метода Монте-Карло;
(3) оценить эффективность предложенного подхода на данных российской экономики, включая моделирование ВВП, инфляции и процентных ставок.
Материалы и методы исследования
Данное исследование представляет комплексный подход к построению системы прогнозирования, включающий методику отбора макроэкономических предикторов через анализ разреженных графов с их дальнейшим использованием в системе стохастических симуляций для генерации вероятностных сценариев развития экономики на основе модели CIR++ [4, 5, 6] и метода Монте-Карло для генерации сценариев таких макроэкономических показателей, как процентные ставки, индексы цен на жилье, ипотечные ставки и другие переменные, учитывая их корреляционные зависимости. Методология сочетает калибровку модели на рыночных данных, стохастическое моделирование с помесячной дискретизацией [7, 8], а также регрессионные связи между переменными, коэффициенты которых оптимально подобраны с использованием алгоритма Штейнера о минимальном дереве на разреженных графах.
В данном разделе представлена методологическая база исследования, включающая математическое обоснование и алгоритмы, используемые для отбора предикторов и построения стохастических симуляций. Используя реализацию алгоритма минимального дерева Штейнера (далее также PCST) [9] в отборе признаков [10], удается найти подграф, который максимизирует суммарный выигрыш выбранных вершин и минимизирует суммарную стоимость ребер.
1. Алгоритм находит подграф, минимизирующий функцию стоимости [11]:
,
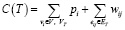где VT – множество выбранных вершин, ET – множество выбранных ребер.
Преимущество метода для отбора признаков заключается в балансе между индивидуальной значимостью признаков и их связностью, в учете структурных связей, контроле разреженности и полной интерпретируемости.
В качестве практической реализации предложенного метода использовались регрессии для прогнозирования макроэкономических показателей.
Псевдокод всего алгоритма выглядит следующим образом.
• Этап 1: отбор потенциально значимых переменных
1.1. Выбрать потенциально значимые признаки на основе экономического смысла и экспертных оценок:
1.2. Составить список признаков X_possible, которые могут влиять на целевую переменную y.
• Этап 2
2.1. Построение графа признаков G:
a. Вычислить коэффициенты корреляции Пирсона между всеми парами признаков в X_possible
b. Для каждой пары признаков (i,j):
– рассчитать вес ребра wij = 1 – |rij|, где rij – коэффициент корреляции между признаками i и j.
– если |rij| ≥ пороговое значение, добавить ребро между вершинами i и j с весом wij.
c. Создать список ребер edges = [(i, j, wij) для всех пар (i,j)].
d. Выигрыш каждой вершины (признака) pi = |riy|, где riy – корреляция признака i с целевой переменной y.
2.2. Настройка параметров алгоритма минимального дерева Штейнера (PCST)
Задать параметры алгоритма PCST:
– edges_array = массив ребер edges;
– prizes = массив выигрышей вершин pi;
– root = -1 (если корень не определен);
– num_clusters = желаемое количество кластеров;
– pruning = метод обрезки (‘strong’ или другой);
– sparsity_low и sparsity_high = границы разреженности (минимальное и максимальное количество признаков).
2.3. Применение алгоритма PCST для отбора признаков к графу G:
a. Найти подграф T, минимизирующий функцию стоимости:
C(T) = Σ (pi, для вершин не в T) +
+ Σ (wij, для ребер в T).
b. Получить отобранные признаки VT = вершины из подграфа T.
c. Сформировать новый набор признаков X_selected, содержащий только отобранные признаки Vt.
• Этап 3: Обучение модели линейной регрессии по новому методу
3.1. Инициализация:
a. Установить начальные веса коэффициентов W = нулевой вектор размерности числа признаков в X_selected
b. Задать параметры обучения:
– количество итераций num_iterations;
– массив шагов градиентного спуска steps (например, [[0.1, 0.01, 0.001], ..., повторить num_iterations раз]).
3.2. Итеративное обучение модели:
Для каждой итерации k от 1 до num_iterations:
a. Вычислить градиент функции потерь MSE:
grad = –2 * X_selected^T * (y – X_selected * W) / n
b. Обновить веса модели для каждого значения шага в steps_k:
Для каждого step_size в steps_k:
i. Обновить веса временно:
W_temp = W – step_size * grad
ii. Проекция на графовую структуру:
– Возвести элементы W_temp в квадрат:
W_squared = W_temp^2
– Применить функцию проекции на разреженность с помощью PCST:
W_proj_squared, _, _ = graph_proj_sparsity (W_squared, sparsity_low, sparsity_high, graph_opts, ...)
– Восстановить знак коэффициентов:
W_proj = sign(W_temp) * sqrt(W_proj_squared)
iii. Вычислить функцию потерь:
loss = MSE(y, X_selected * W_proj)
iv. Если loss < best_loss:
– Обновить best_loss = loss
– Обновить best_W = W_proj
c. Обновить веса модели:
W = best_W
d. При необходимости контролировать сходимость и изменять параметры обучения.
3.3. Проведение статистических тестов на обученной модели:
1. проверить значимость коэффициентов (t-тест);
2. проверить нормальность распределения остатков (тест Шапиро–Уилка или Колмогорова–Смирнова);
3. проверить гомоскедастичность остатков (тест Бройша–Пагана);
4. проверить отсутствие автокорреляции остатков (тест Дарбина–Уотсона).
• Этап 4: визуализация и анализ результатов модели:
a. построить графики реальных и предсказанных значений целевой переменной;
b. проанализировать отобранные признаки и их веса для интерпретации модели.
Результаты исследования и их обсуждение
Разработанная методология была применена к реальным макроэкономическим данным. Ниже представлена часть результатов. Процесс моделирования макропараметров осложняется сменой этапов развития экономики РФ, а также ограниченной доступностью и неоднородным качеством исторических данных. Для повышения точности и устойчивости моделей отбора признаков был применен алгоритм минимального дерева Штейнера, который позволил интегрировать как индивидуальную значимость признаков, так и их взаимосвязи.
В рамках исследования были разработаны различные модели макроэкономических показателей: инфляции индекса потребительских цен, спредов между ключевой ставкой и ставками денежного рынка, индексов цен на недвижимость и других показателей.
Особое внимание уделено модели годового роста ВВП (GDP YoY), которая имеет следующий вид:
,
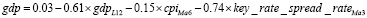где gdp – годовой рост ВВП, gdpL12 – годовой рост ВВП с лагом в 12 месяцев, cpiMa6 – скользящее среднее годовой инфляции за 6 месяцев, а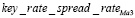 
– скользящее среднее спреда между ключевой ставкой и краткосрочной рыночной ставкой за 3 месяца. Пример визуализации регрессии для ВВП указан на рисунке 1.
На основе построенных регрессионных моделей была разработана комплексная система стохастических симуляций, архитектура которой состоит из четырех взаимосвязанных модулей:
1. Модель CIR++ для прогнозирования ставки кривой бескупонной доходности (КБД) [12].
Стохастическое моделирование процентных ставок с использованием уравнения:
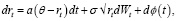
где ϕ(t) – детерминированная функция для согласования с рыночной кривой.
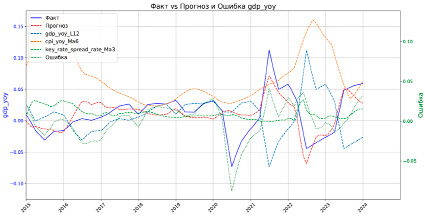
Рис. 1. Пример реализации регрессии для ВВП Источник: составлено авторами статьи
– дискретизация через модифицированную схему Эйлера:
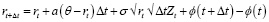
– гарантия неотрицательности ставок через ограничение на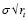 
.
2. Генерация коррелированных шоков [13]:
построение корреляционной матрицы Corr на основе исторических данных;
преобразование независимых нормальных величин Zt в коррелированные через X = L · Z, где L – нижняя треугольная матрица Холецкого.
3. Регрессионные модели для макропеременных:
для каждой переменной строится отдельная регрессионная модель, учитывающая влияние коррелированных переменных. Общий вид регрессионной модели для переменной Y может быть представлен как:
,
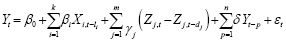где Xi,t–li – значения объясняющих переменных с лагами li, (Zj, t – Zj,t–dj) – разности значений переменных с шагом dj, Yt–p – лаговые значения самой моделируемой переменной, а εt – случайный шок, генерируемый из коррелированного нормального распределения.
4. Оркестровка симуляций:
модель CIR++ является центральным элементом системы симуляций, обеспечивая генерацию прогнозов процентных ставок с учетом их стохастической природы и динамических характеристик [14].
Для генерации распределения возможных будущих состояний каждой макроэкономической переменной используется метод Монте–Карло [15, c. 594]. Одним из ключевых аспектов реалистичного моделирования макроэкономических переменных является учет корреляций между ними, для генерации скоррелированных случайных величин в системе используется метод разложения Холецкого. Основное преимущество модели CIR++ заключается в ее способности одновременно учитывать среднелинейное возвращение ставок к долгосрочному среднему и сохранять возможность калибровки к наблюдаемой рыночной кривой доходности [16].
Финальный элемент реализации системы представляет собой модуль визуализации, который выполняет обработку и представление результатов симуляций, включая расчет статистических показателей и идентификацию различных сценариев. Примеры результатов модуля визуализации представлены на рисунке 2.
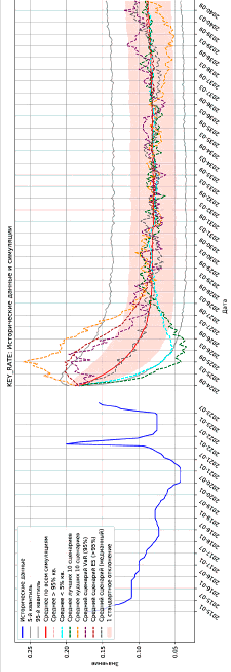
Рис. 2. Пример реализации модуля визуализации для Ключевой ставки ЦБ РФ Источник: составлено авторами статьи
Заключение
Результаты проведенного исследования демонстрируют эффективность предложенного подхода в прогнозировании макроэкономических показателей с учетом их взаимозависимостей и стохастической природы. Ключевыми преимуществами представленной системы являются ее гибкость, масштабируемость и адаптивность к различным экономическим условиям. Предлагаемый подход позволяет более адекватно оценивать риски долгосрочных проектов в сфере строительства жилой недвижимости и повышает точность финансового планирования.