Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

При анализе различных задач из финансово-экономической области возникает необходимость принятия решений в условиях неопределенности. Лицу, принимающему решение (ЛПР), для избежания грубых ошибок необходимо учитывать объективную среду, окружающую решаемую задачу. К сожалению, в момент принятия решения у ЛПР об окружающей среде может быть недостаточно информации. Во многих случаях при решении таких задач полезной оказывается математическая модель «Игра с природой», или в другой терминологии – «Статистическая игра».

Игроками в игре с природой являются игрок А – ЛПР и природа П – объективная среда. Природа абсолютно безразлична к действиям игрока А и не ставит перед собой никакой цели. Она в момент принятия решения пассивно находится в одном из своих состояний, которые принимает случайным образом. Множество всех состояний природы в игре изначально известно игроку А. Неопределенность в игре выступает в качестве отсутствия у игрока А информации о состоянии, в котором находится природа в момент принятия решения. Игрок А, будучи рациональным, стремится из возможных альтернативных стратегий выбрать наиболее эффективную.

Сравнение стратегий по их эффективности (или неэффективности) проводится по принципу оптимальности, выбираемому игроком А. Известны различные теоретико-игровые критерии, задающие принципы оптимальности, например выигрыш-критерий Вальда [2; 1, с. 273–308], риск-критерий Сэвиджа [3; 1, с. 308–349] и др. Как показывает практика принятия решений в условиях неопределенности, полезную роль играют критерии, определяющие оптимальность с совместной позиции взвешенных выигрышей и взвешенных рисков. Такие критерии будем называть синтетическими. Примерами синтетических критериев могут служить различные линейные свертки критериев Вальда и Сэвиджа [4], в том числе критерий Вальда–Сэвиджа [1, с. 652–655; 5; 6].

Цель настоящей статьи – определить новый синтетический критерий и применить его в решении финансово-экономической задачи оптимизации структуры капитала компании для максимизации ее стоимости.

Материалы и методы исследования

Пусть I ≡ {1,2,…,m}, m ≥ 2; J ≡ {1,2,…,n}, n ≥ 2. Далее, не оговаривая специально, будем рассматривать только чистые стратегии Ai i ∈ I, [1] игрока А, составляющие множество 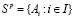(В обозначении Sp буква «p» – первая буква английского «pure» – чистый). Пусть П1,П2,…,Пn – возможные состояния природы. Числа aij, i ∈ I, j ∈ J – выигрыши игрока A в ситуации (Ai, Пj), в которой игрок А выбирает стратегию Ai, а природа пребывает в состоянии Пj. Набор выигрышей представляется в виде следующей таблицы:

называемой матрицей выигрышей, или платежной матрицей. В последней дополнительной строке таблицы (1) представлены показатели благоприятности 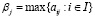, j ∈ J, состояний природы Пj, j ∈ J. Из рисков rij = βj – aij i ∈ I, j ∈ J формируется матрица рисков (2):

Из определений рисков и показателей благоприятности состояний природы следует, что все элементы матрицы (2) неотрицательны и каждый столбец матрицы (2) содержит, по меньшей мере, один нулевой риск.

Для описания нового синтетического критерия введем в рассмотрение базовое понятие синтетического выигрыша.

Синтетическим выигрышем игрока A в игровой ситуации (Ai, Пj) с выигрыш-показателем α ∈ [0,1], который будем обозначать bij(α), назовем величину

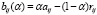, (3)

i ∈ I, j ∈ J, α ∈ [0,1].

Фигурирующий в этом определении выигрыш-показатель α ∈ [0,1] количественно выражает степень предпочтения, которое игрок A отдает выигрышам. Тогда величину 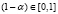можно трактовать как риск-показатель.

Как видно из определения (3), синтетические выигрыши bij(α) учитывают взвешенные с коэффициентом α выигрыши aij из платежной матрицы (1) со своими знаками и взвешенные с коэффициентом (1 – α)-риски rij из матрицы рисков (2) со знаком «минус». Из определения (3) очевидны также следующие соотношения: bij(α) ≤ αaij, i ∈ I, j ∈ J, α ∈ [0,1]; bij(0) = – rij, bij(1) = aij, i ∈ I, j ∈ J.

Используя определение рисков rij = βj – aij, i ∈ I, j ∈ J, можно получить для синтетического выигрыша (3) другие выражения, а именно:

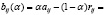
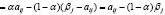. (4)

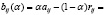
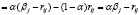. (5)

Нетрудно убедиться в том, что из выражения (4), соответственно из выражения (5) при фиксированных выигрыш-показателе α ∈ [0,1] и состоянии природы Пj, следует, что синтетический выигрыш bij(α) будет максимальным тогда и только тогда, когда максимальным будет обычный выигрыш aij, соответственно минимальным будет риск rij, т.е. равенство bij(α) = αβj эквивалентно равенству aij = βj, соответственно равенству rij = 0.

Теперь мы можем определить новый синтетический критерий, который будем называть «критерий синтетического выигрыша с выигрыш-показателем α ∈ [0,1]», или коротко – (SW)(α)-критерий (S и W – первые буквы английских synthetic – «синтетический» и win – «выигрыш»). (SW)(α)-критерий описывается следующими компонентами.

Показателем эффективности стратегии Ai, i ∈ I, по (SW)(α)-критерию, (SW)(α)-показателем стратегии Ai, который будем обозначать (SW)i(α), назовем наименьший из синтетических выигрышей (3) (или (4,), (5)) при этой стратегии:

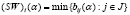, i ∈ I. (6)

Ценой игры по (SW)(α)-критерию, ((SW)(α)-ценой игры), которую будем обозначать 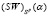, где в нижнем индексе Sp – множество чистых стратегий, назовем наибольший из (SW)(α)-показателей (6):

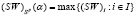. (7)

Стратегию Ai назовем оптимальной (во множестве Sp) по (SW)(α)-критерию, или (SW)(α)-оптимальной, если ее (SW)(α)-показатель наибольший среди (SW)(α)-показателей остальных стратегий. Таким образом, с учетом определения цены игры (7) стратегия Ai является (SW)(α)-оптимальной тогда и только тогда, когда ее (SW)(α)-показатель совпадает с ценой игры:

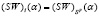. (8)

Множество (SW)(α)-оптимальных стратегий обозначим .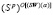

Результаты исследования и их обсуждение

В результате введения понятий выигрыш-показателя α ∈ [0,1], синтетического выигрыша (3), показателя эффективности стратегии (6), цены игры (7) и оптимальной стратегии (8) определен синтетический критерий (SW)(α).

Отметим, что (SW)(α)-критерий несравним с критерием Вальда–Сэвиджа [1, с. 652–655; 5; 6], т.е. существуют игры, в которых ни одно из множеств оптимальных стратегий по критерию Вальда–Сэвиджа и по (SW)(α)-критерию не является подмножеством другого.

Поскольку показатель эффективности (6) стратегии Ai является наименьшим синтетическим выигрышем при этой стратегии, то (SW)(α)-критерий является крайне пессимистическим (так же как и критерии Вальда, Сэвиджа и Вальда–Сэвиджа).

Рассмотрим применение (SW)(α)-критерия в оптимизации структуры капитала компании.

В настоящее время в силу неустойчивости мировой экономики все большая потребность в менеджменте возникает в использовании такого финансово-экономического показателя, как стоимость компании. Различные факторы рыночной оценки бизнеса позволяют ориентироваться на метод дисконтированных денежных потоков (ДДП) [7, с. 155], согласно которому стоимость компании обратно пропорциональна стоимости ее капитала [7, с. 157]. Весь капитал компании делится на собственный и заемный, доли которых составляют структуру капитала компании. Одним из показателей в управлении структурой капитала является средневзвешенная стоимость капитала WACC (Weight average cost of capital) :

WACC = DCK ∙ RCK + DЗK ∙ RЗK ∙ (1 – T), (9)

где DCK – доля собственного капитала, RCK – стоимость собственного капитала, DЗK – доля заемного капитала, RЗK – стоимость заемного капитала, T – ставка налога на прибыль. Показатель WACC был предложен Нобелевскими лауреатами Ф. Модильяни и М. Миллером в 1958 г. Структура капитала существенно влияет на стоимость компании. В связи с этим возникает проблема оптимальной структуризации капитала компании, которая превратилась в одну из главнейших задач финансового менеджмента.

Оптимизация структуры капитала означает обеспечение такого соотношения собственных и заемных средств, которое минимизирует средневзвешенную стоимость капитала (WACC) компании и таким образом максимизирует ее рыночную стоимость.

Известны различные подходы к выбору структуры капитала [8], однако к настоящему времени единое мнение об оптимальности структуры капитала компании так и не сложилось. В связи с этим проблема формирования оптимальной структуры капитала остается актуальной и требует дальнейших исследований.

В работах [9] и [10] подчеркнута неопределенность, связанная с влиянием внешней рыночной конъюнктуры на структуру капитала, и потому предложено для анализа проблемы оптимизации структуры капитала компании использовать математическую модель «Игра с природой». Содержание этой модели составляют: игрок A – финансовый менеджер, принимающий решения о выборе структуры капитала; стратегии Ai, i ∈ I – различные варианты структуры капитала di = (dCK / dЗK) i ∈ I, где dCK и dЗK – доли соответственно собственного и заемного капитала в i-м варианте; природа П – доходность индекса ММВБ; состояния природы Пj, j ∈ J – доходность индекса ММВБ, принадлежащего j-му интервалу (xj, xj+1), j ∈ J; выигрыши aij, i ∈ I , j ∈ J, определяются по Правилу:

aij = 1 / (1 + WACCij), (10)

где WACCij – средневзвешенная стоимость капитала при условии соответствия структуры капитала стратегии Ai и доходности индекса ММВБ, соответствующей состоянию природы Пj; зависимость выигрыша от выбранной стратегии и конкретного состояния природы определяется с помощью формулы (9) и формулы САРМ (Capital Asset Pricing Model):

САРМ = Rf + β(Rm – Rf), (11)

где Rf – доходность безрисковых активов, β – бета-коэффициент, определяющий изменение стоимости средств организации по сравнению с изменением их стоимости по всем компаниям данной отрасли, Rm – доходность рынка ценных бумаг [8].

В работе [11] данная задача рассматривается на примере ПАО «Лукойл» в рамках описанной модели, в которой dCK, dЗK ∈ [0%, 100%] и dCK + dЗK = 100%, а в роли стратегий выступает любое значение dCK ∈ [0%, 100%], принадлежащее одному из 11 промежутков (m = 11). В результате расчета числовых значений величин dCK [11] получена таблица 1 стратегий игрока A.

Природа в [11] определена как доходность из индекса ММВБ. За состояния природы Пj принимаются значения доходности ММВБ, вычисляемые на основе месячных котировок индекса с января 2015 до декабря 2017 гг., имеющиеся статистические данные делятся на n = 12 частей, и для каждой из них берется среднее значение. Таблица 2 состояний природы имеет следующий вид (табл. 2).

Выигрыши в [11] вычисляются по формуле (10) с использованием модели САРМ (11). Сформированная матрица выигрышей имеет следующий вид (табл. 3).

Таблица 1

Стратегии игрока A

Таблица 2

Состояния природы – состояния фондового рынка (в %)

Таблица 3

Сформированная матрица выигрышей

Из матрицы выигрышей видно, что стратегия A10 строго доминирует стратегию A6 и взаимно дублирующие стратегии A1 и A3, стратегия A2 строго доминирует каждую из стратегий A4, A5, A7, A8, A9, A11. Поэтому все стратегии, кроме A2 и A10, нужно удалить из рассмотрения как заведомо невыгодные для игрока A. Упрощенная таким образом матрица выигрышей получит вид:

Последняя строка матрицы (12) содержит показатели благоприятности βj состояний природы Пj , j = 1,2,3,…,12.

Используя определение риска и благоприятности состояний природы (последняя строка матрицы (12)), сформируем матрицу рисков:

Беря значения выигрышей из матрицы (12), а значения рисков – из матрицы (13), вычисляем по формуле (3) синтетические выигрыши, из которых составляем матрицу синтетических выигрышей:

Продолжение матрицы синтетических выигрышей

Продолжение матрицы синтетических выигрышей

Для синтетических выигрышей при стратегии A10 (вторая строка матрицы синтетических выигрышей) нетрудно показать, что 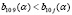, α ∈ [0,1], j = 1,2,3,…,12. Следовательно, (SW)(α)-показатель стратегии A10

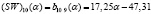, α ∈ [0,1]. (14)

Найдем (SW)(α)-показатель стратегии A2.

График каждого синтетического выигрыша b2j(α), j = 1,2,3,…,12 как функции аргумента α ∈ [0,1] является отрезком положительного наклона в полосе 0 ≤ α ≤ 1. Поэтому показатель (SW)2(α) (см. определение (6)) является нижней огибающей этих отрезков. В таблице 4 проставлены значения синтетических выигрышей b2j(α), j = 1,2,3,…,12 при α = 0 и α = 1.

Таблица 4

Значения b2j(0) и b2j(1), j = 1,2,3,…,12

Поскольку из первой, соответственно второй, строки таблицы 4:

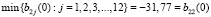. (15)

соответственно:

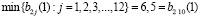, (16)

то отрезки, являющиеся графиками синтетических выигрышей b22(α) и b2 10(α), участвуют в структуре нижней огибающей.

Найдем абсциссу α* точки пересечения отрезков b22(α) и b2 10(α), для чего решим уравнение b22(α) = b2 10(α), т.е. уравнение 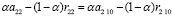, предварительно подставляя в него значения a22 и a2 10 из платежной матрицы (12), а значения r22 и r2 10 – из матрицы рисков (13). В результате получим α* = 2813 / 3168 ≈ 0,888.

В таблице 5 указаны значения синтетических выигрышей b2j(α), j = 1,2,3,…,12 при значении α = α*.

Таблица 5

Значения b2j(α*), j = 1,2,3,…,12.

Из таблицы 5:

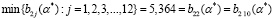. (17)

Из равенств (15), (16) и (17) следует, что показатель эффективности стратегии A2 по (SW)(α)-критерию:

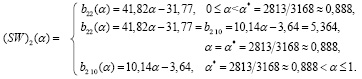(18)

Используя (14) и (18), нетрудно убедиться в том, что 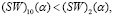0 ≤ α ≤ 1. А это говорит о том, что (SW)(α)-показатель стратегии A2 равняется цене игры. Следовательно, A2 – единственная оптимальная стратегия: 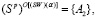α ∈ [0,1].

Итак, (SW)(α)-критерий рекомендует ЛПР при любом выигрыш-показателе α ∈ [0,1] выбрать в качестве оптимальной стратегию A2, состоящую в том, что 100% капитала компании распределяются на 69% собственного капитала и 31% заемного капитала (табл. 1). При выборе этой стратегии стоимость компании при любом состоянии фондового рынка возрастет не менее чем на 6,5% (см. платежную матрицу (12)) с риском (недостижения наибольшей стоимости компании) не более чем 31,77 %.

Заключение

В статье в играх с природой в условиях риска (т.е. с неизвестными вероятностями состояний природы) на базе введенных понятий выигрыш-показателя α ∈ [0,1] и синтетического выигрыша дается в качестве принципа оптимальности определение нового синтетического критерия, названного (SW)(α)-критерием.

Особенностью (SW)(α)-критерии является то, что он оценивает оптимальность стратегий с совместной точки зрения взвешенных выигрышей и взвешенных рисков. Более ранние известные критерии устанавливали оптимальность раздельно – либо с позиции выигрышей, либо с позиции рисков. При α = 0 (SW)(α)-критерий превращается в критерий, противоположный критерию Сэвиджа, а при α = 1 – в критерий Вальда.

Применение (SW)(α)-критерия иллюстрируется на решении задачи оптимизации структуры капитала ПАО «Лукойл» для максимизации ее стоимости.

Результаты, полученные в статье, новые и имеют теоретико-научное значение, так как привносят определенный вклад в развитие теории игр с природой. Однако (SW)(α)-критерий представляет новый подход к отысканию оптимальных стратегий при решении практических задач по принятию решений в условиях неопределенности, а потому полученные результаты имеют также и практическое значение.