Основная цель держателя портфеля заключается в понимании и достижении определенных соотношений доходности и риска для вложенного капитала. Инвестиционный портфель в простейшем случае представляет собой совокупность различных видов ценных бумаг (акции, облигации, фьючерсы и т.д.). В 1952 г. Гарри Марковиц опубликовал работу «Portfolio Selection» [1], ставшую впоследствии классикой подхода к портфельным инвестициям. На практике корректная работа с множеством инвестиционных возможностей (рассматриваемых ценных бумаг) помогает принять нужное инвестору решение. Именно такой подход и делает рынок ценных бумаг инвестиционно привлекательным и позволяет расширять круг потенциальных инвесторов, даже если результат принятого решения заранее неизвестен. Сама задача построения инвестиционного портфеля – это фактически две задачи: выбор активов из всего множества инвестиционных возможностей и последующее построение структуры, соответствующей требуемому соотношению риск/доходность [2, с. 807–815; 3, с. 588, 754].
Математические понятия и утверждения являются одним из основных инструментов для исследования области финансов и инвестиций. Метод количественных оценок, применяемый в работе, использует определения, понятия и методы теории вероятностей [4, c. 123]. Рассмотренные теоретические модели основаны на определенных в работе наборах случайных величин и случайных процессов.
Для принятия финансового решения необходимо поставить и решить две задачи. Первая – оценка стоимости, которая вычисляется определенным образом через функцию распределения доходности инвестиции. В итоге величина выражается, например, средним (или каким-либо другим параметром выборки). Вторая задача – измерение риска, для расчета которого используется дисперсия выборки. Для ее вычисления как меры риска введем далее функционал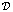 
(который опишем ниже [5, с. 451, 462]). Задача оптимизации портфеля состоит в нахождении структуры портфеля, ограниченного имеющимся бюджетом B, которая приводит к компромиссу между высокой ожидаемой доходностью и низким риском.
Материалы и методы исследования
Пусть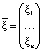 
– вектор возможных доходностей активов (случайных величин); 
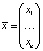– вектор, описывающий структуру портфеля (x1 + x2 +⋯+ xn = 1). Всюду далее предполагается, что инвестируется общий бюджет в размере B, а целевая доходность равна μ. Определим случайную величину, описывающую стоимость портфеля как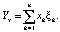 
Стандартная задача оптимизации состоит в том, чтобы минимизировать риск портфеля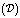 
на множестве инвестиционных возможностей X (то есть с ограничением 
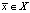), так, чтобы ожидаемая доходность от инвестирования была бы не менее целевой доходности μ. Таким образом, формализация модели выглядит следующим образом:
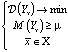
Заметим, что если функционал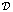 
представляет собой дисперсию (стандартное отклонение) выборки, то мы получаем хорошо известную модель Марковица.
Обозначим посредством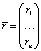 
вектор ожидаемых доходностей активов (то есть 
); 
– 
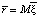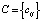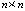ковариационную матрицу доходностей активов; (
); 
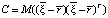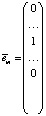– m-й единичный вектор. Поскольку стандартное отклонение является квадратным корнем из дисперсии, не имеет значения, дисперсия или стандартное отклонение рассматривается в качестве функционала, определяющего риск портфеля [3, с. 40]. Поэтому здесь и далее полагаем минимизацию функционала: 
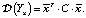При построении графиков будем использовать зависимость ожидаемой доходности от риска, где в качестве риска рассматривается стандартное отклонение. Таким образом, задача оптимизации портфеля конкретизируется:
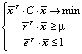(1)
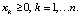
Последнее ограничение добавляется в зависимости от того, запрещены короткие продажи или нет (если нет, то не добавляется). Заметим, что это задача нелинейной, точнее, квадратической оптимизации с линейными ограничениями. Количество переменных при этом равно n. Если короткие продажи запрещены, то все переменные будут неотрицательны, а количество линейных ограничений равно двум.
Будем считать структуру портфеля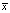 
эффективной, если она является решением системы (1) для некоторого μ.
Модель Марковица очень популярна среди оптимизационных задач портфельной теории. В основном это происходит из-за того, что она проста в использовании и сложность решения не возрастает с увеличением размера выборки. Фактически, как для теоретических моделей, так и для дискретных или выборочных моделей, все, что нужно сделать для решения задачи – это вычислить ковариационную матрицу и математическое ожидание выборки. Затем использовать эти параметры в самой модели оптимизации. Основной недостаток модели состоит в том, что дисперсия не является достаточно хорошим показателем для измерения риска (это мы покажем далее в подробном примере).
Одним из частных случаев модели Марковица является вариант, который снимает ограничения неотрицательности весов активов и имеет линейные ограничения в виде равенств
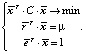(2)
Для этого случая можно найти явное решение.
Утверждение. В предположении, что матрица C обратима и вектор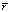 
не коллинеарен 
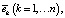оптимальное решение 
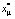задачи (2) линейно по μ и задается формулой
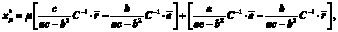
где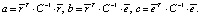 
В частности, для эффективной случайной доходности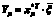 
при заданном ожидаемом доходе 
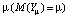риск портфеля равен
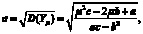
где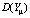 
– квадратичная функция от μ. График эффективной границы множества инвестиционных возможностей в этом случае будет иметь форму параболы.
Доказательство. Для решения задачи нелинейной оптимизации используем метод множителей Лагранжа. Лагранжиан будет иметь вид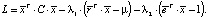 
Далее, следуя алгоритму, следует найти все частные производные и приравнять их к нулю. Найдем сначала 
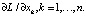Для этого сначала запишем лагранжиан в явном виде:
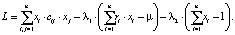
Поэтому
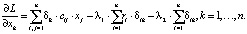
Здесь δik – символ Кронекера, следовательно:
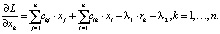
В силу того, что ковариационная матрица симметрична (ckj = cjk), последнее выражение можно записать в виде
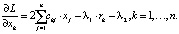
А это, в свою очередь, есть k-я компонента вектора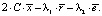 
По принципу Лагранжа этот вектор должен быть равен нулю. Двойку можно убрать, сделав замену 
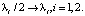Таким образом, получаем уравнение: 
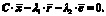Теперь найдем оставшиеся частные производные (они также должны быть равны нулю).
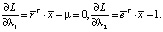
Таким образом, получаем следующую систему уравнений:
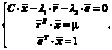
По условию ковариационная матрица является обратимой. Поэтому из первого уравнения системы находим вектор структуры портфеля:
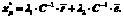(3)
Подставим это выражение во второе и третье уравнения системы. Имеем
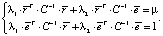
Заметим, что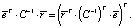 
В силу того, что это выражение является числом, а значит, совпадает с собой транспонированным, имеют место равенства
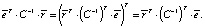(4)
Далее, поскольку ковариационная матрица является симметрической, то и обратная к ней тоже симметрическая матрица, то есть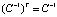 
. Значит, из (4) получаем, что 
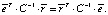Перепишем теперь систему в следующем виде:
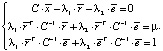
Пусть
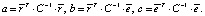(5)
Система принимает вид
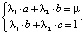
Для нахождения множителей Лагранжа λ1 и λ2 используем метод Крамера. Имеем
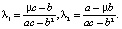
Подставляя эти значения в (3), получаем вектор структуры оптимального портфеля:
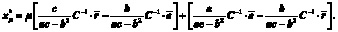(6)
Теперь найдем дисперсию оптимального портфеля. С учетом (5) и (6) имеем
+
▀
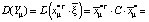
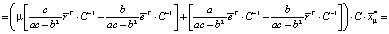
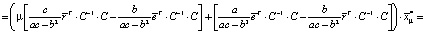
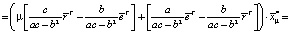
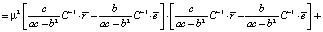
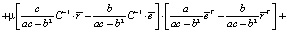
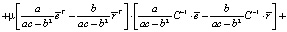
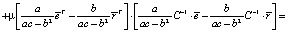
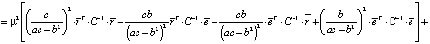
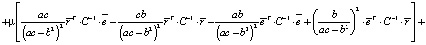
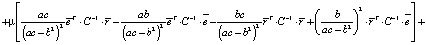
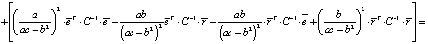
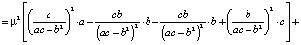
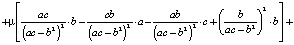
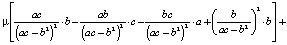
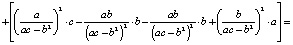
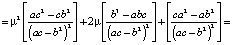
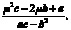Результаты исследования и их обсуждение
Для лучшего понимания результатов рассмотрим следующий реальный пример портфеля, сконструированного на базе российского рынка акций.
Пример. Рассмотрим задачу оптимизации следующего портфеля: WTCMP (ПАО «Центр международной торговли»), VGSB (Волгоградэнергосбыт), TGKA (ПАО ТГК-1), TATNP (Татнефть), SELGP (Селигдар). Вычислим основные показатели и построим эффективную границу. Исходные данные для вычислений взяты с сайта Московской Фондовой Биржи [6] (данные на 16.03.2021). Имеем основные параметры активов портфеля (таблица).
Основные параметры активов портфеля
|
Параметры активов |
WTCMP |
VGSB |
TGKA |
TATNP |
SELGP |
|
Риск |
0,3537298 |
0,9027569 |
0,3520088 |
0,4142920 |
0,4825203 |
|
Ожидаемая доходность |
0,549179468 |
0,016211624 |
0,588725112 |
0,932287324 |
0,120334357 |
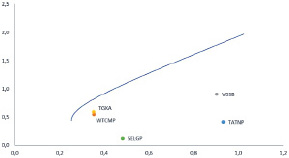
Рис. 1. Эффективная граница
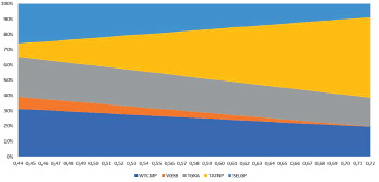
Рис. 2. Изменение долей портфеля
На рис. 1 демонстрируется, что объединение активов в портфель значительно эффективнее точечной покупки пусть и очень перспективных отдельных активов. Теперь посмотрим, какой вклад вносит тот или иной актив в рискованную составляющую портфеля (рис. 2). Теперь очевидно, что увеличение доходности портфеля достигается за счет выведения из его состава самого низкодоходного актива (Волгоградэнергосбыт), значительного снижения доли низкодоходной «Селигдар» и практически взрывного роста доли самой перспективной компании – «Татнефть» (за счет снижения всех долей всех остальных активов тоже). Соответственно, инвестору значительно проще теперь сделать выбор.
Заключение
В работе показано, что разделение инвестором выбранного уровня доходности [7, c. 421] и выбранного риска приводит к двузначной проблеме принятия решения. Однако нельзя одновременно максимизировать прибыль и минимизировать риск (поскольку одно есть функция другого). Следовательно, необходимо найти некоторый компромисс между этими целями путем фиксации одного из параметров. И далее исследовать структуру возможного портфеля для достижения приемлемого соотношения риск/доходность. Для иллюстрации на практике приведен конкретный пример, демонстрирующий набор возможных решений инвестора, а именно: при фиксированном (выбранном авторами) наборе ценных бумаг построен оптимальный портфель и исследована структура этого портфеля. Для инвестора с определенным аппетитом к риску такое прочтение задачи оптимизации портфеля является большим подспорьем при принятии решения в моменте (то есть до того, как станут известны действительные количественные показатели пары риск/доходность).