Основной математической моделью, которая применяется для планирования запасов, является так называемая классическая модель экономического размера заказа (EOQ – Economic order quantity) [1]. Данная модель описана во многих работах, в частности в книге [2]. В работе исследован вопрос минимизации суммарных издержек при управлении запасами производственного комплекса. В данной работе рассматривается задача управления запасами предприятия, состоящего из трех акционеров: складского комплекса, транспортной компании и магазина. В качестве принципа оптимальности принимается компромиссное решение управления запасами производственного комплекса при многоагентном взаимодействии акционеров [3–7].
1. Постановка задачи о нахождении компромиссного решения в моделях управления запасами производственного комплекса при многоагентном взаимодействии акционеров
В условиях рыночной экономики для производственного комплекса актуальной становится постановка задачи о минимизации суммарных издержек хранения, транспортировки запасов и издержек, связанных с заказом. При этом издержки постоянны для каждого заказа и не связаны с объемом заказа. Так же следует учитывать издержки вследствие дефицита товара. В качестве решения задачи нахождения подходящей политики работы производственного комплекса будем принимать компромиссное решение для динамической модели многоагентного взаимодействия функционирования комплекса. Рассмотрим издержки трех видов: Co – издержки выполнения заказа или затраты на подготовительно-заключительные операции; Cu – издержки хранения, приходящиеся на единицу товара; Cz – издержки вследствие дефицита, приходящиеся на единицу товара в течение единицы времени. При решении задачи нахождения оптимальной политики управления запасами получаем разные значения оптимального размера заказа. Таким образом, возникает задача нахождения подходящей политики работы предприятия.
2. Модели управления запасами производственного комплекса
2.1. Модель Уилсона управления запасами
Математические модели управления запасами (УЗ) позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара. Модель Уилсона является простейшей моделью УЗ и описывает ситуацию закупки товара, которая характеризуется следующими допущениями: интенсивность потребления является известной и постоянной величиной; время поставки заказа является известной и постоянной величиной; каждый заказ поставляется в виде одной партии; затраты на осуществление заказа не зависят от размера заказа; затраты на хранение запаса пропорциональны его размеру. В системе управления запасами с течением времени уровни запасов уменьшаются, пополнение запасов происходит за счет поступления заказа. Затем процесс повторяется [8–10].
Рассмотрим случай, когда заказ для пополнения запасов является одной партией. В таком случае количество запасов убывает с постоянной интенсивностью, пока не достигает нуля. Затем поступает заказ, размер которого равен Q, и уровень запасов восстанавливается до максимального значения. Таким образом, допускается, что спрос известен заранее и что пополнение запасов происходит мгновенно. Теперь определяем наиболее экономичный размер заказа, который обеспечивает работу нашей модели при минимальных издержках. Каждый производственный период связан с затратами на подготовительно-заключительные операции. Будем считать, что затраты на подготовительно-заключительные операции не зависят от того, какое количество продукции будет закуплено, поэтому годовые затраты на подготовительно-заключительные операции пропорциональны числу производственных периодов за год.
Определение наилучшего размера партии можно сформулировать в виде математической задачи [11–13]. Пусть S – годовой сбыт, N – число производственных периодов в году Co – затраты на подготовительно-заключительные операции, Cu – издержки хранения запасов, приходящиеся на единицу запасов (стоимость материалов, рабочей силы и других постоянных расходов), k – годовая процентная ставка, налагающаяся на капитал. Для начала будем считать, что общие переменные издержки Е включают в себя только две составляющие Cu и Co.
Годовые издержки хранения запасов определяются по формуле
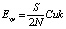, (1)
где S/2N – среднее число единиц хранящегося товара.
Общие годовые затраты на подготовительно-заключительные операции составляют
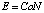. (2)
Сумма этих двух величин равна общим годовым переменным издержкам
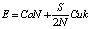. (3)
Оптимальным числом производственных периодов является No, минимизирующее (3). Чтобы найти No, найдем производную по N и приравняем ее к нулю:
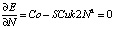, (4)
откуда
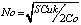(5)
является минимумом, так как вторая производная положительна.
Количество продукции, заказанной за один период Qo (или размер заказа), при котором издержки минимальны, равняется общему годовому спросу, деленному на число производственных периодов, обеспечивающих работу при минимальных издержках:
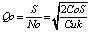. (6)
Теперь найдем размер заказа Q. Учитывая, что q = S/N, где q – размер заказа, формулу (3) можно записать в виде
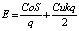. (7)
Дифференцируя по q, получаем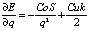 
. Отсюда находим решение нашей задачи (формула Уилсона) в виде
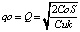. (8)
Выражения (5) и (6) можно записать в другой форме [14]. В некоторых отраслях удобно говорить о запасах, имея в виду их стоимости, выражая годовое потребление через стоимость проданных товаров. Годовое потребление можно записать как A = SCu. Размер заказа определяется по формуле q = QCu. Теперь можно записать выражения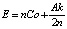 
и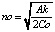 
. Стоимость заказа составляет
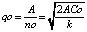. (9)
Стоимость среднего размера запасов составляет qo/2. Средний размер запасов, выраженный через годовой сбыт, равен
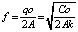. (10)
Логарифмируя, получаем
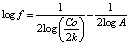. (11)
Первый член правой части этого выражения – постоянная величина, так как Co и k – постоянные. Разовые поставки дорогостоящих товаров должны быть невелики.
2.2. Модель управления запасами при постоянной интенсивности спроса, нулевом времени доставки заказа и издержках вследствие дефицита
Рассмотрим случай, когда имеется дефицит и издержки вследствие дефицита. Полностью проанализировать влияние дефицита на различные политики управления запасами можно, только когда каждому дефициту будут сопоставлены определенные издержки. Вместо нахождения издержек вследствие дефицита можно исследовать политику управления запасами и вычислить величину этих издержек при такой политике [15–17]. Значение издержек вследствие дефицита для политики управления запасами проиллюстрируем на примере.
Рассмотрим задачу управления запасами, в которой дефицит будет наблюдаться во время t1 и задолженный спрос удовлетворяется при поступлении заказа Q'. Будем полагать, что спрос равномерный и что допускается возможность дефицита. Будем использовать следующие обозначения: Co – издержки выполнения заказа или затраты на подготовительно-заключительные операции; Cu – издержки хранения, приходящиеся на единицу товара; Cz – издержки вследствие дефицита, приходящиеся на единицу товара в течение единицы времени, k – процентная ставка на капитал, вложенный в запас, Q' – размер заказа, S – годовой спрос, N = S/Q – число заказов, подаваемых за год, t – длительность цикла заказа, tN = 1 год, M – максимальный запас. В данном случае в каждом цикле наличные запасы имеются в течение промежутка t1 и средний размер этих запасов равен M/2. Дефицит наблюдается в течение промежутка t2, и среднее число недостающих единиц товара составляет (Q' – M)/2. По определению t = t1 + t2. По геометрическому построению получаем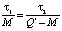 
, следовательно, 
, 
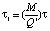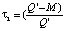. Общие переменные издержки за период t будут состоять из трех частей: издержки выполнения заказа, издержки хранения запасов и издержки вследствие дефицита.
Следовательно, будем иметь следующие общие издержки:
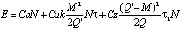. (12)
Так как
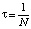, (13)
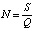, (14)
то, следовательно,
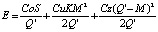. (15)
Дифференцируя данное уравнение по M и Q' и приравнивая результаты к нулю, получаем оптимальные значения M и Q':
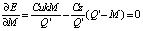. (16)
Следовательно,
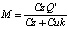. (17)
3. Компромиссное решение в динамической модели многоагентного взаимодействия
Рассмотрим динамическую модель многоагентного взаимодействия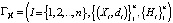 
функционирования предприятия, где I – множество акционеров, 
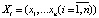– множество политик управления, a 
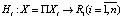, функция выигрыша i игрока, причем у каждого акционера имеется своя собственная функция издержек хранения запасов 
.
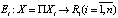Функция дохода акционера i выражается формулой
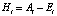, (18)
где Ai – общий доход акционера i.
У каждого акционера свои издержки Ei, состоящие из Cui (стоимость продукции) и Coi (затраты на подготовительно-заключительные операции), Noi (оптимальное число производственных периодов), Xi – множество политик управления.
Годовые издержки хранения запасов определяются по формуле
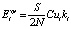, (19)
где S/2N – среднее число единиц хранящегося товара.
Общие годовые затраты на подготовительно-заключительные операции составляют
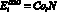. (20)
Сумма этих двух величин равна общим годовым переменным издержкам
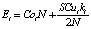. (21)
Трудность заключается в том, что подобранные коэффициенты Cui, Coi дают различное оптимальное число периодов.
Пусть теперь Cui, Coi – издержки двух типов, для каждого агента. Решая задачу на оптимизацию для каждого агента, получим разные числа периодов, оптимальных для каждого агента. Таким образом, возникает задача нахождения подходящей политики управления производственным комплексом. В качестве принципа оптимальности принимается компромиссное решение в динамической модели многоагентного взаимодействия.
Пусть X – компактное метрическое пространство.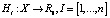 
суть непрерывные функции, Mi = 
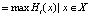. Компромиссное решение CH определяется следующим образом 
.
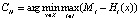Обозначим через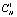 
множество CH. Упорядочим в точке x по величине отклонение от максимума все функции Hi , ... , Hn и выберем те точки 
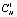, для которых отклонение от максимума второй по порядку функции минимально, и обозначим это множество 
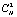. Выразим это следующим образом: 
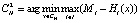. По аналогии определим 
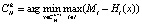для всех k = 1,..., n множества 
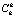компактны [18, 19]. Компромиссным решением 
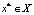называется 
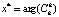, при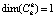 
.
4. Практическая реализация модели Уилсона управления запасами
Рассмотрим простой пример нахождения компромиссного решения. Пусть есть три заинтересованных лица (n = 3): владелец склада, транспортная компания (обеспечивает доставку на склад) и владелец магазина (хранит свои товары на складе). В нашей задаче компромиссным решением будет количество закупок в году. Владелец склада имеет доход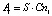 
, где Cn1 – стоимость хранения единицы товара, S – годовой сбыт. Тогда прибыль составит H1 = A1 – E1, E1 – общие издержки, рассчитываемые по формуле (21).
Рассмотрим задачу для конкретного случая. Возьмем стоимость хранения единицы товара Cu1 = 100, годовой сбыт S = 12 единиц товара, годовая процентная ставка k1 = 0,05, затраты на подготовительно-заключительные операции Co1 = 20, прибыль склада будет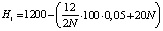 
. Транспортная компания доставляет единицы груза по стоимости Cu2 = 100, S2 = 12, k2 = 0,2, Co2 = 20. Доход будет равен A2 = Cu2∙S2, 
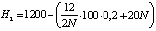. Владелец магазина продает свою продукцию по цене Cu3 = 2000, тогда издержки магазина будут равны E3 = E + A1 + A2. Пусть стоимость единицы товара на оптовом складе равна 1000, тогда H3 = 24000-2400-E3.
Построим модель по доходам в зависимости от количества периодов закупок:
.
Выбирая наибольшее число из каждой строчки, получаем идеальный вектор M = (1150, 1100, 12000). Поскольку первый столбец этого ряда имеет наименьшее значение, то компромиссным решением будет х* = 1.
Заключение
В данной работе рассмотрены математические модели оптимального управления запасами производственного комплекса, которые позволяют минимизировать суммарные издержки хранения запасов. Авторами представлен пример практической реализации построенной динамической модели компромиссного многоагентного взаимодействия. В качестве принципа оптимальности принимается компромиссное решение управления запасами производственного комплекса при многоагентном взаимодействии акционеров. Разработанные авторами статьи математические модели позволяют разработать новые теоретические подходы к исследованию систем управления запасами, пригодных для практического применения.