Актуальность темы исследования определяется тем, что в современных условиях значительной изменчивости финансовых рынков и высокого уровня неопределенности реализации инвестиционных проектов возрастает необходимость в развитии методов оценки и управления стоимостью инвестиционных проектов.
Цель и задачи исследования
Основной целью исследования является повышение эффективности использования ресурсов, привлекаемых для реализации инвестиционных программ промышленных предприятий. Для этого необходимо решить задачи, связанные с иерархической формализацией критериев оценки проекта, формализацией целевой функции и ограничений для решения задачи оптимизации, численным решением задачи оптимизации на базе современных программных продуктов.
Ограниченность ресурсов обуславливает необходимость в решении задачи оптимизации их распределения при реализации конкретных видов работ. При этом можно выделить следующие ограничения, которые принимались во внимание:
- задан объём инвестиций для реализации проекта (критерий – максимум возможного экономического эффекта);
- ограничено количество работников с 32 до 15 чел. (критерий – максимальный эффект от каждого участника проекта при минимальных затратах).
Критерии инвестиционного проекта
В ходе исследования формализованы количественные и качественные критерии с помощью причинно-следственной диаграммы [1], отражающей результат со всеми возможными причинами, влияющими в конечном итоге на эффективную реализацию проекта (рисунок).
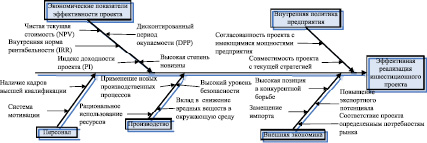
Причинно-следственная диаграмма
Таблица 1
Сводная информация значений синтеза критериев по проектам
|
Обозначение проекта |
Консолидированный критерий оценки проекта (первый уровень) |
|||
|
К1 |
К2 |
К3 |
К4 |
|
|
ИП1 |
0,18 |
0,20 |
0,34 |
0,23 |
|
ИП2 |
0,67 |
0,61 |
0,12 |
0,52 |
|
ИП3 |
0,07 |
0,11 |
0,25 |
0,11 |
|
Значимость базовых критериев |
0,47 |
0,42 |
0,07 |
0,10 |
Оценка эффективности инвестиционного проекта
На основе комплексной оценки инвестиционных проектов для промышленных предприятий целлюлозно-бумажной отрасли проанализированы численные значения критериев и проранжированы следующие проекты [2]:
1) «Энергомодуль на местных топливах» (ИП1) – утилизация отходов предприятий ЦБП на основе современной экологически безопасной плазмо-электрохимической технологии с целью получения электрической и тепловой энергии;
2) «Система энергетического менеджмента» (ИП2) – оптимизация процессов генерации, распределения и потребления топливно-энергетических ресурсов предприятия [3];
3) «Производство древесного угля» (ИП3) – создание дополнительного постоянного источника доходов и диверсификация бизнеса (табл. 1).
Исходя из табл. 1 произведена оценка глобальных приоритетов ИП:
S1 = 0,18·0,47 + 0,20·0,42 + 0,34·0,07 + + 0,23·0,10 = 0,216;
S2 = 0,67·0,47 + 0,61·0,42 + 0,12·0,07 + + 0,52·0,10 = 0,632;
S3 = 0,07·0,47 + 0,11·0,42 + 0,25·0,07 + + 0,11·0,10 = 0,108.
Согласно рассмотренной методике оценки ИП промышленных предприятий все альтернативы были ранжированы в порядке убывания значений показателя глобального приоритета (Si) [4], то есть {ИП2, ИП1, ИП3}. Таким образом, наиболее значимым явился проект «Система энергетического менеджмента».
Решение задачи оптимизации
Согласно полученным ранее результатам ранжирования проектов для оптимизации выбран проект «Организация и внедрение системы энергетического менеджмента (СЭнМ)», обладающий хорошей экономической эффективностью. В табл. 2 показана структура стадий проекта, представляющая собой перечень этапов и работ, каждому этапу соответствуют ориентировочная длительность и стоимость. По перечисленным параметрам поэтапно рассчитывается количество рабочих часов, работников и человеко-часов, а также тарифная ставка, определяющая размер оплаты труда всех работников за час. Тарифная ставка, количество работников и человеко-часов были получены на основе опыта и знаний аналогичных проектов.
Таблица 2
Сроки и стоимость выполнения работ проекта
|
Наименование этапа |
Стоимость выполнения работ, млн руб. |
Срок реализации, мес. (ч.) |
Тарифная ставка, руб./ч |
Количество работников, чел. |
Количество человеко-часов |
|
Разработка и согласование ТЗ |
0,2 |
2 (330) |
606,06 |
2 |
660 |
|
Проведение диагностического аудита |
0,6 |
3 (494) |
1214,57 |
6 |
2964 |
|
Разработка СЭнМ |
1,6 |
8(1317) |
1214,88 |
10 |
13170 |
|
Внедрение СЭнМ |
1,2 |
6 (988) |
1214,57 |
13 |
12844 |
Таблица 3
Результаты решения задачи оптимизации
|
Переменные данной задачи |
Предполагаемые значения |
Численное решение задачи оптимизации с помощью программных пакетов |
|
|
Scilab |
EasyNP |
||
|
Количество человеко-часов на разработку и согласование ТЗ (x1) |
660 |
600 |
641 |
|
Количество работников (x2) |
2 |
2 |
3 |
|
Количество человеко-часов на проведение диагностического аудита (x3) |
2964 |
2900 |
2900 |
|
Количество работников (x4) |
6 |
8 |
8 |
|
Количество человеко-часов на разработку СЭнМ (x5) |
13170 |
13000 |
13000 |
|
Количество работников (x6) |
10 |
10 |
10 |
|
Количество человеко-часов на внедрение СЭнМ (x7) |
12844 |
12000 |
12000 |
|
Количество работников (x8) |
13 |
12 |
12 |
|
Стоимость выполнения работ (млн руб.) |
3,6 |
3,41 |
3,36 |
Каждый этап состоит из перечня работ. С помощью диаграммы Ганта можно представить график работ по проекту.
Ниже представлены основные формулы (1) и (2), участвующие в формализации целевой функции и ограничений.
Ч = Х·Т, (1)
где Ч – количество человеко-часов; Х – количество работников; Т – время, потраченное на выполнение работы.
Ц = ЗП / РЧ, (2)
где Ц – стоимость человеко-часа; ЗП – заработная плата всех работников за этап; РЧ – количество рабочих часов каждого этапа проекта.
Целью оптимизации является сокращение затрат на реализацию этапов инвестиционного проекта, которая обуславливает необходимость уменьшения численных значений параметров (количество человеко-часов и работников на каждом этапе). Обозначим: F(x) – инвестиции в проект; x1, x3, x5, x7 – количество человеко-часов; x2, x4, x6, x8 – количество работников.
Решим задачу нелинейной оптимизации [5], для чего определим минимальное значение целевой функции.
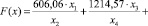
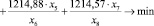 (3)
(3)
при следующих условиях-ограничениях, сформированных при помощи формул (1) и (2):
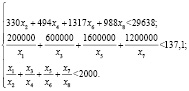 (4)
(4)
Таблица 4
Параметры задачи оптимизации
|
Параметры данной задачи |
Полученные параметры задачи оптимизации с помощью программных пакетов |
|
|
Scilab |
EasyNP |
|
|
Количество итераций |
40 |
619 |
|
Погрешность измерения |
0,001 |
0,001 |
|
Время выполнения (с) |
0,275 |
0,4 |
Кроме указанных ограничений (4) были введены нижние и верхние границы переменных, например количество всех работников, участвующих в проекте, должно быть от 15 до 32 и количество человеко-часов не должно превышать 29638.
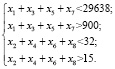 (5)
(5)
На основании сроков и стоимости выполнения работ проекта (табл. 2) были определены минимальные и максимальные величины переменных с помощью формулы (1)
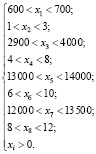 (6)
(6)
Для решения задачи нелинейного программирования были использованы программные пакеты Slilab и Easy NP. Slilab-система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений [6]. Easy NP – приложение для создания математической модели, то есть описания задачи в виде множества переменных и ограничений, а также генетического поиска оптимального решения.
В табл. 3 приведены результаты решения задачи нелинейной оптимизации на базе рассматриваемых программных продуктов. Видно, что количество человеко-часов уменьшилось на каждом этапе и стоимость выполнения получилось минимизировать в той и другой программе. Однако наилучшее решение получилось с помощью программного приложения Easy NP, поскольку показатель стоимости выполнения работ уменьшился на 0,24 млн руб. против уменьшения в 0,19 млн руб., полученного в системе нелинейного программирования Scilab.
В Easy NP, исходя из особенностей модели, устанавливаются параметры генетического поиска и математических вычислений [7]. Поиск решений в Scilab осуществляется за 40 итераций, а в Easy NP– за 619. При этом известно, что чем меньше итераций, тем более эффективным является процесс. Однако это не означает, что решение, найденное с помощью генетического алгоритма, не оптимально (табл. 4). Погрешность измерения в той и другой программе устанавливается равной 0,001, тем самым обеспечивается высокая точность вычислений.
В рассматриваемом случае метод генетического алгоритма подходит больше, поскольку имеет ряд преимуществ: не имеет значительных математических требований к видам целевых функций и ограничений, алгоритм позволяет эффективно отыскать глобальный оптимум, то есть значение целевой функции (3).
Заключение
Представлена процедура оптимизации различных ресурсов (стоимость выполнения работ, количество работников, количество человеко-часов), участвующих в реализации инвестиционного проекта «Организация и внедрение системы энергетического менеджмента (СЭнМ)», с использованием пакетов прикладных математических программ, позволяющих учесть уровень сэкономленных инвестиций. По результатам решения задачи оптимизации можно сделать вывод об эффективности использования генетического алгоритма в программе Easy NP, который предлагает наиболее выгодный вариант распределения инвестиций, но согласно полученным параметрам (количество итераций, быстродействие выполнения) превосходит Scilab. Выбор наилучшего варианта реализации задачи оптимизации подразумевает в первую очередь результат целевой функции, программа Easy NP справилась с этим лучше. Многокритериальная оценка предоставляет возможность проводить выбор лучшего инвестиционного проекта и рационально использовать финансовые ресурсы в условиях их ограниченности.



