Разрабатываемая математическая модель предназначена для изучения теплового состояния кристаллизующейся заготовки прямоугольного сечения в горизонтальной машине полунепрерывного литья заготовок (ГМПЛЗ), в качестве которого используется сплав 960 пробы серебра [1, 7].
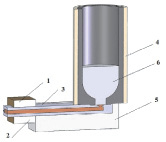
Рассмотрим кристаллизатор ГМПЛЗ для отливки прямоугольного сечения [2, 8]. Особенностью его конструкции является наличие нижней и верхней частей для графитового кристаллизатора и медного охлаждающего устройства (рис. 1). Основные геометрические размеры графитового кристаллизатора показаны на рис. 2, а медного охладителя – на рис. 3 [3]. Для получения отливки прямоугольного сечения 200×20 мм используется графитовый кристаллизатор и медный охладитель.
 а
а 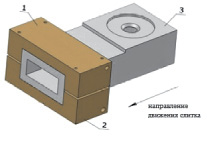 б
б
Рис. 1. Общий вид ГМПЛЗ для получения заготовок прямоугольного сечения (а) и графитовый кристаллизатор с медным охладителем (б): 1 – верхняя часть охлаждающего устройства; 2 – нижняя часть охлаждающего устройства; 3 – верхняя часть графитового кристаллизатора; 4 – тигель; 5 – теплоизолятор; 6 – расплав
Рис. 2. Основные размеры ГМПЛЗ
Известно, что в жидкой фазе (жидком ядре слитка) тепло переносится не только теплопроводностью, но и конвекцией, например по данным работ по изучению теплового состояния слитка в кристаллизаторах МНЛЗ [4–6]. Причинами этого являются естественная конвекция перегретого расплава, перемешивание расплава струей подаваемого жидкого металла, электромагнитные и другие воздействия на жидкое ядро слитка. Движение расплава в незатвердевшей части слитка существенно усложняет расчет затвердевания слитка, поскольку для корректного учета явлений тепло- и массопереноса в жидкой фазе необходимо, наряду с уравнением теплопроводности, принимать во внимание систему уравнений движения жидкости и неразрывности [4].
Упрощение задачи достигается при введении эффективного коэффициента теплопроводности жидкой фазы λэф, значение которого увеличено по сравнению с коэффициентом молекулярной теплопроводности λж в определенное число раз:
λэф = εкλж,
где εк – коэффициент конвекции, зависящий от интенсивности движения расплава. Ввиду низкой начальной скорости струи металла в ГМПЛЗ принимаем εк = 1–2 [4]. Таким образом, эффективная теплопроводность жидкой фазы может превышать теплопроводность неподвижной фазы. Возрастание эффективной теплопроводности в жидком металле при его перемешивании приводит к увеличению теплоотдачи на фронте фазового перехода, разогреву твердой фазы и соответственному увеличению теплоотдачи на поверхности слитка.
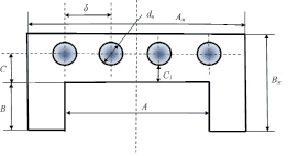
Рис. 3. Основные размеры медного охлаждающего устройства
При работе в установившемся режиме рассматриваемый графитовый кристаллизатор ГМПЛЗ в разных точках имеет температуру от 100 до 600 °С. Для этого диапазона температур для теплопроводности λ^ получено уравнение линейной регрессии:
λ(t) = 127,28 – 0,11657t, Вт/(м К),
где λ^ – коэффициент теплопроводности для графита в направлении перпендикулярном прессованию.
С его использованием среднеинтегральное значение теплопроводности в этом диапазоне температур составляет
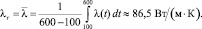
Известно, что серебро и его сплавы можно отливать при температуре всего лишь на 50 градусов выше температуры ликвидуса. Скорость разливки или скорость вытяжки в общем случае зависит от ширины заготовки, температуры расплава на входе в кристаллизатор и свойств металла. Основным фактором, определяющим скорость разливки, является толщина твердой корки на выходе из кристаллизатора. Скорость воды в каналах в общем случае зависит от ширины a, толщины b заготовки и скорости разливки v (таблица).
Основные допущения и ограничения математической модели
Задачу затвердевания заготовки решаем в декартовой системе координат. За начало отсчета принимаем середину нижней стороны прямоугольника вертикального сечения внутреннего канала кристаллизатора, проходящего через ось тигля. Расположение осей координат и направление движения слитка  показано на рис. 4. Видно, что в общем случае областью моделирования тепловых процессов является параллелепипед ABCDA′B′C′D′.
показано на рис. 4. Видно, что в общем случае областью моделирования тепловых процессов является параллелепипед ABCDA′B′C′D′.
При разработке математической модели теплового состояния слитка были приняты следующие допущения и ограничения:
1. Принимаем, что температура в данной точке слитка в стационарном режиме разливки не зависит от времени (в системе отсчета, связанной с Землей), то есть рассматриваем квазистационарный тепловой режим.
2. Считаем, что температура существенно меняется вдоль осей x и z. Дело в том, что толщина слитка b существенно меньше его ширины a, конструкция кристаллизатора и охладителя такова, что охлаждение более интенсивное со стороны граней BB′C′C и AA′D′D (рис. 3 и 4). Граничные условия на боковой грани ABCD такие же, как на A′B′C′D′, то есть наблюдается симметрия температурных полей относительно плоскости EFGH, в которой dT/dy = 0. Для достижения поставленных задач моделирования с целью упрощения принимается dT/dy << dT/dx. Рабочей областью моделирования теплового состояния слитка является прямоугольник EFGH.
3. Для затвердевания жидкого металла используется квазиравновесная модель, при этом считается, что в двухфазной зоне отсутствует диффузионное переохлаждение.
4. В зоне охлаждения медным охладителем на его границе с графитовым кристаллизатором принимаем среднее значение коэффициента теплоотдачи, зависящего от конструкции охладителя и параметров охлаждающей воды.
Основные технологические параметры процесса вытяжки слитка из ГМПЛЗ
|
№ п/п |
Наименование величины |
Обозначение |
Единица измерения |
Величина |
|
1 |
Перегрев расплава на выходе из плавильного тигля над точкой ликвидус |
ΔT0 |
°С |
50100 |
|
2 |
Температура расплава на выходе из плавильного тигля |
T0 = Tl +ΔT0 |
°С |
9201020 |
|
3 |
Скорость разливки |
v |
см/мин |
1020 |
|
4 |
Температура охлаждающей воды |
tв |
°С |
25 |
|
5 |
Скорость воды в каналах |
Wв |
м/c |
14 |
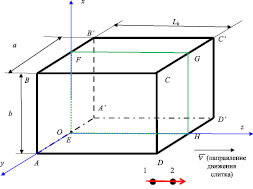
Рис. 4. Область моделирования теплового состояния слитка и выбранная декартовая система координат
5. Считаем, что в направлении оси Oz тепло передается только конвекцией. Покажем это. Определяющим для соотношения роли конвекции и теплопроводности является число Пекле:
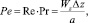
где Δz – характерный размер вдоль движения, где наблюдается градиент температур dT/dz, это расстояние можно оценить как Lk ≈330 мм = 0,33 м; Wz = v – скорость разливки.
Минимальная скорость разливки Wz = v = 10 см/мин = 16,6•10–4 м/с, коэффициент температуропроводности для твердой фазы вблизи Ts равен a = 1,22•10–4 м2/c. При этих условиях Pe ≈ 5. Известно, что при Pe > 1 можно пренебречь распространением тепла за счет теплопроводности. Это означает, что если выбрать любые две точки 1 и 2, имеющие одинаковые координаты x, y и разные координаты z (z2 > z1), то температура второй точки зависит от температуры первой, а температура первой не зависит от второй при выбранном направлении движения слитка (рис. 4).
Математическая модель теплового состояния слитка
В основе математической модели теплового состояния слитка лежит нелинейное уравнение теплопроводности, которое дополняется начальными и граничными условиями; при этом учет теплоты затвердевания производится с помощью квазиравновесной теории двухфазной зоны.
Согласно первому и второму допущениям распределение температуры в затвердевающем слитке в системе отсчета, связанной с Землей, описывается стационарным уравнением энергии с учетом внутреннего источника тепла:
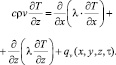 (1)
(1)
Выделим в двухфазной зоне слитка контрольный объем V0 и введем в рассмотрение относительное количество твердой фазы 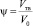 – отношение объема, занимаемого твердой фазой, к полному объему выделенного элемента двухфазной зоны (доля твердой фазы). Параметр Ψ для жидкой фазы равен нулю
– отношение объема, занимаемого твердой фазой, к полному объему выделенного элемента двухфазной зоны (доля твердой фазы). Параметр Ψ для жидкой фазы равен нулю 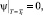 для полностью затвердевшей части слитка равен единице
для полностью затвердевшей части слитка равен единице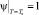 и для двухфазной зоны изменяется от нуля до единицы, Ts, Tl – температура солидуса и ликвидуса материала заготовки соответственно [4].
и для двухфазной зоны изменяется от нуля до единицы, Ts, Tl – температура солидуса и ликвидуса материала заготовки соответственно [4].
Будем полагать, что функция источника тепла qv(x, y, z, τ) прямо пропорциональна локальной скорости затвердевания расплава 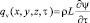 , причем удельная теплота плавления L играет роль коэффициента пропорциональности.
, причем удельная теплота плавления L играет роль коэффициента пропорциональности.
Рассмотрим тепловое состояние тела в системе координат, связанной с произвольным сечением заготовки, движущимся вместе со слитком. Учитывая соотношение 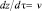 , получим
, получим
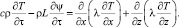 (2)
(2)
Скорость затвердевания расплава 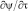 в уравнении (2) в общем случае определяется закономерностями роста кристаллов в переохлажденном расплаве. Однако в настоящее время закономерности зарождения и роста кристаллов для большинства металлов и сплавов изучены недостаточно полно. В связи с этим скорость затвердевания расплава определяется на основе гипотезы о квазиравновесном протекании процесса затвердевания [4]. Согласно этой гипотезе, если кристаллизация сплава идет довольно медленно, то есть полностью протекают процессы диффузионного обмена примесью между жидкой и твердой фазами, а также внутри самих фаз, то соблюдается равновесный процесс кристаллизации сплава и относительное количество твердой фазы, находящейся в равновесии с жидкостью при температуре T, может быть определено из диаграммы состояния сплава по правилу рычага.
в уравнении (2) в общем случае определяется закономерностями роста кристаллов в переохлажденном расплаве. Однако в настоящее время закономерности зарождения и роста кристаллов для большинства металлов и сплавов изучены недостаточно полно. В связи с этим скорость затвердевания расплава определяется на основе гипотезы о квазиравновесном протекании процесса затвердевания [4]. Согласно этой гипотезе, если кристаллизация сплава идет довольно медленно, то есть полностью протекают процессы диффузионного обмена примесью между жидкой и твердой фазами, а также внутри самих фаз, то соблюдается равновесный процесс кристаллизации сплава и относительное количество твердой фазы, находящейся в равновесии с жидкостью при температуре T, может быть определено из диаграммы состояния сплава по правилу рычага.
В наиболее простом случае сечение твердой фазы Ψ определяется кусочно-непрерывной функцией, график которой представлен на рис. 5.
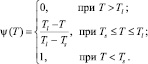 (3)
(3)
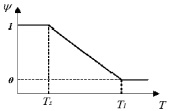
Рис. 5. Вид функции относительного содержания твердой фазы Ψ(T)
В этом случае темп кристаллизации сплава внутри интервала от Tl до Ts является постоянной величиной, равной
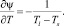 (4)
(4)
С учетом допущения о возможности пренебречь распространением тепла за счет теплопроводности в направлении Oz и используя подстановку
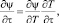
уравнение (2) можно записать как
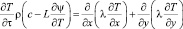
или более подробно
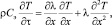 (5)
(5)
где 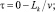 Cэ, λ, ρ – эффективная теплоемкость, теплопроводность и плотность материала затвердевающего слитка.
Cэ, λ, ρ – эффективная теплоемкость, теплопроводность и плотность материала затвердевающего слитка.
Эффективная теплоемкость, теплопроводность и плотность материала затвердевающего слитка представляются кусочно-непрерывными функциями [5]:
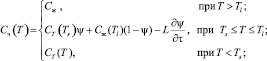 (6)
(6)
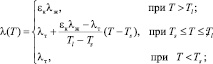 (7)
(7)
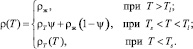 (8)
(8)
Для решения краевой задачи уравнение (5) необходимо дополнить начальным и граничными условиями.
Начальное условие определяет температурное поле расплава в начальный момент времени на выходе из плавильного тигля (при τ = 0, 0 < x < b)
T(x, 0) = T0 = TL + ΔT0. (9)
На сторонах FG и EH слитка (рис. 4), находящихся в контакте с рабочей стенкой кристаллизатора, задаются следующие граничные условия.
Для определения граничного условия при теплоотдаче от затвердевающей жидкости использовался метод конечных объемов. Для элемента объема, имеющего форму параллелепипеда f Δx, лежащего вблизи поверхности охлаждающей стенки площадью f, должно выполняться условие теплового баланса. Количество отводимого тепла кристаллизатором q при температуре металла выше Ts равно количеству тепла фазового перехода, описываемого эффективной теплоемкостью элемента объема 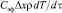 , и количеству тепла, переданного из объема расплава
, и количеству тепла, переданного из объема расплава 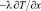 .
.
Исходя из этого граничные условия:
для x = b, z = τ•v
при T > Ts,
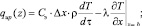
при T ≤ Ts,
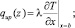 (10)
(10)
для x = 0, z = τ•v
при T > Ts,
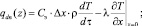
при T ≤ Ts,
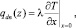 (11)
(11)
где qup(z), qdn(z) – тепловые потоки в кристаллизатор с верхней и нижней поверхностей слитка.
Таким образом, полученные уравнения (5)–(11) составляют математическую модель теплового состояния слитка в ГМПЛЗ.
В результате проведенной работы развита математическая модель, описывающая тепловое состояние и процесс кристаллизации заготовки из драгоценного сплава, отливаемого на ГМПЛЗ небольшой производительности и позволяющая определить для затвердевающей заготовки, как изменяется по времени температурное поле слитка при различных технологических режимах работы ГМПЛЗ.



