Расчет собственных частот и форм изгибных колебаний бруса батана широких металлоткацких станков
При проектировании широких станков возникает задача определения оптимального числа лопастей и зоны их расположения по длине бруса батана. Данная задача иначе, как методами динамики решена быть не может [2, 5]. Остановимся на модели с n лопастями (рис. 1). Как частные случаи эта модель позволяет проанализировать:
– двухлопастной вариант с расположением лопастей в концевых сечениях бруса (m2 = 0, c2 = 0);
– двухлопастной вариант со смещенным относительно концевых сечений бруса расположением лопастей (m1 = 0, c1 = 0);
– трехлопастной вариант с двумя ведущими лопастями (l2 = 0, m2 = m1/2, c2 = 0);
– трехлопастной вариант с тремя ведущими лопастями (l2 = 0, m2 = m1/2, c2 = c1/2);
– четырехлопастной вариант с двумя ведущими лопастями (c1 = 0).
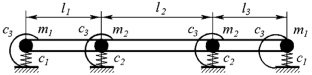
Рис. 1. Динамическая модель изгибных колебаний бруса батана для широких металлоткацких станков
Участки бруса в общем случае могут иметь разную жесткость EJ и распределенную массу m. По технической теории каждый из участков будет иметь свое уравнение собственных колебаний [1, 6]
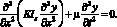(1)
Решение этого уравнения имеет вид
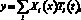(2)
где Xi(x) – функция формы; Ti(t) – функция времени.
Имея в виду, что момент инерции бруса относительно нейтральной оси Iz = const, получим уравнение форм
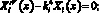
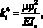(3)
где ρi – собственные частоты изгибных колебаний. Колебания при этом носят гармонический характер, поскольку функция времени определяется уравнением
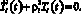(4)
Решение уравнения форм в общем виде представим как
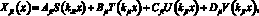(5)
где j – номер рассматриваемого участка (j = 1, 2, 3, ..., n – 1); i – номер собственной формы (частоты) колебаний; A, B, С, D – постоянные коэффициенты;
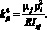
Граничные условия и условия сопряжения для данной модели будут иметь вид
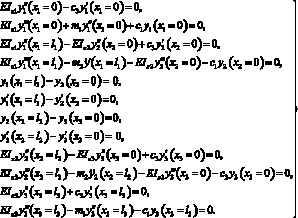(6)
Подставляя в эту систему решение (2) с учетом (4) и (5) будем иметь, опуская индексы i,
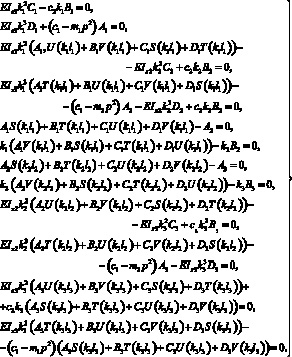(7)
Частотное уравнение принимает вид
(8)
где а(k, l) – коэффициенты при неизвестных Aj, Bj, Cj, Dj[ в системе уравнений (7).
Для определения форм колебаний положим в системе (7) А1 = 1, тогда, не принимая во внимание, например, последнее уравнение этой системы, будем иметь
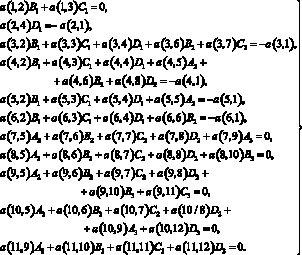(9)
Система (9) позволяет найти коэффициенты Aji, Bji, Cji, Dji (j = 1, 2, 3, …, n; A1i = 1), определяющие формы собственных колебаний бруса.
Как отмечалось ранее, упругое сопротивление knydx со стороны опушки вырабатываемой сетки, действующее во второй фазе движения батана, не изменяет форм собственных колебаний бруса, меняются только собственные частоты, которые будут равны
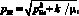
где рIi – собственные частоты колебаний системы на первой фазе движения, определяемые уравнением (8).
Не оказывает влияние на формы упругих колебаний системы и неупругое сопротивление. Собственные частоты при этом будут равны
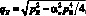
для первой фазы движения батана и
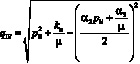
для второй фазы движения батана.
Во второй фазе движения батана собственные формы колебаний бруса, если следовать технической теории [6], не меняются.
Расчет собственных частот и форм крутильных колебаний бруса батана широких металлоткацких станков
При анализе крутильных колебаний динамическая модель бруса батанного механизма с n лопастями может быть представлена в виде сплошного n-опорного вала (рис. 2).
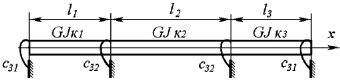
Рис. 2. Динамическая модель крутильных колебаний бруса батана для широких ткацких станков
Опоры упругие. Коэффициенты жесткости этих опор – приведенные к крутильным коэффициенты изгибной жесткости лопастей и подбатанного вала с учетом радиальной жесткости его подшипниковых опор. Для каждого j-го участка бруса, с учетом уравнения Эйлера – Пуассона [3, 4], уравнение чисто крутильных собственных колебаний бруса равно
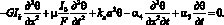(10)
Используя метод Фурье, решение уравнения (10) ищется в форме
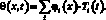(11)
Общее решение (11), равное сумме частных, приобретает вид
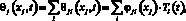j = 1, 2, 3, (12)
где функция формы
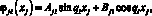0 ≤ xj ≤ lj. (13)
Частоты собственных колебаний бруса
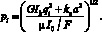(14)
Граничные условия и условия сопряжения для рассматриваемой модели имеют вид
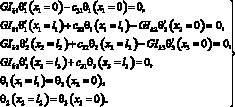(15)
Подставляя в условия (15) частное решение, получим
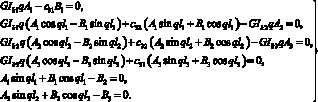(16)
Обозначим коэффициенты при неизвестных Aj, Bj:
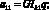
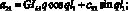
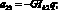
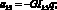
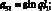
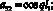
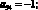
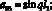
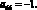
Неизвестные параметры qi функции формы (13) определяются из уравнения
(17)
Для определения форм крутильных колебаний бруса положим в уравнениях (16) A1i = 1. Тогда
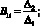
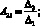
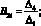
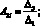
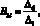
где
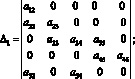
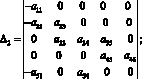
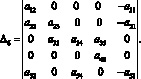
Выводы
Разработаны динамическая и математическая модели собственных частот и форм изгибных и крутильных колебаний бруса батана широких металлоткацких станков с n лопастями, соответствующие его уточненной динамической модели на фазе взаимодействия берда с опушкой вырабатываемой сетки.