В настоящее время исследователями всё больше внимания уделяется проблемам обеспечения надёжности зданий и сооружений. Надёжность сооружений, прежде всего, зависит от надёжности их конструктивных элементов, это перемычки, стропильные фермы, стеновые панели, колонны. Большое значение играет выбор математических моделей, адекватно описывающих напряженно-деформированное состояние таких конструкций. Основу таких моделей составляют диаграммы деформирования композита и волокна, которые являются интегральной характеристикой физико-механических свойств материалов и могут быть описаны различными математическими выражениями, что предопределяет точность получаемых расчётных данных. В качестве основных математических моделей, описывающих механику разрушения изгибаемых конструкций из композитов, армированных непрерывными волокнами (арматура), целесообразно использовать нормативную модель согласно современным нормам проектирования и модели расчета на основе реальных диаграмм деформирования материалов.
а б
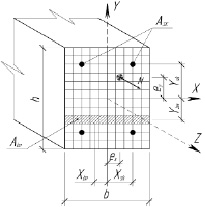
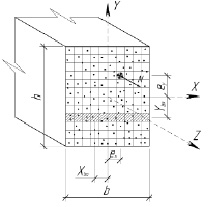
Схема поперечного сечения изгибаемого неоднородного элемента:а – с непрерывными волокнами; б – с дискретными волокнами
Анализ математических моделей по оценке напряженно-деформированного состояния анизотропных сред на примере железобетонных конструкций показал, что более точно отразить фактическое состояние композитных элементов под нагрузкой позволяет нелинейно-деформационная модель, предложенная В.Н. Байковым, Н.И. Карпенко, Б.С. Расторгуевым [1, 2, 5]. Данная модель основывается на условиях равновесия нормального сечения, разбитого на дискретные участки матрицы композита и непрерывного стального волокна (рис. 1, а). Учет физической нелинейности работы конструкций производится с помощью математического описания диаграмм деформирования каждого композита и применения шагово-итерационного метода, реализующего способ упругих решений А.А. Ильюшина. Суть метода заключается в том, что решение нелинейной задачи получается в виде последовательности решений линейных задач, сходящихся к результату. Условия равновесия внешних и внутренних сил при любом загружении записываются в виде
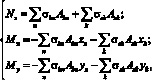 (1)
(1)
где Nz – продольная сила; Mx – изгибающий момент в направлении оси X; My – изгибающий момент в направлении оси Y.
Выбранный для исследования способ описания диаграмм деформирования материалов является наиболее оптимальным, поскольку он позволяет вычислять напряжения в матрице и в стальном волокне (арматуре) по единообразным зависимостям на каждом этапе кратковременного нагружения:
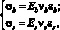 (2)
(2)
где σb, σs – соответственно напряжения в матрице и волокне; Eb, Es – модули упругости материалов; εb, εs – относительные деформации.
По результатам многочисленных опытов к настоящему времени как в нашей стране, так и за рубежом разработано большое количество различных способов описания диаграмм деформирования матрицы и стального стержня (непрерывного волокна), выдвинуто множество предложений по их построению [4, 7]. В работах В.В. Адищева, В.Н. Байкова, Н.И. Карпенко и др. [2] предложены аналитические зависимости для описания диаграмм деформирования материалов σ = f(ε). На основании выполненных теоретических и экспериментальных исследований был сделан вывод, что наиболее удовлетворительно производится аппроксимация реальных диаграмм деформирования с помощью сплайн-функций или по способу переменных секущих модулей.
При аналитическом описании таких диаграмм используется коэффициент изменения секущего модуля, определяемый из условия
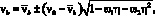 (3)
(3)
где 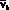 – значение коэффициента изменения секущего модуля матрицы νb (0 < νb < 1) в вершине диаграммы (
– значение коэффициента изменения секущего модуля матрицы νb (0 < νb < 1) в вершине диаграммы (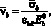
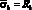 – прочность матрицы; εbr – относительная деформация при максимальном напряжении;
– прочность матрицы; εbr – относительная деформация при максимальном напряжении; 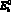 – начальное значение модуля упругости матрицы); η – уровень напряжений (
– начальное значение модуля упругости матрицы); η – уровень напряжений (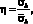 ,
,
0 < η < 1); ν0 – значение коэффициента в начале диаграммы (ν0 = 1 при построении восходящей ветви диаграммы и 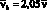 при построении нисходящей); ω1, ω2 – параметры кривизны диаграммы, определяемые по формулам:
при построении нисходящей); ω1, ω2 – параметры кривизны диаграммы, определяемые по формулам:
– для восходящей ветви:
– для нисходящей ветви:
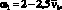 ω2 = 1 – ω1;
ω2 = 1 – ω1;
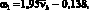 ω2 = 1 – ω1. (4)
ω2 = 1 – ω1. (4)
Секущий модуль упругости матрицы при любом значении напряжения определяется по формуле
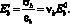 (5)
(5)
В ряде случаев удобно использовать зависимости, предложенные в европейских нормативных документах (EКБ-ФИП):
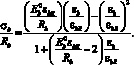 (6)
(6)
Данные аналитические выражения применимы для описания с высокой достоверностью диаграмм растяжения и сжатия низкопрочностных композитов, в частности мелкозернистых матриц.
После выполнения соответствующих преобразований система (1) приводится к виду
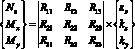 (7)
(7)
или
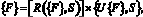 (8)
(8)
где {F} = {Nz, Mx, My}т – вектор-столбец внешних сил, принимаемый в зависимости от схемы загружения; [R({F}, S)] – матрица жесткости для нормального сечения, являющаяся функцией {F} и S, элементы которой корректируются на каждом этапе загружения; {U{F}, S} = {ez, kx, ky}Т – вектор-столбец деформаций, получаемый в результате решения системы уравнений (8).
Затем, исходя из гипотезы плоского деформирования, вычисляются деформации в матрице и стальном волокне для каждого дискретного участка:
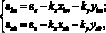 (9)
(9)
где ez – деформации элемента на уровне продольной оси Z; kx, ky – соответственно значения кривизны в направлении осей X и Y; xbn, ybn – координаты центра тяжести дискретных элементов матрицы; xsk, ysk – координаты центра тяжести дискретных элементов непрерывных стальных волокон.
Деформационная модель для расчета прочности включает:
– уравнения равновесия внешних и внутренних сил в нормальном сечении:
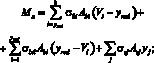 (10)
(10)
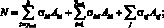 (11)
(11)
– уравнения, устанавливающие распределение деформации в матрице и непрерывном волокне по нормальному сечению, исходя из условия плоского поворота и плоского смещения сечения (гипотезы плоских сечений):
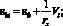
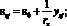 (12)
(12)
– уравнения, определяющие связь между напряжениями и относительными деформациями матрицы и непрерывного волокна в композите
σbi = f(εbi); σsj = f(εsj). (13)
В уравнениях (10)–(13): Мx, N – изгибающий момент и продольная сила от внешней нагрузки; Abi, Vi, σbi и εbi – площадь, расстояние от нижней растянутой грани элемента до центра тяжести i-го элементарного слоя матрицы композита, напряжение и деформация на уровне его центра тяжести; Asj, ysj, σsj и εsj – площадь, координаты центра тяжести j-го непрерывного волокна, напряжение и деформация в нем; ε0 – относительная деформация волокна, расположенного на пересечении выбранных осей X и Y; 1/rx – кривизна в плоскости действия момента Mx.
Для изгибаемых в плоскости симметрии поперечного сечения элементов система уравнений для расчета прочности по деформационной модели имеет вид
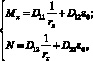 (14)
(14)
где Dij (i, j = 1, 2) – жесткостные характеристики, определяемые по формулам
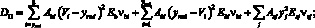 (15)
(15)
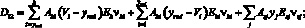 (16)
(16)
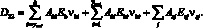 (17)
(17)
Коэффициенты упругости i-го участка матрицы νbi, νbti и j-го непрерывного волокна νsj определяются по формулам
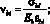
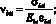
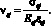 (18)
(18)
Напряжение и относительные деформации сжатой и растянутой матрицы композита и стального непрерывного волокна σbi, εbi, σbti, εbti, σsj, εsj определяют из приведенных выше зависимостей для диаграмм состояния матрицы и стального волокна (3)–(6).
Для определения напряжений и относительных деформаций сжатого и растянутого элемента композиционного материала, армированного дискретными волокнами (рис. 1, б), σfbi, εfbi, σfbti, εfbti необходимо проведение дополнительных исследований и соответствующих экспериментов для получения математических зависимостей σfbi = f(εfbi) и σfbti = f(εfbti), описывающих работу композиционного материала как в упругой стадии, так и в стадии трещинообразования.
Выводом таких зависимостей занималось множество исследователей. Кокс полагал, что тонкое дискретное волокно длиной l заключено в упругой матрице, а соединение волокна с матрицей является идеальным. При создании напряжений в волокне, действующих в осевом направлении, деформации на границах раздела матрицы и волокна являются одинаковыми. Торцы волокон в такой модели не передают напряжений. Другую модель предложил Аутуотер. Он показал, что окружающая дискретное волокно матрица при затвердении сжимается, что приводит к появлению на поверхности раздела матрицы и волокна сжимающих напряжений. При действии нагрузки в направлении волокна на поверхности раздела возникают силы трения, которые обусловливают появление в волокне напряжения σf. Если использовать коэффициент трения μ и предел текучести матрицы σmy, то можно определить σf. Модель Кокса впоследствии была модифицирована Дау и Розеном.
Перечисленные модели обладают общими недостатками: они описывают поведение композитов, армированных дискретными волокнами, которые ориентированы перпендикулярно плоскости нормального сечения элемента. Более того, данные модели становятся неприменимы при описании работы композитов, армированных волокнами сложной геометрии, отличной от прямой и цилиндрической, – стальные фибры с единичными и множественными отгибами по обоим концам, волнистые фибры. Поведение таких композитов описывается более сложными уравнениями. Последние экспериментальные и теоретические исследования [8, 6] позволили на основе кусочно-линейных характеристических кривых получить более приемлемые зависимости, определяющие значения σfbt:
– при εfbt = 0: σfbt = 0;
– при

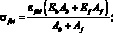
– при
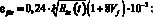
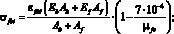
– при
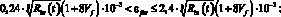
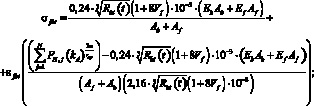
– при
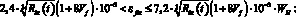
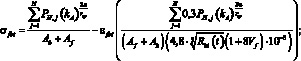
– при
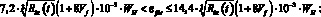
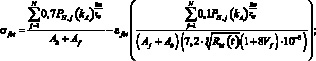
– при
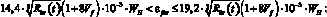
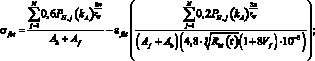
– при
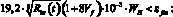
σfbt = 0.
Здесь
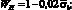
 (19)
(19)
WH, PH – соответственно абсцисса и ордината первой характеристической точки кусочно-линейной диаграммы «нагрузка-смещение», описывающей работу дискретного волокна при смещении из матрицы [6]; lf,an – длина заделки дискретного волокна (мм); N – количество дискретных волокон в композите; n – количество дискретных волокон, расположенных в радиусе 10 мм и влияющих на работу единичного центрального волокна; rср – среднее расстояние до фибр, расположенных в радиусе 10 мм; kA – коэффициент, учитывающий работу центральной фибры в результате влияния на неё соседних фибр [3].



