Знание весовых коэффициентов, умение их правильно находить и оперировать ими при моделировании в значительной степени определяет правильный выбор системы критериев качества композиционных материалов (КМ). При этом значение правильного выбора весовых коэффициентов возрастает, когда рассматривается большое количество конкурирующих систем качества КМ со многими параметрами. Поэтому весовые коэффициенты для частных показателей должны определяться не субъективно (хотя и с определенной достоверностью), а с математическим обоснованием. В каждом конкретном случае необходимо четко представлять, для какого класса КМ определяются весовые коэффициенты, так как математическая модель, построенная для одного класса КМ, будет иной для другого [1, 2, 6, 9].
Если параметры, определяющие эффективность, являются функцией времени, то и значения весовых коэффициентов также являются функцией времени. Например, стоимость и надежность материала изменяют в зависимости от времени изготовления. В начале выпуска продукции её стоимость велика, а надежность мала. По мере увеличения выпуска продукции и отработки технологии стоимость уменьшается, а надежность растет.
Для определения весовых коэффициентов кроме построения математической модели КМ необходимо также получить информацию о возможных значениях параметров и частных показателей качества конкурирующих вариантов компонентов КМ.
Пусть задана модель эффективности композита, описываемая функцией от частных показателей качества E = F(y1, y2, ..., yn),
причем все частные показатели являются независимыми переменными. Влияние частного показателя качества на главный показатель определим, взяв полный дифференциал функции:
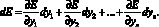(1)
Частные производные представляют весовые коэффициенты частных показателей качества y1, у2, ..., уn, связанных функциональной зависимостью с главным показателем Е, так как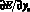 
показывает (при фиксированных значениях остальных показателей), как изменяется Е при изменении yi, т.е. 
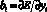. Уравнение (1) запи-
шем в виде
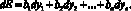(2)
Из (1) и (2) следует, что коэффициенты веса bi, определенные из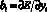 
, являются функциями многих переменных частных показателей качества уi, поскольку последние при определении bi принимались вполне определенными, т.е. bi = f(y1, y2, ..., yn) [4].
Если рассматривается модель КМ, для которой заданы значения уi , то bi можно получить подстановкой конкретных значений частных показателей качества. Для упрощения решения задачи определения эффективности КМ полагаем, что весовые коэффициенты не связаны между собой и не зависят от значений самих частных показателей качества.
Таким образом, чтобы приступить к определению bi, надо построить математическую модель эффективности как функцию частных показателей качества и стоимости в виде E = F(y1, y2, ..., yn, C).
Общий алгоритм её построения зададим следующими этапами [2]:
1) на основании анализа исследуемого класса КМ разрабатываем математическую модель работы системы в функции ее параметров и частных показателей качества;
2) составляем математическую модель стоимостных характеристик композита с учетом проектирования, внедрения, модернизации и эксплуатации;
3) производим выбор показателя эффективности, отражающего назначение композита;
4) анализируем характер частных показателей качества;
5) на основе результатов п. 1–4 формируем математическую модель эффективности композита.
Характер частных показателей качества определяет вид полученной модели эффективности. Она может быть детерминированной или статистической. Это существенно влияет на дальнейшее определение их числовых значений.
Если частные показатели качества являются детерминированными величинами, то по уравнениям E = F(y1, y2, ... yn, C)
и bi = f(y1, y2, ..., yn, C) можно рассчитать детерминированные числовые значения эффективности и весовых коэффициентов, на чем и заканчивается определение эффективности для данного КМ.
В том случае, когда частные показатели качества являются случайными величинами, модель эффективности представляется как статистическая модель. Весовые коэффициенты в этом случае являются случайными величинами, так как случайны сами значения частных показателей качества. Для получения bi в виде постоянных значений находят математическое ожидание М(bi) и дисперсию D(bi). Последняя характеризует разброс значений данного весового коэффициента, а следовательно, и разброс значений коэффициента эффективности системы:
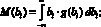
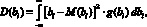(3)
где g(bi) – закон распределения величины bi.
Классификация методов определения весовых коэффициентов частных показателей качества КМ, используемых при математико-статистических исследованиях, представлена на рисунке. В каждом конкретном случае выбор метода определяется характером имеющейся информации о частных показателях качества КМ [1, 2, 3, 7].
Определение экономической эффективности КМ связано со значительными трудностями, особенно на стадии проектирования или изготовления, так как к этому времени имеется мало данных для моделирования.
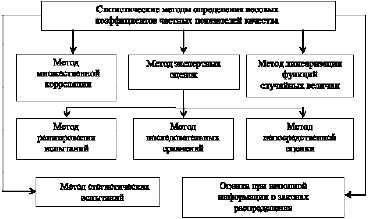
Классификация статистических методов определения весовых коэффициентов
частных показателей качества
Однако, имея даже неточные исходные данные, можно прийти к правильным выводам, если известны пределы и направления изменения стоимости и последствия ошибок, возникшие в результате допущенных неточностей. При выборе вариантов на стадии моделирования вариантов речь идет о сравнительном анализе технико-экономической эффективности. В этом случае представляет интерес не сама стоимость, а относительная составляющая разности стоимости вариантов [5, 10, 8].
Основу при определении экономической эффективности составляет расчет стоимости КМ. Рассмотрим некоторые методы расчета стоимости КМ на стадии разработки и моделирования. Их рассмотрение необходимо для сравнительной оценки и выбора наилучшего метода учета стоимости при моделировании и многокритериальном синтезе эффективных композитов специального назначе-
ния [5, 10, 8].
Метод удельных весов основан на определении себестоимости КМ по удельному весу отдельных составляющих в общей себестоимости. При этом используются следующие принципы
сопоставимости:
- технологические (назначение, удобоукладываемость, одинаковость технологических процессов изготовле-
ния и т.п.);
- эксплуатационные (плотность, прочность, морозостойкость и т.п.).
Себестоимость проектируемого материала определяется на основе данных о структуре и себестоимости аналогичных материалов:
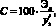(4)
где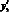 
– удельный вес (в процентах) определенного элемента затрат в себестоимости аналогичного материала; Эл – сумма затрат на данный элемент во вновь проектируемом материале.
Этот метод целесообразно использовать для случаев, когда вновь проектируемый материал изготавливается на том же предприятии, что и аналог.
Метод аналогий близок к методу удельных весов. Стоимость подсчитывается как произведение C = aсСа, где Са – стоимость материала-аналога; aс – коэффициент сопоставимости, который в зависимости от сложности аналога имеет пределы 0,5 ≤ aс ≤ 1,5. Аналогично, метод используется для случаев, когда вновь проектируемый материал улучшает свойства аналога.
Графоаналитический метод используется тогда, когда нет данных по материалу-аналогу. Реализация его требует предварительного исследования по группе КМ, к которой может быть отнесен моделируемый КМ. Он основан на построении математической модели стоимостной характеристики Сз = f(См + Cк) – зависимости основной заработной платы от стоимости материалов и технологической оснастки. Эта зависимость может быть представлена в виде
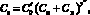(5)
где С0, у″ – коэффициенты, определяемые в результате предварительных исследований различных групп КМ.
Тогда заводская себестоимость
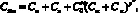(6)
где
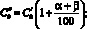(7)
a – процент цеховых расходов; b – процент общезаводских расходов.
Метод основан на том, что стоимость материалов и технологической оснастки на стадии проектирования уже может быть ориентировочно определена. Метод применим на стадии производства КМ и совершенно неприменим при стадии поисковых научных исследований.
Метод сметной калькуляции является наиболее точным, однако он применим только на стадии освоения опытной партии, когда вопрос о выборе рецептурно-технологических параметров КМ уже решен. Применять этот метод на стадии моделирования невозможно, так как нет достоверных данных о норме расхода основных материалов, не известна трудоемкость изготовления КМ по видам работ.
Определение стоимости систем по средней стоимости основных компонентов КМ основано на построении подробной иконографической модели рецептурно-технологических параметров КМ в виде блок-схемы и оценки стоимости отдельных блоков и элементов, количество которых ограничено.
Разбив систему на классы по элементам и определив стоимость элементов Сi i-го класса, находим стоимость системы суммированием
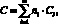(8)
где ni и m чаще всего известны или могут быть определены уже на стадии предварительного проектирования. Стоимость Сi определяется по стоимости блоков системы, выпускаемых промышленностью композиционных материалов.
Этот метод наиболее прост в применении, так как при известных Cicp надо знать только количество элементов, в то время как остальные методы требуют подробного расчета одной из составляющих основных материальных трудовых затрат, что не всегда возможно сделать. При использовании достоверных данных средних стоимостей компонентов КМ погрешность метода не превышает 10 % [2, 4, 5].
Именно метод определения стоимости систем по средней стоимости основных компонентов КМ использовался для оценки экономической эффективности разрабатываемых композитов.
Разработанный математический метод формирования весовых коэффициентов критерия практической оптимальности в дальнейшем использовался в процессе компьютерно-имитационного моделирования структуры и свойств композиционных материалов при формировании критерия оптимальности и функции качества композитов на минеральной и полимерной основах для защиты от агрессивных факторов.
Статья публикуется при поддержке гранта № 3018 базовой части Госзадания вузам на 2016 год.