Согласно Базель II операционный риск (ОР) представляет собой риск убытка в результате неадекватных или ошибочных внутренних процессов, действий сотрудников и систем или внешних событий. Данное определение включает юридический риск, но исключает стратегический и репутационный риски. Это определение имеет универсальный характер, так как оно применимо для всего многообразия финансовых институтов. Кроме того, в определении сразу выделяются и источники операционного риска.
Согласно Базель II, для расчета величины операционного риска следует использовать один из трех подходов:
1. Подход базового индикатора (BIA – Basic Indicator Approach).
2. Стандартизированный подход (SA – Standartized Approach).
3. Усовершенствованный (продвинутый) подход (Advanced Measurement Approach).
Согласно масштабному исследованию LDCE (Loss Data Collection Excersice), проведенному Базельским комитетом, результаты которого были опубликованы в 2009 году, во всех мировых регионах величина отчисляемого на покрытие ОР при расчете посредством BIA и SA капитала превосходит капитал, отчисляемый после расчетов по методам AMA [2]. Одно из требований Базель II к банку для использования АМА состоит в том, что разработанная им система оценки уровня ОР обязана использовать четыре элемента: внутренние данные об операционных потерях, внешние данные об операционных потерях, анализ сценариев, а также факторы бизнес-окружения и внутреннего контроля банка.
Внешние данные в чистом виде непригодны для использования при калибровке модели, выстраиваемой банком, так как они не отражают подверженность банка операционному риску. Для того чтобы внешние данные дополняли внутренние данные банка и не вредили качеству модели, перед использованием их необходимо масштабировать. В данной статье предлагается решение задачи масштабирования внешних данных о потерях от ОР.
Масштабирование частоты и величины потерь от ОР
В подходе LDA моделируются два значения – частота и величина потерь. Следовательно, для правильного использования внешних данных надо масштабировать оба значения. Кроме того, так как в рассмотрении находится продолжительный период, то необходимо произвести корректировку данных с учетом временной стоимости денег. В том случае, если внутренние и внешние данные представлены в разной валюте, необходимо привести их к одной.
Значение величин потерь при масштабировании внешних данных должно быть определенным образом скорректировано на основе заранее выбранных параметров, показывающих различие двух финансовых институтов. Это, к примеру, может быть валовый доход, как показатель величины банка, масштаба его деятельности – подразумевается, что чем крупнее бизнес, тем больше он подвержен операционному риску [8].
В случае масштабирования частоты потерь результатом процедуры должно стать возможное сокращение выборки внешних данных в том случае, если данные от какого-либо банка описывают либо слишком редкие, либо слишком частые (по сравнению с исследуемым банком) случаи потерь за взятый период.
В литературе встречаются различные подходы к задаче масштабирования внешних данных потерь от операционного риска [1, 4, 8]. Для вывода строгой математической формы, допустим, что каждая потеря имеет вид [7]:
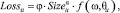
где φ – некий постоянный компонент всех потерь; α – показатель масштабирования размера банка; f (ω, θit) – функция специфичных для потери аргументов θit; в которых содержится информация о бизнес-линии и природе рискового события, вектор ω содержит коэффициенты параметров риска; Size – переменная, которая может характеризовать размер банка, в котором произошла потеря. Это может быть, к примеру, валовый доход, размер активов или количество сотрудников, а также функция этих параметров. В литературе для представления размера банка часто используется степенная функция [8].
Предположим, что аргументы функции f содержат все количественные факторы рискового события, тогда логарифм f можно представить в следующем виде:
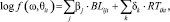
где BLijt – параметр j-й бизнес-линии и RTikt – параметр k-го типа риска, оба имеющие отношение к рисковому событию i, произошедшему в момент времени t. Тогда логарифм величины потери можно записать в следующем виде:
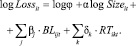
Это представление может быть использовано для поиска нужных коэффициентов α и ω. Масштабирование внешних данных о рисковом событии, которое произошло в банке А, отвечает на вопрос, какой величины была бы эта потеря, если бы то же самое событие произошло в банке В. Для составления уравнения можно использовать факт наличия в обоих событиях постоянного компонента j:
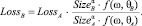
Оценив масштабирующие коэффициенты, при помощи данной модели можно определить эквивалентную величину любой внешней потери для конкретного банка, используя любой набор переменных, характеризующих рассматриваемые банки [4].
Еще один аспект, необходимый к рассмотрению, состоит в том, все ли внешние данные есть смысл использовать, учитывая разницу рисковых профилей различных банков. К примеру, если калибровать модель, выстраиваемую российским банком, внешними данными о банках США, то логично предположить, что результаты моделирования будут не такими, как в случае, если бы использовались данные только от банков конкретного региона. Однако повсеместно отмечаемая нехватка данных об экстремальных потерях заставляет извлекать максимум информации буквально из каждого единичного случая.
В качестве модели для формирования выборки можно использовать модель Хекмана [6]. Для каждой записи из набора внешних данных, необходимо решить, включать ее в калибровочную выборку или не включать. Величина банка здесь рассматривается как фактор неоднозначного влияния – очевидно, что размер банка может оказывать негативное влияние на события операционного риска (произойдет оно или не произойдет), и в том случае, если оно происходит, величина потери будет также обусловлена размерами банка. Первая составляющая модели определяет дихотомическую переменную z, которая показывает, наблюдается ли операционная потеря в рассматриваемый период среди всего множества банков, данные о потерях которых имеются:
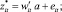
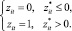
Вторая часть модели определяет размер потери:
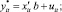
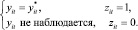
Переменная z – это реализация латентной переменной z* с нормально распределенными независимыми ошибками e, которые имеют нулевое математическое ожидание и дисперсию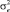 
. Потеря заданной величины наблюдается только в том случае, когда z принимает значение 1. Переменная y – это наблюдаемая реализация другой латентной переменной y* c с нормально распределенными независимыми ошибками u, которые имеют нулевое математическое ожидание и дисперсию 
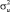. Если коэффициент корреляции между e и u равен нулю, то метод наименьших квадратов (МНК) дает несмещенные оценки. Модель Хекмана позволяет использовать внешнюю информацию от банков, которые не испытывали экстремальных потерь, что улучшит оценку неизвестных параметров.
Есть несколько параметров банка, которые можно рекомендовать для включения в эту модель. Например, это могут быть:
- Средняя величина заработной платы сотрудников. Этот параметр в целом отражает распределение разных типов сотрудников внутри банка, а также их уровень образованности и профессионализма. Зарплаты коррелируют с качеством менеджмента, и предполагается, что чем выше этот показатель, тем меньше у банка шансов испытать потерю экстремальной величины.
- Капитализация банка. К примеру, этот показатель может рассчитываться как отношение собственных средств банка к размеру активов. Предполагается, что более «капитализированные» в этом смысле банки будут более подвержены операционному риску, так как они будут чувствовать себя «более защищенными» за счет большого объема собственных средств.
- Макроэкономический показатель. В этом качестве может выступать ежегодный прирост ВВП. Как отмечается в литературе, во время спадов экономического роста операционные потери становятся более частыми. С другой стороны, высказывается мнение, что в такие периоды активность банков снижается и вместе с этим уменьшается размер операционных потерь [3].
На вопрос о том, какие параметры следует или не следует включать в регрессионную модель, может ответить статистический тест, например тест Вальда. В частности, в работе [4] при работе с некоторой выборкой оказалось, что включение в регрессию показателя капитализации банка не является значимым.
Второй параметр, который необходимо масштабировать, – это частота потерь. Если потери в банке происходят часто, то внешние данные о слишком редких потерях могут «испортить» выборку, и наоборот. Масштабируя внешние данные под конкретный банк, необходимо ответить на вопрос, какова была бы частота этих событий, если бы они происходили в данном банке. Впервые модель масштабирования частоты наступления операционных убытков была предложена в работе [4].
Число событий ОР, произошедшее в банке за фиксированный период, зависит от различных факторов, описывающих характеристики этого финансового института. Логично предположить, что большое значение имеет размер банка – чем больше банк, тем больше он совершает транзакций, имеет больше сотрудников, больше активов, а следовательно, и более подвержен событиям операционного риска. Стоит учитывать также и макроэкономические показатели, поскольку во время спадов в экономике банковская активность снижается, численность персонала уменьшается, что потенциально может снизить качество управления. Таким образом, данные факторы целесообразно использовать для масштабирования частоты потерь методами регрессионного анализа.
Частота наступления событий обычно моделируется при помощи вероятностных распределений дискретного типа, поэтому целесообразно использовать распределение Пуассона или отрицательное биномиальное распределение. Эти распределения имеют гибкие параметры, которые, в свою очередь, зависят от значений, определяющих характеристики финансового института, в котором произошло то или иное событие ОР. Таким образом, когда будут вычислены параметры регрессии, станет возможным и вычисление моментов распределения (математическое ожидание, дисперсия) для данного банка. Подробнее вопрос о выборе распределений частоты убытков будет рассмотрен далее.
Поскольку операционные потери, особенно значительные, в некоторых однородных группах случаются сравнительно редко, множество внешних данных потенциально содержит много нулевых значений, как за отдельно взятый период, так и за весь период наблюдений. Такая ситуация также может возникнуть, когда во внимании находятся только большие операционные потери, например, при установлении большого порога отсечения. Для моделирования подобных ситуаций целесообразно использовать так называемые «модели с концентрированными нулями» (zero-inflated models).
Рассмотрим модель, основанную на предположении, что частота операционных событий подчиняется закону Пуассона. Пусть Yi – число потерь, которые претерпел банк i за период наблюдения – распределено по закону Пуассона, параметр распределения λi примем равным Xib. Дисперсия равна математическому ожиданию и равна λi. Так как в выборке потенциально присутствует большое количество нулевых значений, то целесообразно оценить вероятность числа условных потерь, учитывая этот факт. Модель с учетом концентрированных нулевых значений может выглядеть следующим образом:
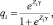
где Zi – это вектор независимых переменных, параметры g оцениваются одновременно с b по методу максимального правдоподобия. Расчет λi и qi для конкретного банка проводится с использованием полученных оценок коэффициентов независимых переменных. В модели Пуассона с концентрированными нулями дисперсия и математическое ожидание больше не равны и соотносятся следующим образом:
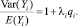
Смысл перехода от модели Пуассона к модели на основе негативного биномиального распределения состоит в отражении факта, что предыдущая модель может учитывать не все внешние факторы, которые заключены в векторе экзогенных переменных Xi. В данной модели принимается
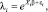
где εi – «ошибка», которая показывает влияние на зависимую переменную, неучтенное за счет выбора независимых переменных и независящее от них. В данном случае λi является случайной переменной, в отличие от модели Пуассона.
Если предположить, что εi имеет некую функцию плотности распределения, а величина µi = exp(εi) имеет гамма-распределение и при этом E(µi) = 1, а Var(µi) = α, то получается, что Yi имеет отрицательное биномиальное распределение [5]. После расширения модели для данных с концентрированными нулями выводятся следующие параметры:
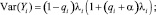
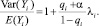
Если все предположения выполнены, то оценку параметров γ, β и α можно вычислить по методу максимального правдоподобия. Для каждого конкретного банка далее можно вычислить λi и qi.
Таким образом, если, к примеру, использовать в качестве внешних факторов величину активов банка (Assetsi), показатель капитализации (Bank capi), средний размер заработной платы (Mean sali) и рост ВВП (GDPi), то параметры распределений примут следующий вид (где r и pi – параметры негативного биномиального распределения):
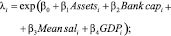
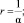
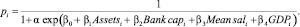
Заключение
С помощью имеющегося математического аппарата можно обоснованно совмещать данные об операционных потерях из внутренних и внешних источников при помощи масштабирования. Однако большинство моделей являются достаточно требовательными к объему выборки, и это имеет особую важность для оценки операционного риска, когда речь идет о потенциальном присутствии крайне редких событий экстремальной величины и оценке высоких квантилей за пределами имеющихся в калибровочной выборке значений.
Валидация моделей оценки операционного риска является сложной задачей. Согласно философии Карла Поппера, критерием «научности» теории или модели является ее фальсифицируемость, то есть существование методологической возможности её опровержения путём постановки эксперимента. Таким образом, принимать модели оценки капитала можно в том случае, если есть теоретическая возможность получить данные, наличие которых может привести к отвержению полученных результатов.
В случае с оценкой операционного риска разными исследователями было показано [3], какой ненадежной может быть итоговая оценка с учетом требования Базель II к квантилю. Одним из простых шагов к решению данной проблемы в России может стать консолидация данных о банковских операционных потерях за счет создание консорциумов, с одной стороны, и создание регулятивной базы, направленной на разработку и улучшение стандартов отчетности, с другой стороны, так как на сегодняшний день раскрытию данных в первую очередь препятствует нежелание банков делиться фактами о потерях от реализации риска.