Важной функцией интеллектуальных систем управления можно считать прогнозирование. Для прогнозирования применяется большое число подходов и методов. Представляет интерес логическое прогнозирование. К методам логического прогнозирования обычно относят создание прогнозного сценария, морфологический анализ, метод исторических аналогий, прогнозирование по образцу (эталону) и др. Перспективным подходом при построении методов логического прогнозирования является использование моделирования рассуждений. Методологической базой для исследования методов прогнозирования, основанных на моделировании рассуждений, в частности логическом выводе на знаниях, можно считать работу [4]. В работе рассмотрен вывод предсказания, описываемого покрывающими моделями (Covering Law Models), состоящими в том, чтобы вывести факт, как частный случай закона. При этом используется дедуктивно-номологическая модель (Deductive Nomological Model), основанная на фактах и дедуктивных законах. Теория логического вывода успешно развивается в работах [1, 9]. Большое внимание уделяется не только дедуктивному, но и абдуктивному выводу [2, 3].
Целый ряд важных теоретических и практических результатов получен в Институте проблем управления РАН в рамках решения проблемы управления плохо определенными динамическими ситуациями с использованием формального описания происходящих процессов в виде когнитивных карт [6, 7]. В работе [8] предложен метод логического прогнозирования на основе абдуктивного вывода заключений. Метод благодаря нахождению недостающих в описании ситуации фактов и правил позволяет строить прогнозы в тех случаях, когда на базе дедукции они невозможны. Метод прогнозирует развитие ситуации от заданной начальной до конечной фазы. Однако на практике возникает потребность в прогнозе в условиях, когда известна только одна – начальная фаза. Эта потребность и привела к разработке рассматриваемого далее метода прогнозирования развития ситуации из заданной фазы на основе вывода следствий при не полностью определенной базе знаний.
Для содержательной постановки задачи логического прогнозирования развития ситуаций воспользуемся основными понятиями из работы [8]. Событие в предметной области характеризуется множеством простейших утверждений – фактов, зафиксированных в определенный момент времени. Наступление события происходит в тех случаях, когда определенные подмножества этих фактов становятся истинными. В простейшем случае событие может представляться одним фактом. Ситуация в предметной области характеризуется совокупностью событий и отношений между ними. Ситуация складывается тогда, когда наступают характеризующие её события и устанавливаются необходимые отношения между ними. В простейшем случае ситуация может представляться одним событием. Фаза развития (состояние) ситуации представляется подмножеством событий и отношений, описывающих ситуацию. Ситуация входит в некоторую фазу, как только наступают характеризующие её события и устанавливаются необходимые отношения между ними. Траектория развития ситуации – последовательность фаз, через которые проходит развитие ситуации. Предсказание траектории развития ситуации – определение для ситуации, находящейся в текущей фазе (состоянии), одной или нескольких фаз (состояний), в которые перейдет ситуация в последующие моменты времени. Введённые понятия позволяют сформулировать основную задачу прогнозирования развития ситуаций как задачу предсказания траектории (траекторий) развития ситуации.
Формальное описание задачи прогнозирования как задачи логического вывода следствий
Формальное описание задачи P логического прогнозирования развития ситуации из заданной фазы может быть определено следующим образом:
P = <mC, mS, mP, r>,
где mC – множество новых событий; mS – множество текущих событий и ситуаций с отношениями между ними; mP – множество прогнозируемых фаз (состояний) развития ситуации; r – множество результатов прогнозирования, которое может содержать схему логического прогнозирования S, а также прогнозируемые в следующий момент времени фазы (состояния) m1 и последовательности фаз (состояний) mL. Для упрощения описания задачи прогнозирования как задачи логического вывода введем ряд определений.
Определение 1. Задача дедуктивного вывода следствий формулируется следующим образом: при заданном множестве исходных посылок MP для некоторого (нового) набора фактов MF определить множество следствий MS (утверждений, которые будут следовать из новых фактов при использовании исходных посылок). При этом если вывод успешен, то могут быть определены логические цепочки вывода, объясняющие нити рассуждений.
Определение 2. Задача вывода следствий при не полностью определенной базе знаний формулируется следующим образом: при заданном множестве исходных посылок MP для некоторого (нового) набора фактов MF определить множество следствий MS (утверждений, которые будут следовать из новых фактов при использовании исходных посылок) и множество дополнительных фактов MD, необходимых для успешного вывода следствий и не противоречащих исходным посылкам.
Определение 3. Формула
X1 & X2 &…& XK → Y
называется формулой непосредственного логического следования, символы X1, X2, …, XK, Y – литералами, а символ «>» – знаком логического следования, который разделяет формулу на левую (антецедент) и правую (консеквент) части. Знаки конъюнкции в формуле могут быть опущены.
Определение 4. Выражение X, X → Y ⇒ Y интерпретируется как вывод из факта X с помощью правила X → Y следствия Y.
Определение 5. Схемой логического вывода называется ориентированный граф, вершинам которого сопоставлены формулы (номера формул) посылок, причем, входящие дуги помечены литералами из левых, а исходящие – из правых частей формул, и вершины соединены между собой в соответствии с суперпозицией их формул в выводе; литералы свободных исходящих дуг графа соответствуют конечным следствиям. Следствие считается конечным, если из него не следует ни одно утверждение.
Пример 1. Задачу вывода следствий при не полностью определенной базе знаний можно проиллюстрировать на следующем простейшем примере [9]. Исходные посылки:
1) A;
2) ABX → C;
3) CY → E.
Новый факт:
4) B.
Дедуктивный вывод следствий из факта B завершается неудачно: из факта В с помощью заданных исходных посылок не выводится ни одного следствия.
Вывод следствий при не полностью определенной базе знаний позволяет вычислить дополнительные факты 5) X и 6) Y, благодаря которым из факта В с помощью заданных исходных посылок будут выводиться следствия C и E. Следствие E является конечным, так как из него не следует утверждений. Схема логического вывода для данного примера приведена на рис. 1. Номера вершин в схеме соответствуют номерам формул посылок, а соединение вершин выполнено в соответствии с суперпозицией формул в выводе. Вершина нового факта выделена жирной линией, а вершины дополнительных фактов – пунктиром.
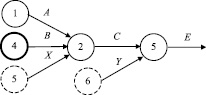
Рис. 1. Схема логического вывода следствий C, E из нового факта B
Таким образом, рассматриваемый вид вывода следствий позволяет продолжить решение задачи вывода следствий из новых фактов в тех случаях, когда с помощью дедуктивного вывода это невозможно.
Формальное описание задачи DA вывода следствий при не полностью определенной базе, соответствующее задаче логического прогнозирования P, можно представить следующим образом: DA = <MF, MP, MD, MS, R>, где MF – множество новых фактов; MP – множество текущих фактов и правил; MD – множество дополнительных фактов, формируемых при успешном выводе; MS – множество следствий; R – множество результатов логического вывода, которое может содержать: схему логического вывода S (используемую в качестве схемы прогнозирования), литералы утверждений (фаз, состояний), непосредственно следующих из фактов текущего шага M1 и последовательности литералов утверждений (фаз, состояний) ML. Формальное описание задачи прогнозирования как задачи вывода следствий при не полностью определенной базе знаний позволяет строить метод прогнозирования, который дает возможность в процессе прогнозирования вычислять недостающие в базе знаний факты.
Метод логического прогнозирования на основе вывода следствий при не полностью определенной базе знаний
Логическое прогнозирование представляет собой циклический процесс, состоящий из ряда шагов. Перед началом этого процесса задача логического прогнозирования формулируется как задача логического вывода следствий при не полностью определенной базе знаний:
DA = <MF(t), MP(t), MD(t), MS,R>,
где MF(t) – множество новых фактов; MP(t) – множество текущих фактов и правил; MD(t) – множество дополнительных фактов, сформированных в процессе логического вывода, MF(t) – множество фактов, поступивших на шаге t. Первоначально t = 1. Предполагается, что объединение множеств MF(1) и MP(1) образует непротиворечивое множество, а MD(1) = Ø. В процессе прогнозирования выполняются следующие действия.
1. Принимается новое множество фактов MF(t). Если последнее конечное следствие совпадает с одним из принятых фактов, то прогнозирование завершается (выполняется пункт 9), иначе при t = 1 выполняется пункт 3, а при t > 1 – следующий пункт.
2. Проверяется успешность прогноза: совпадение состояний, определяемых новым множеством фактов MF(t) и ранее спрогнозированных состояний. Если прогноз успешен, то выполняется пункт 6, иначе следующий пункт.
3. Производится решение задачи дедуктивного вывода следствий MF(t) & MP(t) ⇒. Если логический вывод завершается успешно, то выполняется пункт 5, иначе следующий пункт.
4. В том случае, когда прогнозирование с помощью дедуктивного вывода невозможно, выполняется вывод следствий при не полностью определенной базе знаний [5]. Если этот вывод следствий успешен: сформировано такое множество дополнительных фактов MD(t), которое обеспечивает дедуктивный вывод следствий Ms, и объединенное множество MD(t) ∪ MP(t) ∪ MF(t) непротиворечиво, то выполняется следующий пункт, иначе – пункт 9 (прогнозирование с помощью вывода при не полностью определенной базе знаний невозможно).
5. Строится схема успешного логического вывода S.
6. По схеме S для множества фактов MF(t) определяются прогнозируемые состояния (фазы ситуации) M1(t), которые ожидаются на следующем шаге.
7. По схеме S для множества фактов MF(t) формируются цепочки вывода ML(t) от текущего состояния (состояний) до состояний, соответствующих конечным следствиям, которые представляют собой долгосрочные прогнозы.
8. Осуществляется переход к следующему шагу: значение шага t увеличивается на единицу и производится переход к пункту 1.
9. Конец. Прогнозирование завершается.
Переход в методе к следующему шагу соответствует переходу ситуации в новую фазу. При этом происходит сравнение ранее спрогнозированной фазы и фактически наступившей. В случае их несовпадения прогноз на последующее развитие ситуации корректируется с помощью нового логического вывода.
Пример прогнозирования с использованием исчисления высказываний
Рассмотрим прогнозирование на примере задачи диагностики автомобиля [10, с. 283]. Зададим предметную область следующим набором событий:
1) ТД – Топливо поступает в двигатель;
2) ДНВ – Двигатель не вращается;
3) ФГ – Фары горят;
4) ТБ – Топливо есть в баке;
5) ТК – Топливо поступает в карбюратор;
6) ПСЗ – Проблема в свечах зажигания;
7) ПСТ – Проблема в стартере.
Каждому событию соответствует факт, который принимает значение «ИСТИНА», как только становится известно о наступлении соответствующего ему события.
Отношения, определяемые на множестве событий предметной области, могут быть представлены базой знаний:
8) ТД & ДНВ > ПСЗ;
9) ДНВ & ФГ > ПСТ;
10) ТБ & ТК > ТД.
Начальная фаза F1 ситуации, развитие которой прогнозируется, задана событиями ТБ и ДНВ.
Формальное описание задачи логического вывода, соответствующей задаче прогнозирования, имеет следующий вид:
DA = <MF(t), MP(t), MD(t), MS, R>.
Первоначально t = 1. Множество новых фактов MF(1) = {ТБ, ДНВ}. Исходное множество посылок (MP): (8–10). Множество дополнительных фактов MD(1) = Ø.
В процессе прогнозирования выполняются следующие действия.
Шаг 1. При выполнении первого шага дедуктивный вывод следствий завершается неудачно.
1. Принимается новое множество фактов MF(1) = {ТБ, ДНВ}. Поскольку t = 1, то выполняется пункт 3.
3. Производится решение задачи дедуктивного вывода следствий MF(1) & MP(1) ⇒. Дедуктивный вывод следствий завершается неудачно, поэтому выполняется следующий пункт.
4. Выполняется вывод следствий при не полностью определенной базе знаний. Этот вывод следствий успешен. Формируется множество дополнительных фактов MD(1) = {ТК}, которое обеспечивает успешный дедуктивный вывод следствий. Объединенное множество MD(1) ∪ MP(1) ∪ MF(1) непротиворечиво. Формируется множество следствий MS = {ТД, ПСЗ}, в котором следствие ПСЗ является конечным. Выполняется следующий пункт.
5. Строится схема успешного логического вывода S (рис. 2).
6. По схеме S для множества фактов MF(1) определяются прогнозируемые состояния (фазы ситуации), которые ожидаются на следующем шаге (таблица, строка 1).
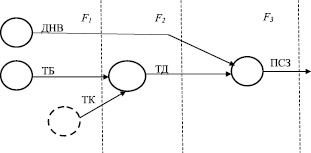
Рис. 2. Схема логического вывода следствий ТД, ПСЗ из новых фактов ДНВ и ТБ
Прогноз и его уточнение по шагам
|
Номер шага, t |
Поступившие факты, MF(t) |
Прогноз на следующий шаг, M1(t) |
Долгосрочный прогноз, ML(t) |
|
1 |
ТБ, ДНВ |
ТК, ТД |
Дедуктивный вывод следствий неудачен. ТБ, ТК, ДНВ ⇒ ТД ⇒ ПСЗ |
|
2 |
ТК, ТД |
ПСЗ |
ТД ⇒ ПСЗ |
|
3 |
ПСЗ |
– |
– |
7. По схеме S для множества фактов MF(1) формируется цепочка вывода от текущего состояния до состояния, соответствующего конечному следствию, которая представляет собой долгосрочный прогноз (таблица, строка 1).
8. Осуществляется переход к следующему шагу: значение шага t увеличивается на единицу и производится переход к пункту 1.
Шаг 2. При выполнении второго шага подтверждается успешность прогноза, сформированного на первом шаге.
1. Принимается новое множество фактов MF(2) = {ТК, ТД}. Поскольку t ≠ 1, то выполняется пункт 2.
2. Проверяется успешность прогноза: совпадение состояний, определяемых новым множеством фактов MF(2) и ранее спрогнозированных состояний. Поскольку прогноз успешен, то выполняется пункт 6.
6. По схеме S для множества фактов MF(2) определяются прогнозируемые состояния (фазы ситуации), которые ожидаются на следующем шаге (таблица, строка 2).
7. По схеме S для множества фактов MF(2) формируется цепочка вывода от текущего состояния до состояния, соответствующего конечному следствию, которая представляет собой долгосрочный прогноз (таблица, строка 2).
8. Осуществляется переход к следующему шагу: значение шага t увеличивается на единицу и производится переход к пункту 1.
Шаг 3. При выполнении третьего шага подтверждается успешность прогноза, сформированного на втором шаге.
1. Принимается новое множество фактов MF(3) = {ПЗС}. Поскольку принятый факт совпадает с единственным конечным следствием, то производится переход к пункту 9.
9. Конец. Прогнозирование завершается.
Прогнозирование осуществляется на основе схемы логического вывода на каждом шаге развития ситуации с учётом поступающих фактов. Прогноз завершается на шаге 3, так как поступивший факт совпадает с единственным конечным следствием. В процессе прогнозируемого развития ситуации выделяются три фазы: F1, F2, F3 (рис. 2).
Заключение
Предложенный метод логического прогнозирования развития ситуаций на основе вывода следствий из новых фактов при не полностью определенной базе знаний позволяет предсказывать траектории развития ситуации из заданной начальной фазы, которая определяется подмножеством фактов. Метод применим, когда прогнозирование на основе дедуктивного вывода следствий невозможно.
Программная реализация метода логического прогнозирования развития ситуаций на основе вывода следствий на знаниях, представленных формулами исчисления высказываний или предикатов, может быть использована при построении интеллектуальных систем прогнозирования. Возможно создание самостоятельных программ логического прогнозирования развития ситуаций. Такие программы, предназначенные для автоматизированной подготовки прогнозной информации для лиц, принимающих решения в условиях постоянно меняющейся обстановки, могут применяться в автоматизированных системах управления различного назначения.
Успешность реализации логического прогнозирования определяется успешностью реализации логического вывода. До недавнего времени главным аргументом против использования методов логического вывода на знаниях, представленных в виде формул исчисления высказываний и предикатов первого порядка, был большой объем вычислений, обусловленный комбинаторным характером задач логического вывода. Однако разработка и применение параллельных методов логического вывода, ориентированных на современные параллельные вычислительные платформы, и технологии параллельного программирования позволяют решать задачи логического вывода за приемлемое время.
Работа выполнена при финансовой поддержке РФФИ (проект № 15-01-02818 а).



