Разработка моделей и алгоритмов принятия обоснованных решений в сложных системах была и остается ключевой проблемой современных научных исследований. Сложная система характеризуется совокупностью элементов и связей, разнообразных по природе и типу, эти элементы и связи динамичны, как следствие, модель сложной системы должна отражать эволюцию ее во времени и пространстве, что усложняет задачу моделирования. Вот почему одним из активно развивающихся сегодня подходов к решению этой проблемы является эволюционное моделирование, описанию отдельных элементов которого и посвящена данная статья, что подтверждает ее актуальность. В [3] подчеркивается, что «в качестве общих свойств сложных динамических систем следует выделить: эволюционность развития, неравновесность, самоорганизацию и самовоспроизведение, нарушение законов симметрии».
Вопрос об «иерархическом порядке» в сложной системе анализируется, обсуждается и раскрывается учеными более 50 лет, и при этом остается немало задач, относительно которых нет четких формализованных ответов. В этой статье мы попытаемся осветить такие задачи в области «иерархического порядка» и эволюционного моделирования, как виды и типы иерархий в сложной системе, подход к формализации задач управления в условиях динамичных видов иерархий, формализация определения обоснованного управления для достижения некоторого эталонного состояния на одном из уровней иерархии.
Организационная структура любой сложной системы многоуровневая, этот постулат не нуждается в доказательстве. В ставшей классикой монографии [6] подробно описана организационная структура многоуровневой системы с точки зрения выделения в ней таких типов иерархий, как:
1) уровень описания, или уровень абстрагирования, называемый стратой;
2) уровень сложности принимаемого решения, называемый – слой;
3) и эшелон как организационный уровень.
Однако в обозначенном труде, как и в большинстве, как правило, рассматривается иерархия в ее классическом понимании (типа «дерево»). И только в последнее время стали появляться работы, в которых рассматриваются динамичные формы иерархий и изучаются свойства систем принятия решений с гетерархической структурой [1], что подтверждает наш выбор.
Теоретический анализ
Современные сложные системы, иерархическое представление, характерные особенности и свойства которых уже анализировались авторами в [10, 11], эволюционируют во времени и пространстве. И в частности, как подчеркивают современные исследователи, например в [5], организационная форма сложной системы обладает свойством гетерархии, что требует формирования новых междисциплинарных методологических подходов. Сравним кратко эти виды иерархий.
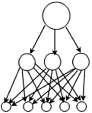
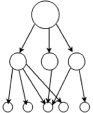
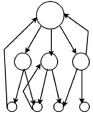
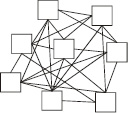
В публикации [7] графически описаны три вида иерархий, рисунок, где холархия – это доминантная иерархия с обратной связью (рисунок, в). Следует отметить, что холархии также бывают полными и неполными. Более прогрессивной и современной формой организационной структуры сложной системы на сегодняшний день является гетерархическая структура. Считается, что в классическом понимании примером такой структуры может служить организационная структура глобальной сети Internet. В [9] приводится графическая интерпретация гетерархической структуры (рисунок, г).
В классическом понимании иерархии по Саймону [8] глобальная цель системы декомпозируется на последовательность подцелей, тогда последовательное достижение совокупности подцелей приводит к достижению полной (глобальной) цели. Такая иерархия целей довольно часто ранее применялась для решения сложных задач. Однако в сложной системе вполне может возникнуть ситуация, когда взаимодействуют элементы внутри подсистемы, структурно подчиненной типу слой по [6].
Именно появление подсистем со своей оргструктурой, акцентом на самоуправление, динамичность, возможность функционировать в автономном режиме и необходимость учета так называемого человеческого фактора доказывает наличие и необходимость исследования гетерархической структуры в сложной системе.
Теоретико-множественный подход к формализации
Итак, примем, что сложная система описывается гетерархической структурой. Тогда сложная проблема принятия решения может быть представлена в виде семейств последовательно расположенных более простых подпроблем, решение которых позволит решить и исходную более простыми моделями и методами. Для чего предлагается разбивать первоначально высокий уровень неопределенности в системе к множеству более мелких неопределенностей путем ввода интервального оценивания.
Такую иерархию проблем называют иерархией слоев принятия решений, а всю систему – многослойной системой принятия решений [6]. Достижение цели в системе можно представить как совокупность вертикально расположенных решающих подсистем (или ситуаций) Si, т.е. иерархия типа «дерево», что проиллюстрировано в [4].
а б в г
Виды иерархий: а – доминантная полная; б – доминантная неполная; в – холархия; г – гетерархическая
Возможны два вида иерархии: элементы нижестоящего уровня строго различимы и подчиняются лишь вышестоящему элементу, и элементы нижестоящего уровня могут пересекаться между собой, т.е. мы рассматриваем так называемые сильные и слабые иерархии, которые можно определить как доминантно полные и неполные иерархии.
В этих случаях каждая из таких ситуаций может быть и отображением Si: Gi →G i–1, и решающим элементом. А именно, заданы множество решаемых задач Di(γi), γi ∈ Gi и преобразование Ti, такое, что для любого входа γi выход γi-1 = Si(γi) определяется функцией γi-1 = Ti(xi), где xi – решение задачи Di(γi). Таким образом, входы γi выступают в качестве параметров (задаваемых непосредственно вышестоящим элементом), конкретизирующих решаемые задачи в Si; соответственно, выходы γi-1, получающиеся после применения преобразования Ti, являются в свою очередь параметрами, задаваемыми непосредственно нижестоящему элементу [6].
Алгоритм
Если отклонение состояния субъекта от желаемой динамики, например, по признаку yq «исход взаимодействия» описывается нечетким интервалом, то предлагается определять максимизирующее управление для следующего шага принятия решения с помощью разработанного алгоритма.
Введем следующие обозначения: признак управления «исход взаимодействия» обозначим лингвистической переменной yq; тогда на Ii уровне иерархии набор признаков – 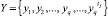 ; результат взаимодействия систем в некоторый момент времени tj опишем нечетким интервалом
; результат взаимодействия систем в некоторый момент времени tj опишем нечетким интервалом 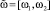 ,
, 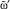 – вспомогательная переменная;
– вспомогательная переменная; 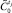 и
и 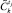 – соответственно текущее и эталонное состояния управляемой системы в момент tj, описываемые набором признаков Y;
– соответственно текущее и эталонное состояния управляемой системы в момент tj, описываемые набором признаков Y; 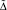 – величина отклонения признака после применения воздействия с целью достижения траектории нарастания нужного для системы качества;
– величина отклонения признака после применения воздействия с целью достижения траектории нарастания нужного для системы качества; 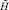 – искомая величина воздействия такая, что управление не изменяет силу воздействия по сравнению с предыдущим моментом управления; искомое множество Парето оптимальных исходов множества
– искомая величина воздействия такая, что управление не изменяет силу воздействия по сравнению с предыдущим моментом управления; искомое множество Парето оптимальных исходов множества 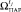 для момента tj.
для момента tj.
1. Представить нечеткий интервал 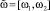 , которым описывается результат взаимодействия систем в некоторый момент tj, с помощью нечеткого множества
, которым описывается результат взаимодействия систем в некоторый момент tj, с помощью нечеткого множества 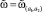 , где a1 – стратегия управляющей системы, a2 – стратегия управляемой системы. Если ω1 и ω2 заданы на шкалах разной размерности, для представления нечеткого множества на единой шкале, воспользуемся масштабирующими коэффициентами, определяемыми согласно правилу
, где a1 – стратегия управляющей системы, a2 – стратегия управляемой системы. Если ω1 и ω2 заданы на шкалах разной размерности, для представления нечеткого множества на единой шкале, воспользуемся масштабирующими коэффициентами, определяемыми согласно правилу
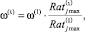
где 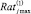 - размерность шкалы для оценки признака при применении «слабых» воздействий определяется с помощью суммарного рейтингового числа по всем видам управлений:
- размерность шкалы для оценки признака при применении «слабых» воздействий определяется с помощью суммарного рейтингового числа по всем видам управлений:
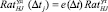 .
.
Для определения 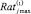 – размерности шкалы для оценки признака при применении воздействий с силой i, используется операция дополнительного вычитания (–) нечетких чисел.
– размерности шкалы для оценки признака при применении воздействий с силой i, используется операция дополнительного вычитания (–) нечетких чисел.
2. Если предыдущее состояние управляемой системы 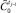 описано в виде нечеткого интервала [ω1 , ω2 ], то представить его в виде нечеткого множества, воспользовавшись функциями принадлежности
описано в виде нечеткого интервала [ω1 , ω2 ], то представить его в виде нечеткого множества, воспользовавшись функциями принадлежности 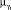 и
и 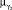 термов лингвистической переменной yq. Если ω1 и ω2 заданы на шкалах разной размерности для представления нечеткого множества на единой шкале, воспользоваться масштабирующими коэффициентами.
термов лингвистической переменной yq. Если ω1 и ω2 заданы на шкалах разной размерности для представления нечеткого множества на единой шкале, воспользоваться масштабирующими коэффициентами.
3. Выполнить сложение 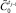 и нечеткого исхода по отдельному признаку
и нечеткого исхода по отдельному признаку  для определения текущего состояния
для определения текущего состояния 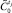 управляемой системы:
управляемой системы: 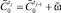 .
.
4. Выполнить нормализацию 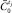 , т.е. представить его на интервале [0, 1].
, т.е. представить его на интервале [0, 1].
5. Определить, имеет ли место отклонение текущего состояния 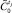 от эталонного состояния
от эталонного состояния 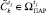 для момента tj. Отклонения нет, если в
для момента tj. Отклонения нет, если в 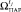 имеется хотя бы один элемент
имеется хотя бы один элемент 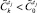 , где
, где 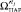 - суженное множество Парето W для момента времени tj.
- суженное множество Парето W для момента времени tj.
6. Исходы из 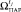 , являющиеся нечетким интервалом [ω1 , ω2 ], представить в виде нечеткого множества. Для представления воспользоваться функциями принадлежности
, являющиеся нечетким интервалом [ω1 , ω2 ], представить в виде нечеткого множества. Для представления воспользоваться функциями принадлежности 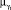 и
и 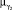 термов лингвистической переменной yq. Если ω1 , ω2 заданы на шкалах разной размерности, для представления нечеткого множества на единой шкале воспользуемся масштабирующими коэффициентами.
термов лингвистической переменной yq. Если ω1 , ω2 заданы на шкалах разной размерности, для представления нечеткого множества на единой шкале воспользуемся масштабирующими коэффициентами.
7. Сравнить 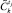 и
и 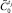 для определения, имеет ли место отклонение: ≤ или ≥ от эталонного состояния
для определения, имеет ли место отклонение: ≤ или ≥ от эталонного состояния  для момента tj. Отклонения нет, если в
для момента tj. Отклонения нет, если в 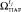 имеется хотя бы один элемент
имеется хотя бы один элемент 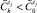 , для выяснения этого выполняются следующие действия:
, для выяснения этого выполняются следующие действия:
7.1. Выяснить, сколько исходов содержит 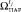 . Если один исход, то
. Если один исход, то 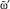 присвоить этот исход и включить переход к п. 7.3; иначе
присвоить этот исход и включить переход к п. 7.3; иначе 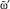 присвоить первый элемент
присвоить первый элемент 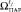 и переход к п. 7.3.
и переход к п. 7.3.
7.2. Представить нечеткий интервал, которым описывается 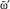 , в виде нечеткого множества.
, в виде нечеткого множества.
7.3. Сравнить нечеткие множества с параметрами 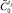 и
и 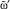 для момента управления tj.
для момента управления tj.
7.4. Если результат процедуры сравнения в п. 7.3 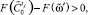 то
то 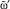 внести в Ω′ и перейти к п. 7.6; иначе переход к п. 7.5.
внести в Ω′ и перейти к п. 7.6; иначе переход к п. 7.5.
7.5. Выяснить, существуют ли еще в 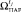 не сравнивавшиеся исходы. Если «да», то
не сравнивавшиеся исходы. Если «да», то 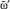 присвоить еще не сравнивавшийся исход из
присвоить еще не сравнивавшийся исход из 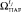 и переход к п. 7.2; иначе – присвоить
и переход к п. 7.2; иначе – присвоить 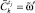 , преобразовать нечеткий интервал, которым описывается
, преобразовать нечеткий интервал, которым описывается 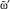 в виде нечеткого множества. Спрогнозировать возможность достижения
в виде нечеткого множества. Спрогнозировать возможность достижения 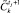 по
по 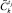 и переход к п. 14 для текущего класса управления i, результат прогноза –
и переход к п. 14 для текущего класса управления i, результат прогноза – 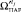 . Определяется возможность достижения состояний
. Определяется возможность достижения состояний 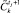 и
и 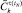 как
как 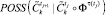 и
и 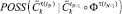 соответственно при применении управления силы t в моменты времени tj или tN–1.
соответственно при применении управления силы t в моменты времени tj или tN–1.
7.6. Присвоить 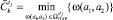 .
.
8. Зафиксировать текущую силу воздействия i как приводящую к минимальной величине исхода, поскольку нет отклонения от эталонного признака в момент tj.
9. Произвести выбор ветви иерархии для представителей текущего класса управляемой системы с текущей силой воздействия i для момента tj+1.
10. Найти минимальный элемент в 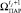 [2]. Результат –
[2]. Результат – 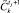 .
.
11. Спрогнозировать, описано в [2], возможность достижения 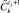 по
по 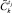 для класса управлений i. Из процедуры прогноза возвращается
для класса управлений i. Из процедуры прогноза возвращается 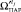 ,
, 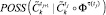 ,
, 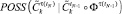 , переход к п. 17.
, переход к п. 17.
12. Определить величину отклонения 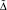 по [2].
по [2].
13. Найти минимальный элемент 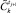 в
в 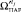 [2]. Результат –
[2]. Результат – 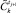 . Преобразовать нечеткий интервал, которым описывается
. Преобразовать нечеткий интервал, которым описывается 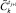 , в нечеткое множество.
, в нечеткое множество.
14. Выполнить сложение 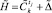 . Для этого воспользуемся операцией суммирования с использованием уровневых множеств.
. Для этого воспользуемся операцией суммирования с использованием уровневых множеств.
15. Определить элемент 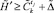 в множестве
в множестве 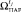 . Если в процессе определения выяснено, что
. Если в процессе определения выяснено, что  отсутствует, то переход к п. 19; иначе к п. 16.
отсутствует, то переход к п. 19; иначе к п. 16.
16. Спрогнозировать, описано в [2], возможность достижения 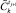 по
по  для текущего класса управления i. Из процедуры прогноза возвращается
для текущего класса управления i. Из процедуры прогноза возвращается 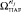 ,
, 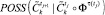 ,
, 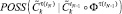 .
.
17. Запросить лицо, принимающее решение (ЛПР), об удовлетворенности, найденной возможности достижения 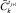 по
по  в п. 16. Если «да», то переход к п. 18, иначе к п. 19.
в п. 16. Если «да», то переход к п. 18, иначе к п. 19.
18. Запросить ЛПР об удовлетворительности 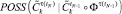 . Если «да», то в момент tj+1 использовать управление, давшее результат в п. 16 и переход к п. 23; иначе переход к п. 19.
. Если «да», то в момент tj+1 использовать управление, давшее результат в п. 16 и переход к п. 23; иначе переход к п. 19.
19. Проанализировать предыдущие ветви иерархии, отвечающие предыстории процесса и характеризующиеся различной силой управления i, и выяснить, существуют ли ветви иерархии, моделирующие силу управления i = i + 1.
19.1. Если такие ветви найдутся, то увеличить на 1 силу управления i = i + 1 и перейти к п. 19.2.; иначе переход к п. 21.
19.2. Промоделировать ситуацию с новой силой управления t. Результатом является множество Парето-оптимальных исходов 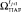 .
.
19.3. Исходы из 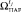 , являющиеся нечетким интервалом [ω1, ω2], представить его в виде нечеткого множества. Для представления воспользоваться функциями принадлежности
, являющиеся нечетким интервалом [ω1, ω2], представить его в виде нечеткого множества. Для представления воспользоваться функциями принадлежности 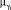 и
и 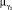 термов лингвистической переменной yq. Если ω1 и ω2 заданы на шкалах разной размерности для представления нечеткого множества на единой шкале, воспользоваться масштабирующими коэффициентами.
термов лингвистической переменной yq. Если ω1 и ω2 заданы на шкалах разной размерности для представления нечеткого множества на единой шкале, воспользоваться масштабирующими коэффициентами.
19.4. Найти 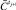 с минимальным значением в
с минимальным значением в 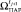 [2].
[2].
20. Определить возможность достижения ближайшего эталонного состояния 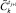 по
по 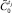 или
или 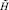 для текущего класса управлений i, описано в [2]. Если
для текущего класса управлений i, описано в [2]. Если 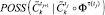 удовлетворяет ЛПР, то переход к п. 18; иначе переход к п. 19.
удовлетворяет ЛПР, то переход к п. 18; иначе переход к п. 19.
21. Определить эталонное состояние 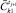 минимально меньше
минимально меньше 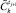 по признаку yq.
по признаку yq.
21.1. Присвоить класс k1 самому «слабому» по способности к приобретению нужного качества на уровне иерархии Ii.
21.2. Сравнить 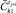 и
и 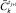 .
.
21.3. Присвоить 
21.4. Присвоить класс k2 более «высокому» по способности к приобретению нужного качества на уровне иерархии Ii.
21.5. Если 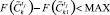 , то переход к п. 21.3; иначе выяснить, существуют ли более «высокие» по способностям к приобретению нужного качества классы. Если да, то переход к п. 21.4; иначе переход к п. 22.
, то переход к п. 21.3; иначе выяснить, существуют ли более «высокие» по способностям к приобретению нужного качества классы. Если да, то переход к п. 21.4; иначе переход к п. 22.
22. Выполнить пп. 5–16 с вновь установленной принадлежностью к классу k = k1 или k = k2 в зависимости от результатов п. 21 исследуемого уровня иерархии Ii на основе найденного максимального значения.
23. Конец.
Заключение
В данной статье предлагается использовать гетерархическую структуру для описания модели сложной системы в виде нечеткой ситуационной сети. Представленный в данной статье алгоритм претендует на достижение решения за конечное время, а его отличительной чертой является возможность уточнения решения в ходе самого решения, что позволяет соотнести его с эволюционным моделированием. В качестве цели возможно использовать не единственное, а набор альтернативных решений, а эталонное состояние определять как набор признаков. Интервальное оценивание учитывает показатели различной природы, силу связи и позволяет проводить качественный анализ.
Работа выполнена при финансовой поддержке гранта РФФИ № 16-07-00335 «Иерархическая организация нейроэволюционных вычислений».



