Мультипроектное планирование решает взаимосвязанные проблемы – формирование календарного графика [2] и распределение ресурсов [1, 11]. Календарные графики мультипроектного планирования являются расписаниями иерархических или сетевых структур действий [3, 5, 6]. Проекты могут быть технологически независимыми, но объединенными по потребляемым ресурсам. Для описания комплекса работ проекта необходимо наличие описание каждой работы. Трудоемкость (продолжительность) работ измеряется в тактах планирования. Потребности отдельных работ в ресурсах измеряются условными единицами на такт планирования. Работы проектов выполняются с постоянной интенсивностью [1]. Каждый тип ресурса однороден.
Формирование расписания – это определение времен начала выполнения всех действий или их совокупностей в интервале расписания [8]. Для мультипроектного планирования необходимо решение двух задач:
1) агрегирование заявок проекта – определение относительных начальных времен выполнения каждой работы в пределах интервала расписания проекта (длительности критического пути графа проекта или задаваемой/переопределяемой длительности);
2) формирование календарного графика мультипроектного планирования – определение относительных начальных времен выполнения агрегаций заявок проектов в пределах задаваемого или определяемого интервала расписания.
Предполагается, что агрегации всех проектов мультипроекта известны [4].
Статья посвящена решению второй задачи, а ее целью является представление подходов к программному формированию расписания (календарного графика) для произвольного количества сетей заявок (агрегаций заявок проектов) в системе с однородными ресурсами.
Общие подходы
При алгоритмизации и разработке программного обеспечения формирования календарных графиков мультипроектного планирования использованы следующие концепции [3]: программное решение задачи в рамках СУБД; двухэтапный процесс решения; идеология жадного алгоритма; концепции загруженности и равномерности; использование методов ранжирования теории принятия решений.
Два этапа решения включают формирование начального календарного плана и его последующую оптимизацию. Под начальным календарным графиком будет пониматься любой программно сформированный календарный график, соблюдающий обязательные ограничения. Методы этапов цикличны и завершаются после включения всех проектов в начальный календарный план или при невозможности дальнейшего улучшения плана.
Формирование начального календарного плана решается последовательным выбором очередного проекта и последующим его включением в календарный график в определяемое время начала выполнения проекта. Выбор проекта базируется на концепции загруженности, то есть на каждом шаге определяется наиболее загруженный по требуемым ресурсам проект. Выбор времени включения этого проекта использует концепцию равномерности. В каждом цикле присутствуют две операции выбора с принятием некоторых решений.
Задача оптимизации начального календарного плана решается последовательным выбором наиболее неравномерного проекта и последующей его перестановкой в выбираемое время начала выполнения проекта. Перестановка проекта в календарном графике базируется на концепции равномерности. В каждом цикле также присутствуют две операции выбора. Такой подход характерен для жадных алгоритмов [7, 11], предполагающих цикличность обоих этапов задачи формирования календарного плана [7].
Операции выбора в представляемых алгоритмах многокритериальны [9], и для их реализации привлечен аппарат методов ранжирования. Операции выбора используют метод «жесткого» ранжирования [10]. В дальнейшем под термином многокритериальное ранжирование будет пониматься «жесткое» ранжирование. Будут различаться прямое (по «возрастанию») и обратное (по «убыванию») многокритериальное ранжирование.
Постановка и формализация задачи
Введем необходимые в дальнейшем обозначения.
Исходные данные задачи:
I – количество проектов мультипроектного планирования;
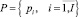 – множество проектов мультипроекта;
– множество проектов мультипроекта;
индекс проекта 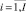 имеет различный характер в зависимости от решаемой задачи: идентификатор проекта в соответствующей таблице БД; порядковый номер проекта при его включении в начальный календарный график; порядковый номер проекта при оптимизации начального календарного графика;
имеет различный характер в зависимости от решаемой задачи: идентификатор проекта в соответствующей таблице БД; порядковый номер проекта при его включении в начальный календарный график; порядковый номер проекта при оптимизации начального календарного графика;
nei – количество работ проекта pi;
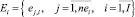 – множество работ проекта pi (j = 1 – источник, j = nei – сток);
– множество работ проекта pi (j = 1 – источник, j = nei – сток);
индекс работы 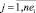 также имеет различный характер в зависимости от решаемой задачи: идентификатор работы в соответствующей таблице БД; идентификатор работы в множестве работ проекта; идентификатор работы в множестве работ пути графа проекта;
также имеет различный характер в зависимости от решаемой задачи: идентификатор работы в соответствующей таблице БД; идентификатор работы в множестве работ проекта; идентификатор работы в множестве работ пути графа проекта;
u – количество типов возобновляемых ресурсов;
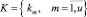 – множество типов возобновляемых ресурсов;
– множество типов возобновляемых ресурсов;
Rm,i, 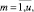
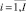 – объем ресурса типа km, выделяемый проекту pi во время его выполнения на каждом такте планирования;
– объем ресурса типа km, выделяемый проекту pi во время его выполнения на каждом такте планирования;
rm,j,i, 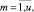
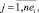
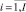 – объем ресурса типа km, требуемый работе ej,i проекта pi во время ее выполнения на j-м такте планирования;
– объем ресурса типа km, требуемый работе ej,i проекта pi во время ее выполнения на j-м такте планирования;
dj,i, 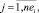
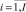 – длительность (трудоемкость) выполнения работы ej,i проекта pi;
– длительность (трудоемкость) выполнения работы ej,i проекта pi;
Int – интервал расписания – длительность календарного графика в тактах планирования.
Исходные расчетные данные задачи:
npi, 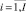 – количество путей графа сети проекта pi;
– количество путей графа сети проекта pi;
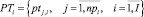 – множество путей графа сети проекта pi;
– множество путей графа сети проекта pi;
Cpi, 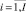 – критический путь проекта pi, такты планирования;
– критический путь проекта pi, такты планирования;
nepj,i, 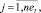
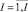 – количество работ пути pi,j графа сети проекта pi;
– количество работ пути pi,j графа сети проекта pi;
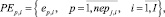
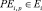 – множество работ пути ptj,i графа сети проекта pi;
– множество работ пути ptj,i графа сети проекта pi;
Di – длительность (трудоемкость) выполнения проекта pi в тактах планирования. В предлагаемом решении принято Di = Cpi, 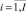 .
.
Переменные задачи:
ni, 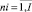 – количество: включенных в начальный календарный график проектов; оптимизированных (переставленных) проектов в календарном графике;
– количество: включенных в начальный календарный график проектов; оптимизированных (переставленных) проектов в календарном графике;
nr, 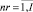 – количество: не включенных в начальный календарный график проектов; не оптимизированных проектов в календарном графике;
– количество: не включенных в начальный календарный график проектов; не оптимизированных проектов в календарном графике;
Rmaxm, 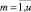 – максимальная величина тактового потребления ресурса типа km в календарном графике;
– максимальная величина тактового потребления ресурса типа km в календарном графике;
TIi – начальный такт планирования для выполнения проекта pi в календарном графике;
TFi = TIi + Di – финальный такт планирования проекта pi в календарном графике;
rpm,j,i, 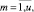
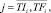
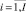 – объем ресурса типа km, потребляемый проектом pi на j-м такте интервала расписания;
– объем ресурса типа km, потребляемый проектом pi на j-м такте интервала расписания;
RSm,j, 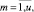
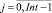 – объем ресурса типа km, потребляемый календарным графиком на j-м такте интервала расписания;
– объем ресурса типа km, потребляемый календарным графиком на j-м такте интервала расписания;
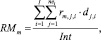
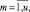
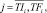
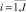 – средний объем ресурса типа km, потребляемый проектами календарного графика на каждом такте интервала расписания;
– средний объем ресурса типа km, потребляемый проектами календарного графика на каждом такте интервала расписания;
RPm,j,i, 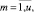
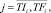
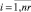 – оценка равномерности j-го такта проекта pi по ресурсу типа km;
– оценка равномерности j-го такта проекта pi по ресурсу типа km;
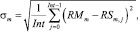
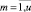 – среднеквадратичное отклонение потребления ресурса типа km от среднего значения в интервале расписания.
– среднеквадратичное отклонение потребления ресурса типа km от среднего значения в интервале расписания.
Задача формирования начального календарного графика решается пошаговым выбором очередного проекта и формированием расписания 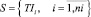 , которое минимизирует вектор максимальных величин потребления ресурсов в интервале расписания
, которое минимизирует вектор максимальных величин потребления ресурсов в интервале расписания
min(Rmax1, Rmax2, ..., Rmaxu), (1)
при обязательных ограничениях
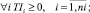
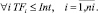 (2)
(2)
Целевая функция (1) обеспечивает минимизацию верхнего ограничения отклонений, что достаточно для формирования начального календарного графика при включении очередного проекта в график. Целевая функция связана с необходимостью многокритериального ранжирования получаемых векторов (1). Формирование начального календарного графика завершается исчерпанием списка не включенных в график проектов (nr = 0). Неравенства ограничений (2) отражают безусловность нахождения проектов в интервале расписания.
Оценка загруженности cj,m,i работы ej,i не включенного в календарный график проекта pi на очередном шаге формирования начального календарного графика определяется объемом требуемого в период выполнения работы ресурса
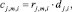
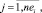
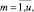
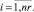 (3)
(3)
Чем больше величина оценки (3), тем более соответствующая работа ej,i проекта pi загружена по ресурсу типа km. Оценки (3) формируют множество векторов (критериев загруженности) работ на очередном шаге формирования начального календарного графика
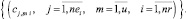 (4)
(4)
Обратное многокритериальное ранжирование векторов (4) порождает множество рангов
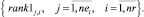 (5)
(5)
Ранги работ (5) формируют множество векторов (критериев загруженности) путей графов сетей проектов
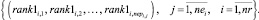 (6)
(6)
Обратное многокритериальное ранжирование векторов (6) порождает множество рангов критериев загруженности путей графов сетей проектов
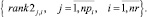 (7)
(7)
Ранги векторов (7) формируют множество векторов (критериев загруженности) проектов
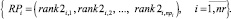 (8)
(8)
Старший по рангу проект, полученный прямым многокритериальным ранжированием векторов (8), является самым загруженным при принятых оценках и критериях загруженности. Он становится очередным кандидатом pni+1 на включение в начальный календарный график.
Для определения начального времени включения TIni+1 проект pni+1 последовательно, по одному такту перемещается с учетом ограничений (2) внутри интервала расписания Int, формируя множество векторов:
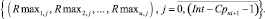 (9)
(9)
Прямое многокритериальное ранжирование векторов (9) определяет доминирующий вектор, индекс j которого определяет искомое начальное время включения проекта pni+1 в начальный календарный график TIni+1 = j. Если nr > 0, то переход к следующему шагу формирования начального календарного графика.
Задача оптимизации начального календарного графика состоит в изменении начального расписания для формировании расписания 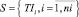 , которое минимизирует вектор среднеквадратичных отклонений потребления ресурсов
, которое минимизирует вектор среднеквадратичных отклонений потребления ресурсов 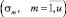 от средних значений в интервале расписания
от средних значений в интервале расписания
min(σ1, σ2, ..., σu), (10)
при обязательных ограничениях (2).
Целевая функция (10), являясь интегральной оценкой календарного графика, минимизирует все отклонения. Целевая функция связана с необходимостью многокритериального ранжирования получаемых на ее основе векторов (10). Завершение процесса оптимизации начального календарного графика обусловлено принимаемой стратегией действий.
Оценка равномерности j-го такта проекта pi по ресурсу km на очередном шаге оптимизации начального календарного графика определяется следующим выражением:
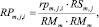
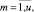
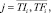
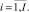 (11)
(11)
Значения тактовых оценок равномерности находятся в интервале [0, 1]. Чем больше величина оценки (11), тем неравномернее соответствующий проект на данном такте интервала расписания по данному ресурсу. Оценки равномерности проектов (11) формируют u множеств векторов (критериев равномерности) проектов по каждому ресурсу.
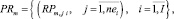
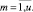 (12)
(12)
Прямое многокритериальное ранжирование векторов (12) проектов расписания порождает множества рангов векторов проектов по каждому ресурсу
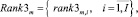
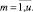 (13)
(13)
Ранги векторов (13) формируют множество векторов (критериев равномерности) неоптимизированных проектов
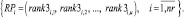 (14)
(14)
Старший по рангу проект, полученный прямым многокритериальным ранжированием векторов (14), является самым неравномерным среди неоптимизированных при принятых оценках и критериях равномерности. Он становится очередным кандидатом pni+1 на перестановку в календарном графике.
Для определения начального времени TIni+1 перестановки проект pni+1 последовательно, по одному такту перемещается с учетом ограничений (2) внутри интервала расписания Int, формируя множество векторов:
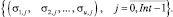 (15)
(15)
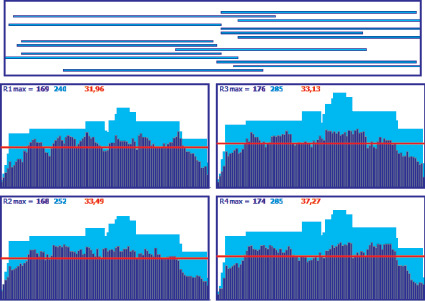
Рис. 1. Начальный календарный график
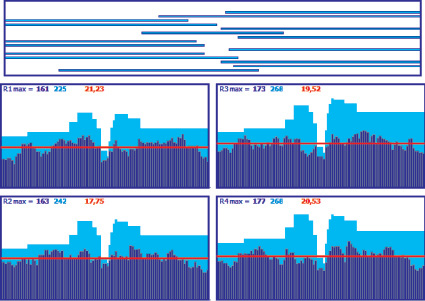
Рис. 2. Оптимизированный календарный график
Прямое многокритериальное ранжирование векторов (15) определяет доминирующий вектор, индекс j которого определяет начальное время TIni+1 = j для перестановки проекта pni+1 в календарном графике. Если nr > 0, то переход к следующему шагу оптимизации.
Результаты исследования и их обсуждение
Для численных экспериментов использовалось тестовое задание, включающее I = 15 проектов, случайно выбранных из библиотеки тестовых задач PSPLib [12]. Проекты включают по 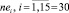 работ, и им требуется 4 типа ресурсов (u = 4).
работ, и им требуется 4 типа ресурсов (u = 4).
На рис. 1 представлены результаты формирования начального календарного графика мультипроектного планирования при принятых агрегациях проектов [4]. В верхней части рисунка представлена диаграмма Гантта для 15 проектов тестового задания при принятом интервале расписания в 100 тактов планирования. В нижней части показаны диаграммы потребления (синий цвет) и выделения (голубой цвет) каждого из четырех ресурсов на каждом такте планирования. Цифрами в диаграммах ресурсов представлены максимальные значения тактового потребления и выделения ресурса. Третья цифра показывает среднеквадратичное отклонение от среднего значения в процентах.
Анализ начального (рис. 1) и оптимизированного (рис. 2) календарных графиков:
1) уменьшение значений среднеквадратичных отклонений в оптимизированном календарном графике;
2) использование целевой функции (10) дало побочный эффект – снижение значений максимальных величин тактового потребления и выделения ресурсов;
3) повышение уровня потребления ресурсов у границ интервала расписания и, как следствие, смещение большинства проектов (рис. 2) к границам интервала расписания.
Таким образом, представлены следующие результаты:
- осуществлена формализация задачи формирования и оптимизации календарного графика для сетевых моделей исходных требований;
- представлены общие подходы и алгоритмы решения задач формирования календарных графиков с использованием методов ранжирования теории принятия решений;
- визуализированы результаты формирования календарных графиков.



