Цель исследования. В условиях формирования глобального образовательного пространства (Болонский процесс следует рассматривать как этап реализации этой тенденции, решающей проблему применительно к европейскому региону) актуален переход в системах профессионального образования от объект-субъектных отношений к объект-объектным. Такой переход в качестве одной из целей выдвигает разработку и применение научно-учебно-методических средств поддержки самостоятельной работы студентов при их подготовке к профессиональной деятельности (как в рамках получения первоначального профессионального образования различного уровня, так и при повышении квалификации, переподготовке, освоении новой специальности).
Целью исследования, основные результаты которой представлены в статье, была разработка модуля, обеспечивающего освоение символического метода анализа цепей переменного тока (раздел, предусмотренный в общепрофессиональных дисциплинах практически для всех технических направлений и специальностей) и формирование навыков (компетенций) применения метода для расчета многоконтурных электрических цепей.
Результаты исследования и их обсуждение
При разработке модуля важно было обеспечить возможность освоения символического метода (на уровне понимания теории и получения навыка оперирования для типовых задач) даже студентами со слабой исходной физико-математической подготовкой. Для решения этой задачи теоретическая часть модуля включает информацию по прикладному применению комплексных чисел (на этом, собственно, основан символический метод). Значительное количество примеров позволяет усвоить принципы трансформации различных методов анализа, используемых для решения задач в цепях постоянного тока, и эффективного применения этих методов (трансформированных) при анализе цепей переменного тока.
Модуль содержит теоретическую часть [1, 3, 4], в которую включены основные понятия и определения, основы комплексного метода расчета электрических цепей, законы Ома и Кирхгофа в комплексной форме, методы расчета сложных электрических цепей синусоидального тока при установившихся процессах и иллюстрационные примеры применения этих методов. Окно раздела «Теоретические основы» представлено на рис. 1.
Степень усвоения теоретических положений пользователь может проверить, выполнив тестовые задания. Содержание и количество тестов подобрано так, чтобы при успешном результате можно было считать подготовленность на уровне не только понимания, но и умения применять знания для выполнения типовых заданий. Демоверсия тестового задания представлена на рис. 2.
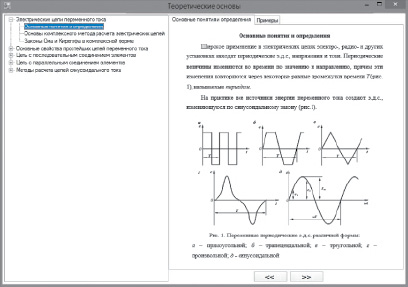
Рис. 1. Раздел «Теоретические основы»
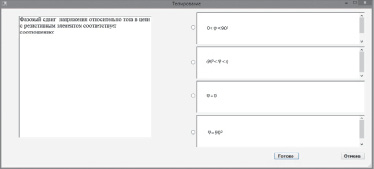
Рис. 2. Демоверсия тестового задания
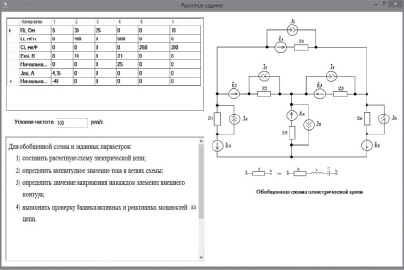
Рис. 3. Пример расчетного задания
После изучения теоретической части и успешного результата тестирования студент автоматически получает доступ к индивидуализированному заданию на выполнение расчета трехконтурной цепи (здесь речь идет об автономных, т.е. непересекающихся контурах). Пример расчетного задания представлен на рис. 3. Следует отметить, что стохастическое формирование структуры цепи и параметров элементов этой цепи исключает возможность выдачи одинаковых вариантов задания.
При выполнении первого пункта задания студент должен составить расчетную схему по своему варианту, исключив из обобщенной схемы элементы с нулевыми параметрами. После преобразования в цепи останутся один или два источника тока, но при анализе цепи удобно вместо источников тока использовать эквивалентные источники эдс. Для преобразования источника энергии в эквивалентный используют следующую формулу:
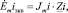
где i – номер ветви; Jmi – значение источника тока в ветви с номером i; 
– полное сопротивление ветви с номером i.
Во втором пункте расчетного задания необходимо определить амплитудные значения токов в ветвях схемы. Для расчетной схемы, которая содержит три автономных контура, удобнее воспользоваться методом контурных токов.
Для определения токов в ветвях методом контурных токов студент должен решить систему контурных уравнений и найти контурные токи. Общий вид системы контурных уравнений для трехконтурной цепи:
где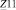 
, 
, 
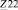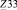– собственные сопротивления первого, второго, и третьего контуров соответственно;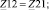 
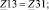
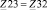– смежные сопротивления между первым и вторым, первым и третьим, вторым и третьим контурами соответственно; E11, E22, E33 – контурные эдс первого, второго и третьего контуров соответственно; 
, 
, 
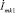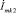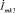– контурные токи первого, второго, и третьего контуров соответственно.
По результатам расчета контурных токов легко найти значения токов в ветвях анализируемой цепи. Например, ток в первой ветви (номер ветви совпадает с цифрой в буквенно-цифровом обозначении элементов входящих в ветвь) для параметров цепи приведенных на рис. 3 равен
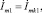
т.к. в первой ветви действует только первый контурный ток.
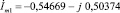(A).
Значение модуля амплитуды тока в первой ветви
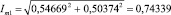(A).
При выполнении третьего пункта задания амплитудные значения источников энергии, входящих во внешний контур, уже известны, и для того, чтобы определить их действующие значения, нужно воспользоваться следующим соотношением:
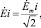
где i – номер ветви.
Для определения напряжения на остальных элементах, входящих во внешний контур, надо вычислить предварительно действующие значения и начальные фазы соответствующих токов. После этого определяем напряжения на резисторах, конденсаторах и катушках индуктивности по следующим формулам:
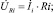
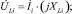
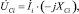
где i – номер ветви; 
– комплекс действующего значения тока в ветви с номером i; Ri – сопротивление резистора в ветви с номером i; XLi – сопротивление катушки индуктивности в ветви с номером i; XCi – сопротивление конденсатора в ветви с номером i.
В пятом пункте расчетного задания нужно выполнить проверку баланса мощностей. При оперировании с мощностями используют средние квадратические значения величин. В предыдущих пунктах задания определены комплексы действующих значений токов не для всех ветвей, поэтому перед выполнением проверки баланса мощностей необходимо определить модули и аргументы по недостающей информации. После этого можно посчитать полную мощность (
), потребляемые активную (PПОТ) и реактивную (QПОТ) мощности.
Относительная погрешность по активной составляющей баланса мощности рассчитывается по следующей формуле:
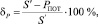
где S′ – вещественная составляющая полной мощности 
.
Относительная погрешность по реактивной составляющей баланса мощности рассчитывается по следующей формуле:
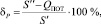
где S″ – мнимая составляющая полной мощности 
.
На любом этапе по запросу студент может получить помощь в виде, например, конкретного расчета по интересующему его методу.
Достоверность выполненного расчета можно проверить по результатам сопоставления значений токов в ветвях, полученных разными методами анализа. Кроме того, для метода контурных токов предусмотрена заданием проверка баланса мощностей (активной, реактивной и полной). Окно с результатами проверки баланса мощностей (параметры цепи см. на рис. 3) представлено на рис. 4.
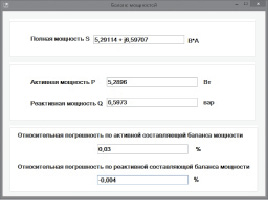
Рис. 4. Проверка баланса мощностей
Проверка выполнения энергетического баланса (баланса мощностей) электрических цепей прежде всего представляет интерес как частный случай реализации одного из фундаментальных законов – закона сохранения энергии. Но это одновременно и эффективный способ контроля достоверности результатов анализа используемых методов расчета электрической цепи. Если при оперировании с числовыми значениями при решении варианта задания выполнены вычисления с учетом четырех знаков в дробной части, то различие генерируемой мощности и потребляемой, оцениваемое по относительной погрешности, не превысит десятых долей процента (показатель, приемлемый для многих инженерных расчетов электрических цепей).
Для всех методов анализа, которые предусмотрены в расчетной части задания, алгоритм автоматизированного решения реализован в среде MS Visual Studio [2, 5]. Доступ к этой части программы имеет только преподаватель. По своему варианту задания студент может ввести конечные результаты и по конкретному методу получить информацию о достоверности (или недостоверности) этих результатов.
Если задание выполнено правильно, то студент получает сообщение о том, что это задание зачтено. При наличии ошибок ему предлагается самостоятельно перепроверить решение и устранить выявленные недостатки. После повторного запроса студента по конкретному варианту задания (когда вторично результат анализа, выполненного студентом, не соответствует частично или полностью достоверным итогам) студент получает уведомление о необходимости явиться на консультацию к преподавателю в предусмотренные расписанием контактные часы.
Выводы
Модуль предоставляет возможность изучать теорию методов анализа в удобном для пользователя темпе, либо (если студент уже имеет соответствующую подготовку) непосредственно перейти к этапу тестирования с последующим получением индивидуального задания.
Совокупность указанных особенностей модуля позволяет рекомендовать его в состав учебно-методического сопровождения по специальностям и направлениям, в которых предусмотрено освоение методов анализа электрических однофазных цепей синусоидального тока.