В настоящее время во многих учебных заведениях мира среди преподавателей и студентов широкое распространение получила система компьютерной математики Maple, разработанная в 1980 году группой исследователей канадского университета Waterloo. С момента появления программа постоянно совершенствуется. Командный язык пакета Maple прост и понятен, следует отметить быстроту в работе и экономное использование памяти, а также пакет Maple работает с большинством операционных систем, чем и объясняется его коммерческий успех.
Работа посвящена исследованию краевой задачи для уравнения эллиптического типа с оператором Бесселя с помощью качественной теории дифференциальных уравнений в частных производных, а также с помощью системы компьютерной математики Maple, которая является незаменимым помощником для преподавателей и студентов физико-математического направления.
Краевые задачи для уравнений в частных производных с оператором Бесселя рассматриваются в работах многих авторов [2; 3; 5] и представляют научный интерес. Результаты настоящей работы являются продолжением исследований задач математической физики для уравнений с оператором Бесселя.
Пусть
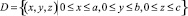
– область пространства Oxyz. Рассмотрим в области D эллиптическое уравнение вида
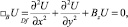(1)
где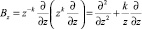 
– оператор Бесселя, 0 < k < 1 – заданное действительное число.
Требуется найти функцию U(x, y, z), удовлетворяющую условиям
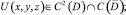(2)
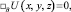(x, y, z) ∈ D; (3)
U(0, y, z) = 0; U(a, y, z) = 0; (4)
U(x, 0, z) = 0; U(x, b, z) = 0; (5)
Uz(x, y, 0) = 0; U(x, y, c) = φ(x, y). (6)
Введем уравнение (1) в программе Maple под именем eq:
> restart;
>eq:=diff(u(x,y,z),x$2)+diff(u(x,y,z),y$2)+diff(u(x,y,z),z$2)+(k/z)*diff(u(x,y,z),z)=0.
На экране синим цветом появится уравнение в виде
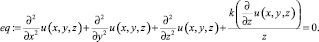
Построим систему частных решений уравнения (1), удовлетворяющих условиям (2), (4) и (5). Частное решение уравнения (1), согласно методу Фурье (метод разделения переменных), ищем в виде
U(x, y, z) = X(x)Y(y)Z(z), (7)
где X, Y и Z – пока неопределенные функции.
В программе команда разделения переменных и результат будут выглядеть так
>pdsolve(eq,HINT=X(x)*Y(y)*Z(z));
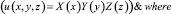
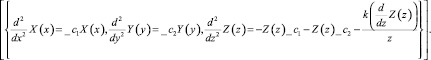
Анализируя результат, согласно [4], и подставляя функцию (7) в граничные условия (4) и (5), относительно неизвестной функции X(x) получаем задачу
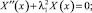(8)
X(0) = 0; X(a) = 0. (9)
Задача (8)–(9) – задача Штурма – Лиувилля, о нахождении нетривиальных решений уравнения (8), удовлетворяющих граничным условиям (9).
Относительно неизвестной функции Y(y) получаем следующую спектральную задачу
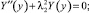(10)
Y(0) = 0; Y(b) = 0. (11)
А относительно функции Z(z) получили уравнение Бесселя:
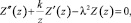(12)
где переменные разделения в уравнениях (8), (10) и (12) связаны соотношением
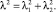(13)
Найдем в Maple решение уравнения (8), удовлетворяющее первому условию в (9):
>eq1:=diff(X(x),x$2)+(lambda(1))^2*X(x)=0;
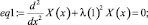
>dsolve({eq1,X(0)=0},X(x));
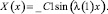
Так как собственные функции спектральной задачи определяются с точностью до постоянного множителя, примем значение константы C1 равным единице:
>sol1:= %;
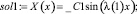
>subs(_C1=1,sol1);
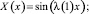
>_EnvAllSolutions:=true:
Теперь нужно найти неизвестный коэффициент λ(1), учитывая второе условие в (9).
>solve(sin(lambda(1)*a)=0,lambda(1));
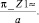
Таким образом, каждому собственному значению ν:
>nu:=n -> pi*n/a;
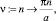
соответствует собственная функция вида
>X:=(x,n) -> sin(x*nu(n));
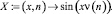
Следует пояснить для дальнейшего решения краевой задачи некоторые шаги вычислений программы. Общее решение уравнения (8) имеет вид
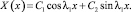(14)
Подставив функцию (14) в первое условие из (9), найдем, что C1 = 0, а константу C2, как уже пояснялось, положим равной единице.
С учетом второго граничного условия будем иметь
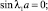
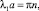n = ±1, ±2, ...
Таким образом, собственные значения задачи Штурма – Лиувилля (8)–(9) имеют вид
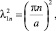n = 1, 2 ... (15)
А каждому собственному значению λ1n соответствует собственная функция
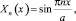n = 1, 2 ... (16)
С помощью команд
>eq2:=diff(Y(y),y$2)+(lambda(2))^2*Y(y)=0;
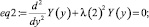
>dsolve({eq2,Y(0)=0},Y(y));
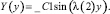
Следует отметить, что программа опять выводит константу _C1, считая ее уже новой.
>sol2:= %;
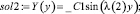
>subs(_C1=1,sol2);
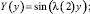
>_EnvAllSolutions:=true:
>solve(sin(lambda(2)*b=0,lambda(2));
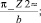
>mu:=m -> pi*m/b;
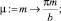
>Y:=(y,m) -> sin(y*mu(m));
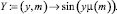
Получаем, что собственным значениям задачи Штурма – Лиувилля (10)–(11)
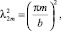m = 1, 2 ... (17)
соответствуют собственные функции вида
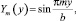m = 1, 2 ... (18)
С учетом равенства (13) найдем
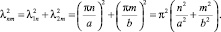(19)
Теперь найдем общее решение уравнения (12), подставляя в него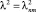 
.
>eq3:=diff(Z(z),z$2)+(k/z)*diff(Z(z),z)-lambda^2*Z(z)=0;
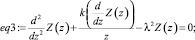
>dsolve(eq3,Z(z));
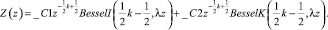
Таким образом, запишем общее решение уравнения (12) в виде
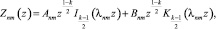(20)
где Anm и Bnm – произвольные постоянные,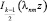 
– функция Бесселя мнимого аргумента 1-го рода, 
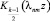– функция Макдональда.
Теперь подставляя (16), (18) и (20) в (7), получим частные решения уравнения (1), удовлетворяющие граничным условиям (4) и (5):
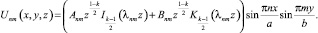(21)
А общее решение будем искать в виде следующего ряда:
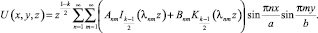(22)
Ряд (22) будет являться решением уравнения (1), удовлетворяющим условиям (4) и (5), если он равномерно сходится и сходятся ряды, полученные из него дифференцированием по переменным x, y, z дважды.
Внесем рассуждения в программу Maple:
>u:=(x,y,z) -> Sum(Sum(Z(z)*X(x,n)*Y(y,m),n=1..infinity),m=1..infinity);
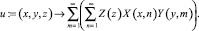
Для нахождения неизвестных коэффициентов Anm и Bnm подставим (22) в граничные условия (6). Сначала вычислим производную, запомнив ее под именем, скажем, «ии», и подставим в нее значение z = 0:
>uu:=(x,y,z) -> diff(u(x,y,z),z);
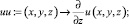
>uu(x,y,0);
В результате программа выдает следующее сообщение об ошибке: «Error, (in BesselK) numeric exception: division by zero». Действительно [1], для выполнения первого условия из (6), нужно положить Bnm = 0. Очевидно, что при Bnm = 0 и 0 < k < 1 условие Uz(x, y, 0) = 0 выполняется. Тогда ряд (22) принимает вид
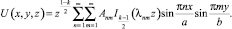(23)
>subs(_C2=0,Z(z));
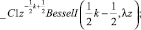
>ZZ:=z -> _C1*z^(-(1/2)*k+1/2)*BesselI((1/2)*k-1/2,lambda*z);
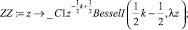
>u:=(x,y,z) -> Sum(Sum(ZZ(z)*X(x,n)*Y(y,m),n=1..infinity),m=1..infinity);
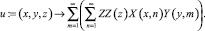
Подставим теперь ряд (23) во второе условие из (6):
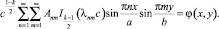
Умножим обе части последнего равенства на выражение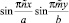 
и проинтегрируем его по переменной х на промежутке от 0 до а, по переменной у на отрезке от 0 до b. При этом будем учитывать равенства [4]:
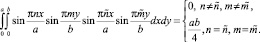
Тогда получим
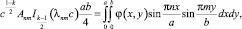
откуда найдем неизвестные коэффициенты:
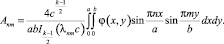(24)
Отметим эти рассуждения в программе и выведем результат.
>u(x,y,c)=phi(x,y):
>assume(n::posint,m::posint);
>subs(_C1=A[n,m], %);
>A[n,m]:=(4*c^((k-1)/2))/(a*b*BesselI((1/2)*k-1/2,lambda*c))*
int(int(phi(x,y)*sin(x*Pi*n/a)*sin(y*Pi*m/b),y=0..b),x=0..a):
>u(x,y,z);
В результате запишем окончательный вид решения краевой задачи (2)-(6):
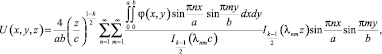(25)
где коэффициенты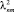 
определяются по формуле (19).
Заключение
С помощью системы компьютерной математики Maple можно решать самые разнообразные задачи. В работе демонстрируется исследование краевой задачи для трехмерного эллиптического уравнения второго порядка с оператором Бесселя, так как программа позволяет использовать методы решения задач, связанных с уравнениями в частных производных, и избежать рутинных математических вычислений в исследовании задач математической физики.