На сегодняшний день существует ряд методов оценки рисков, ставших популярными и традиционными.
Аксиоматический подход к оценке рисков
Рассмотрим конечное вероятностное пространство (Ω, A, P). Обозначим Fx как соответствующую функцию распределения:
x ∈ R → Fx(x) = P(X ≤ x).
Мера риска – это функционал набора случайных доходов от портфельных инвестиций X → p(X) ∈ ¡, она подразумевает возможное соответствие ряду аксиом:
1. Положительная однородность: для каждого случайного дохода от портфельных инвестиций X и реальной ценности λ > 0
ρ(λX) = λρ(Х);
2. Трансляционная инвариантность: для каждого случайного дохода от портфельных инвестиций X и реальной ценности α,
ρ(X + α) = ρ(X) – α;
3. Монотонность: для каждого случайного доход от портфельных инвестиций X и Y, такие, что X ≥ Y,
ρ(X) ≤ ρ(Y);
4. Субаддитивность: для каждого случайного дохода от портфельных инвестиций X и Y,
ρ(X + Y) ≤ ρ(X) + ρ(Y);
5. Инвариантность закона: для каждого случайного дохода от портфельных инвестиций X и Y с функциями распределения Fx и Fy,
Fx = Fy ⇒ ρ(X) = ρ(Y);
6. Аддитивность: для каждых случайных переменных X и Y,
ρ(X + Y) = p(X) + p(Y).
Меры риска, обсуждаемые в работах Арцнера и соавт. [10], соответствуют аксиомам (1)–(4), меры риска искажений в работах Вонга и соавт. [13] соответствуют аксиомам (1, 2, 3, 5, 6), в то время как спектральные меры риска, рассмотренные Ачерби [8], соответствуют всем вышеперечисленным аксиомам.
Эмпирический подход
Рассмотрим множество исторической прибыли на капитал {rl, ..., rn} как реализацию m-мерного строго стационарного процесса, где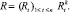 
и обозначает прибыль на капитал k на дату t и каждый 
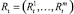показывает прибыль m на дату t. Рассмотрим портфели на основе этой суммы средств, определяемой вектором распределения
a = (a1, ..., am) ∈R m.
При эмпирическом подходе можно положиться лишь на исторические базы данных и не иметь прямого доступа к истинной вероятности PR. Таким образом, вычисленная по историческим данным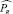 
будет эмпирической мерой.
Пусть случайная переменная X относится к структуре портфеля α, а соответствующая историческая доходность обозначается как {x1,...,xn}. Тогда эмпирическая функция распределения будет выглядеть как
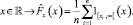
Меры риска, основанные на моменте
Стандартное отклонение Г. Марковица является самым известным, так как оно положило начало стратегиям управления активами в 50-е гг. и до сих пор остается ориентиром в данной области. Эту меру риска можно перенести на более прогрессивные модели. Однако, в дополнение к своему симметричному поведению в отношении доходов и издержек, стандартное отклонение неспособно быть инвариантным и монотонным. По этой причине имеет смысл рассматривать класс односторонних мер риска, основанных на моменте, согласно Фишеру [12]:
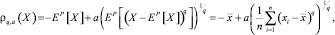
где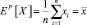 
; Z– = max(–Z, 0); 0 ≤ a ≤ 1; 1 ≤ q ≤ ∞.
q = 1 соответствует одностороннему абсолютному отклонению от среднего значения; оно использовалось в работах Деннеберга [11], а q = 2 связано с нижней полудисперсией.
Деннеберг [11] также рассматривал меры риска на основе абсолютного отклонения от медианы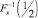 
;
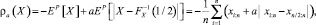
где 0 ≤ a ≤ 1.
Кроме того, Деннеберг показал, что мера риска может быть выведена из квантильной функции как
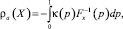
где
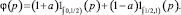
Подход на основе Value-at-Risk
Типичным примером популярной меры риска является Value-at-Risk (или VaR). Value-at-Risk – это конкретный порог, как видно из
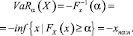
Таким образом, Value at Risk связана с упорядоченной статистикой дохода от портфельных инвестиций. VaR соответствует аксиомам (1, 2, 3, 5 и 6).
Подход на основе ожидаемых потерь
Ожидаемые потери Ачерби и Таше [9] – распространенные примеры когерентной меры риска на основе квантилей дохода. Ожидаемые потери на уровне α можно выразить следующим образом:
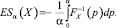
Учитывая, как и ранее, эмпирическую функцию распределения X и поскольку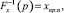 
имеем
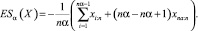
Таким образом, ожидаемые потери – это средневзвешенное значение упорядоченной статистики, которое можно легко вычислить по исторической портфельной доходности. Исходя из предыдущего выражения, легко можно проверить, что α ∈ (0, 1] → ESα(X) – непрерывная и невозрастающая величина. Предельные случаи соответствуют ES1(X) = –EP[X], что является менее пессимистичной мерой риска, и α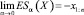 
связана с худшим вариантом.
В отличие от Value-at-Risk, ожидаемые потери являются когерентной мерой риска. Фактически это наименьшая когерентная, аддитивная и инвариантная мера риска, которая доминирует над VaR. Таким образом, ожидаемые потери можно рассматривать как естественное когерентное продолжение Value-at-Risk.
Энтропическая оценка VaR многоуровневого портфеля (EMPVaR)
Традиционные методологии измерения рисков в основном построены на гипотезе эффективного рынка (EMH), которая предполагает структуру однородного рынка с рациональными агентами. Они игнорируют информацию тонкой структуры неоднородного рынка и предоставляют приемлемое приближенное выражение в среднем и долгосрочном временном горизонте. Однако на более коротком временном горизонте происходят некоторые аномалии в эмпирических данных. Потенциальная причина может заключаться в использовании разных временных горизонтов и инвестиционных стратегий инвесторов. К примеру, инвесторы могут решить проводить свои сделки по различным ценам, на бычьем или медвежьем рынке в зависимости от своих предпочтений на коротком, среднем или длинном временном горизонте. Чтобы измерить колебания риска на коротком временном горизонте, должна приниматься во внимание информация о микроструктуре рынка. Последние эмпирические и модельные исследования предлагают значимость структуры неоднородного рынка в пользу Гипотезы неоднородного рынка (НМН), которая предполагает, что рынок состоит из агентов с различными инвестиционными стратегиями и временными горизонтами, а также зависящими от времени взаимоотношениями между различными участниками рынка на разном инвестиционном временном горизонте.
При моделировании на валютном рынке в рамках НМН возникают два теоретических вопроса: во-первых, вопрос моделирования структуры данных, различающихся по характеристикам неоднородных данных, во-вторых, воспрос в отношении критериев определения характеристик средств данных. Таким образом, предлагается энтропическая оценка VaR многоуровневого портфеля (EMPVaR) для решения этих теоретических проблем.
В качестве теоретической базы гипотеза НМН предлагает разрешение эмпирических аномалий, показывая, что в поведении инвесторов можно провести различительную линию при различных инвестиционных временных горизонтах. Таким образом, предположения строятся при формулировании теоретических основ:
1. Инвестиционная деятельность независима в разных временных горизонтах.
2. Инвестиционная деятельность однородна в рамках временных горизонтов.
Поскольку предполагается, что волатильность различна и независима в разных масштабах и однородна в пределах одного масштаба, базисные функции будут проектировать начальный сигнал в более многомерное пространство L2(Rd), определенное как вложенная последовательность L2(Rd) подпространств Vj бесконечная в обе стороны,
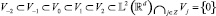и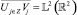 
при
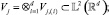
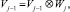
где ⊗ – оператор тензорного произведения.
При случайной переменной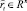 
, полученной с помощью неизвестного процесса получения данных (DGP) c неизвестными параметрами, и наблюдении rt ∈ Rn шенноновская энтропия ошибок определяется как
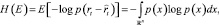
где H(E) относится к шенноновской энтропии ошибок E; p(x) относится к функция плотности вероятности.
Задача состоит в том, чтобы минимизировать Н(Е) путем настраивания различных параметров алгоритма прогнозирования, который производит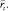 
Матрица дисперсий и ковариаций может быть вычислена из отдельного прогноза матрицы дисперсий и ковариаций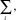 
(i = A, 1, 2, ..., J) в разных масштабах, как в уравнении
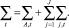
Допустим, что X – это единичные портфельные инвестиции с весом ω и h – дневным сроком владения с прогнозируемым условным средним и матрицами ковариации. Далее следуем традиционному методу дисперсии-ковариации для оценки портфеля VaR,
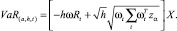
Тем не менее в современных условиях данных подходов недостаточно для оценки риска, потому что они имеют ограниченную природу, то есть не охватывают всех состояний рынка.