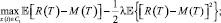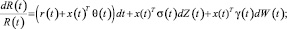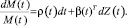В современной рыночной экономике, подверженной кризисам и банкротствам, большое значение приобретает разработка оптимальных стратегий инвестиционного портфеля. В условиях нестабильного рынка при стратегическом инвестировании очень важно уметь создавать безубыточные стратегии. Помимо классических инвестиционных стратегий, которые, как правило, не работают в кризисные периоды, существуют альтернативные стратегии. Часто такие стратегии являются динамическими. В данной статье рассмотрены альтернативные динамические портфельные стратегии.
Оптимизация портфельной стратегии на основе метода Монте-Карло
Опишем модель оптимизации портфельной стратегии на основе метода Монте-Карло. Одну из успешных стратегий предложили авторы Чезари и Кремонини [5]. Они рассматривают модель инвестиционного портфеля для девяти различных состояний рынка, оценивая оптимальную доходность стратегии. Процесс моделирования предназначен для того, чтобы генерировать множество различных сценариев фондового рынка, в которых будет проводиться анализ поведения стратегий портфеля. С точки зрения дохода определяются отрицательные, нулевые и положительные моменты рынка, а с точки зрения риска – периоды волатильности: низкий, средний и высокий. В частности, для доходов авторы определили диапазоны (–30 %; –5 %); (–5 %; +5 %); (+5 %; +30 %), для волатильности рынка – диапазоны (10 %, 15 %); (15 %, 25 %); (25 %, 30 %). Пара доходность - волатильность идентифицирует сценарий рынка, используемый для создания 5-летнего прогностического временного ряда еженедельных доходов от акций. При моделировании методом Монте-Карло с временным интервалом, равным 1 неделе:
1. Из двух равномерных распределений U (–30 %; +30 %) и U (10 %, 30 %) создается вариант прогноза со средней годовой доходностью μ и волатильностью σ;
2. С помощью преобразования Бокса – Мюллера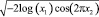 
, где x1; x2 равномерно распределены, U(0, 1), 360 значений данных из нормального распределения N(μ; σ) генерируется случайным образом и первые 100 из них используются для оценки параметра волатильности; Область наблюдения, где n = 100 продлевается, чтобы оценить волатильность. В случае нормальности объективная оценка для σ задается при помощи коррекции обычной оценки: 
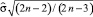. 9 стратегий моделируются за Т = 260 наблюдений (5-летний период) и суммарная статистика подсчитывается с точки зрения производительности и риска.
3. Повторное выполнение производится с шага (1), в общей сложности N = 10 000 вариантов прогноза.
Используются два основных порядка уравновешивания Этциони [6]: временной порядок с еженедельным уравновешиванием (Δt = 1/52) и уравновешивание цены только тогда, когда цены увеличиваются / снижаются на 2,5 % по отношению к предыдущему уравновешиванию. Кроме того, операционные издержки учитываются двумя способами: в виде стоимости пропорциональной значению продаж с = 0,3 % и в качестве поправки к волатильности опциона в соответствии с формулой Леланда [8]:
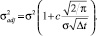
Для того чтобы сравнить эффективность различных стратегий, авторы предлагают использовать набор стартовых портфелей с определенными стратегиями и учитывать их конечную доходность. Для каждого прогноза Чезари и Кремонини [5] рекомендуют рассчитать 8 ежегодных мер рисков и мер доходности:
– Чистую сумму среднего ожидаемого дохода.
– Стандартное отклонение.
– Асимметрию.
– Эксцесс.
– Нижний уровень отклонения.
– Коэффициент Шарпа.
– Коэффициент Сортино.
– Доход, связанный с риском.
Нижний предел отклонения рассчитывается как риск дефицита, то есть риск в результате пороговой доходности ниже нуля.
Нижний предел отклонения:
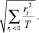
Это особенно полезно в случае асимметрии, и поэтому при анализе эффективности деятельности менеджеров активных портфелей принимается во внимание тот факт, что их целью является изменение распределения дохода по направлению к правой боковой асимметрии.
Таким образом, предлагаемая Чезари и Кремонини оценка портфельных стратегий опирается на предположение, что рынок не имеет кризисных движений и, соответственно, является малоприменимой тогда, когда речь идет о долгосрочном инвестировании. Однако высокую эффективность данная стратегия показывает при краткосрочном инвестировании.
Контрпортфельная оптимизация
Рассмотрим метод оптимизации динамического портфеля, разработанный И. Жао. Модель контрпортфеля подразумевает направленность против рыночных тенденций и активов держателей «идеальных портфелей» [10]. Функционирование данной модели в реальных условиях подразумевает использование более высоких рисков, а также наличие значительного набора резервных финансовых инструментов.
Рассмотрим финансовый рынок, состоящий из m + 1 основных активов: m рисковых активов, S1, …, Sm, и (безрисковых) облигаций, S0. Инвестор может вкладывать средства и в облигации и в рисковые активы. Облигации средствами имеют непрерывно определяемую сложную ставку r(t), которая может быть выражена как
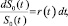(1)
где r(t) является локально безрисковым.
Вероятностное определение рисковых активов имеет следующий вид: n – независимое броуновское движение; Z1(t), …, Zn(t) характеризуют рыночную нестабильность для всех рисковых активов. Эти коэффициенты являются ненаблюдаемыми. Нестабильность частично проявляется в стоимости активов. Кроме того, все рисковые активы имеют свои собственные компоненты риска, управляемые независимым броуновским движением W1(t), …, Wm(t). Zi и Wi определены на фильтрованном вероятностном пространстве (Ω, {Ft}, F, P), где Ft – это расширение естественной фильтрации.
С учетом вышеизложенного предположим, что броуновское движение n + m генерирует стоимость m рисковых активов. В частности, предположим, что стоимость рисковых активов определяется диффузным процессом со многими переменными:
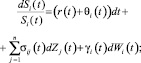
для i = 1, …, m, (2)
где θi(t) – мгновенная рисковая премия актива i; σij(t) – мгновенная волатильность актива i при изменении коэффициента риска Zj(t); γi(t) – диверсифицируемый риск Si.
С целью облегчения вычислений эти параметры должны изменяться как можно чаще. Уравнения (1) и (2) совместимы с моделями определения стоимости активов в непрерывном времени. Вышеуказанные модели определения стоимости активов позволяют построить эффективные модели систематического и диверсифицируемого риска, такие как модель арбитражного ценообразования Росса [9] в дискретном времени.
Пусть xi(t) – доля накоплений инвестора, вложенных в рисковый актив i во время t для i = 1, ..., m, с остатком, равным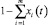 
, вложенным в облигации. Предположим, что x1(t), …, xm(t) допустимы и Ft представляет собой применяемый процесс контроля, то есть xi(t) является неупреждающей функцией, соответствующей условию ограниченного изменения
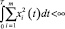
для инвестиционного горизонта T < ∞.
Рассмотрим валовую доходность, равную стоимости инвестиционного портфеля, разделенной на первоначальную стоимость портфеля в любой момент времени.
Пусть R(t) – валовая доходность портфеля во время t. Доходность портфеля определяется по формуле
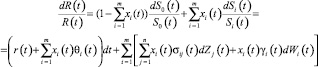(3)
при начальном значении R(0) = 1. Для лучшего истолкования примем матричное представление:
σ(t) = [σij(t)]; θ(t) = [θ1(t), …, θm(t)]T;
γ(t) = diag[γ1(t), …, γm(t)]; x(t) = [x1(t), …, xm(t)]T;
Z(t) = [Z1(t), …, Zn(t)]T; W(t) = [W1(t), …, Wm(t)]T,
где σ(t) –матрица m×n; γ(t) – диагональная матрица размера m×m; θ(t) и x(t) – m-мерные векторы-столбцы; Z(t) и W(t) – n-мерное и m-мерное броуновское движение соответственно.
Таким образом, уравнение (3) может быть переписано как
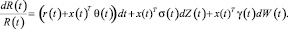
Для исключения остальных активов предположим, что [σγ] – полный строчный ранг, то есть σσT + γγT является обратимой матрицей. При выборе допустимых портфелей не существует других ограничений, таких как: продажи без покрытия, непрерывный трейдинг и транзакционные издержки. Для стохастической интегрируемости необходимо соблюдать следующие условия в отношении допустимости портфельной политики x(t):
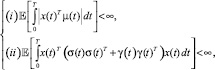(4)
где Ε – оператор математического ожидания.
Пусть CT – множество всех m-мерных стохастических процессов в соответствии с условиями формулы (4), а условие конечной дисперсии может быть записано как
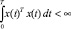
для некоторых T < ∞.
Таким образом, CT состоит из допустимых портфелей. Рассмотрим эталонный портфель и его оптимальную эффективность.
Пусть валовая доходность эталонного портфеля определяется стохастическим процессом:
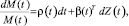
где ρ(t) и β(t) – мгновенная ставка доходности и вектор волатильности.
Это определение соответствует модели Росса [9] и сочетается с существующими линейными моделями определения стоимости активов. Основное отличие этой модели от существующих моделей определения стоимости активов заключается в том, что она не основывается на множестве заранее заданных факторов, которые необходимы для определения стоимости всех активов в экономическом обращении. Возвращаясь к динамике финансовых инструментов, можно сказать, что каждый из них по отдельности в дополнение к своему «инструментальному» специфическому риску (броуновское движение W(t)) имеет компонент риска, зависящий от тех же факторов (броуновское движение Z(t)). Ферсон и др. [7] провели общее тестирование моделей со скрытыми переменными. Они отметили, что «модели со скрытыми переменными допускают изменение ожидаемой доходности во времени в виде функции небольшого количества рисковых премий, обычно присущих активам». Аналогично их модели данная модель не допускает функциональной формы условной ожидаемой доходности и, таким оборазом, избегает получения искаженных выводов из неопределенной модели.
Известно, что максимизация ожидаемой логарифмической полезности накоплений эквивалентна максимизации геометрического темпа роста. Вектор весов портфеля оптимального роста определяется как
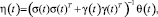
где η(t), γ(t), θ(t) и r(t) – общие стохастические процессы с незначительными ограничениями по отношению к стохастической интегрируемости.
Оптимальный портфель может быть подсчитан на основе двух частей. Первая часть – это оптимум роста, а вторая часть – компонента хеджирования потенциальных возможностей стохастического инвестирования. Пусть G(t) – доходность портфеля оптимального роста во время t, тогда динамика G(t) может быть выражена как
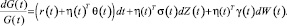
Оптимальный ожидаемый темп роста, определяемый как средняя величина функции оптимального значения в инвестиционном горизонте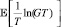
, равен
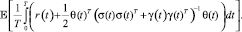
Если σ(t), γ(t), θ(t) и r(t) являются постоянными во времени, оптимальный темп роста составляет
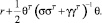
В долгосрочной перспективе оптимальный рост может быть достигнут любым портфелем с вероятностью 1. Это является мотивацией для инвестирования в портфель оптимального роста при долгосрочном инвестиционном горизонте.
Используем λ как чувствительность к риску, тогда оптимальная модель портфеля инвестора может быть сформулирована как
