Теоретико-игровые модели могут быть успешно использованы для решения проблем согласования разнонаправленных интересов сторон таможенного обслуживания, так же как ранее в применении к ставшим достаточно традиционными проблемам организации и ко всему многообразию экономической проблематики [1, 3, 5]. В бескоалиционной теории игр основной единицей анализа является индивидуальный участник, который старается обеспечить получение максимального эффекта с учетом действия определенных правил и ограничений [4].
В качестве единиц анализа примем участника внешнеэкономической деятельности и таможенного представителя, имеющего наибольшее значение в подсистеме услуг в таможенной сфере. Рассмотрим биматричную игру, в которой каждый игрок имеет две стратегии, условно обозначаемые терминами «обмануть» и «сотрудничать».
Пусть игрок А, таможенный представитель, реализует две стратегии:
А1 – использовать простейшие формы декларирования («обмануть клиента»);
А2 – использовать наиболее выгодные для клиента формы декларирования («сотрудничать»).
Подобное деление основано на слабой заинтересованности таможенного представителя в применении современных форм и методов осуществления таможенного оформления и прохождения таможенного контроля. Пользуясь низкой квалификацией клиента в вопросах организации таможенного оформления, таможенный представитель использует шаблонные декларации, затрачивая на оформление каждой из них минимальное время, не предлагая заказчику более сложных в реализации возможностей применения современного таможенного инструментария – предварительного декларирования, подачи периодической декларации, использования технологии удаленного выпуска.
В свою очередь игрок В, клиент, реализует две стратегии:
В1 – продолжать проводить таможенное оформление с помощью того же таможенного представителя («сотрудничать»);
В2 – уйти от таможенного представителя и заполнять декларацию своими силами («обмануть»).
Введем следующие обозначения. Параметры, входящие в матрицу A:
i – доход от оформления единицы поставки заполнением одной простой декларации;
I – доход от оформления единицы поставки с помощью одного из видов сложного декларирования;
n – количество оформленных простых деклараций;
–t – упущенная выгода, определяемая отсутствием запаса времени между обращениями клиента при постоянном заполнении простых деклараций;
T – выгода, следующая из запаса времени между обращениями клиента, высвобождающегося у таможенного представителя при использовании одного из видов сложного декларирования;
s – упущенная выгода.
При использовании простых деклараций таможенный представитель получает сравнительно небольшой доход с каждой декларации, что компенсируется в случае больших объемов обслуживаемого внешнеторгового оборота и частых поставках при незначительных трудовых затратах исполнителя. Тогда постоянное использование только простых технологий превращает таможенного представителя в исполнителя механических функций, что ведет к потере времени на выполнение шаблонных операций (и не позволяет ему получить необходимый опыт применения современных форм таможенного оформления) и недополучению потенциально более высокой прибыли (–t).
В свою очередь, постоянный поиск новых возможностей сокращения временных и финансовых издержек для клиента путем применения современного таможенного инструментария ведет к росту профессионального уровня таможенного представителя, повышая его привлекательность и востребованность на рынке услуг в таможенной сфере, что в предложенной модели выражено параметром T.
Необходимо также учитывать упущенную выгоду (s), возникающую из-за неоправданных усилий таможенного представителя в случаях, когда, несмотря на применение исполнителем всех возможностей декларирования, клиент уходит.
Для построения матрицы выигрышей таможенного представителя рассмотрим различные комбинации возможных ходов сторон (табл. 1).
Таблица 1
Матрица выигрышей таможенного представителя
|
Игрок A |
B1 |
B2 |
|
A1 |
a11 = in – t |
a12 = i |
|
A2 |
a21 = I + T |
a22 = –T + I – s |
Комбинация А1В1 – таможенный представитель оформляет только простые декларации, а клиент пользуется его услугами на протяжении достаточно длительного времени. При повторяющихся импортных поставках таможенный представитель подает оформляемые по единому шаблону декларации, не затрачивая на их заполнение значительных усилий. Игрок А получает стандартный доход от заполнения простой декларации, умноженный на количество деклараций, но затрачивает время на выполнение механических операций и недополучает возможную прибыль, в результате его выигрыш составляет a11 = in – t.
Комбинация А1В2 – таможенный представитель оформляет только простые декларации, а клиент уходит, рассчитывая в дальнейшем на самостоятельное оформление декларации. Уход клиента может быть обусловлен как снижением рентабельности внешнеэкономической деятельности, так и потерей доверия к посреднику и желанием самостоятельно оформлять декларации по шаблону. Таможенный представитель получает стандартный доход от заполнения простой декларации, но клиент больше не возвращается, в результате выигрыш игрока А составляет a12 = i.
Комбинация А2В1 – таможенный представитель применяет различные виды сложного декларирования, а клиент продолжает пользоваться его услугами. Игрок А получает доход от применения сложных форм декларирования, больший, чем при заполнении простой декларации, и запас времени Т. Выигрыш игрока А составляет a21 = I + T. Запас времени может образовываться в результате применения периодического декларирования, а также при использовании предварительного декларирования. В результате таможенный представитель может получить больший доход за оформление отдельной декларации, а полученное время потратить на оформление простых деклараций для того же или другого клиента.
Комбинация А2В2 – таможенный представитель применяет различные виды сложного декларирования, а клиент уходит, рассчитывая в дальнейшем на самостоятельное оформление деклараций. Игрок А получает увеличенный доход от заполнения сложной декларации, но клиент уходит, поэтому время, затраченное на сложное декларирование, можно считать потраченным неэффективно, так как таможенный представитель в это время упустил выгоду, отказался от других вариантов, и его выигрыш составляет a22 = –T + I – s.
Построим аналогичную матрицу выигрышей для клиента с параметрами:
–p – расходы по оплате услуг таможенного представителя при заполнении простой декларации;
n – количество оформленных простых деклараций;
–P – расходы по оплате услуг таможенного представителя при применении одного из видов сложного декларирования;
U – выгода клиента при уходе от таможенного представителя в том случае, если клиент будет самостоятельно заполнять простые декларации;
u – выгода клиента при уходе от таможенного представителя в том случае, если клиент будет самостоятельно использовать сложные виды декларирования;
W – выгода, появляющаяся у клиента, если таможенный представитель применяет один из видов сложного декларирования и клиент продолжает сотрудничество.
Параметры –p и – P характеризуют расходы клиента и определяются стоимостью услуг таможенного представителя, при этом применение в ходе оформления сложных методов декларирования ведет к увеличению стоимости обслуживания.
Матрица выигрышей клиента при различных комбинациях стратегий игроков А и В представлена в табл. 2.
Таблица 2
Матрица выигрышей клиента
|
Игрок B |
B1 |
B2 |
|
A1 |
b11 = –pn |
b12 = U – p |
|
A2 |
b21 = W – P |
b22 = u – P |
Комбинация А1В1 – таможенный представитель оформляет только простые декларации, а клиент пользуется его услугами на протяжении достаточно длительного времени. Игрок В оплачивает стандартные услуги посредника многократно, и выигрыш В составляет b11 = –pn. При больших объемах внешнеторгового оборота и значительном количестве поставляемых партий затраты участника ВЭД на оплату услуг таможенного представителя могут быть очень велики. При ограниченной номенклатуре оформляемых грузов такие высокие затраты, низкая сложность заполнения декларации и отсутствие заметных изменений в ее содержании может побудить клиента отказаться от услуг таможенного представителя и продолжить декларирование самостоятельно.
Комбинация А1В2 – таможенный представитель оформляет только простые декларации, а клиент уходит, рассчитывая в дальнейшем на самостоятельное оформление декларации. Игрок В оплачивает услуги посредника и в случае ухода имеет возможность получить выгоду при самостоятельном заполнении декларации. При типовых поставках неизменной номенклатуры грузов оформление деклараций по шаблону, полученному у таможенного представителя, является несложной задачей, для выполнения которой может быть достаточно одного специалиста по таможенному оформлению, введенного в структуру компании-участника ВЭД. В результате выбора такой стратегии в рассматриваемой модели выигрыш игрока В может быть обозначен как b12 = U – p.
Комбинация А2В1 – таможенный представитель применяет различные виды сложного декларирования, а клиент продолжает пользоваться его услугами. Игрок В оплачивает услуги по заполнению сложной декларации и получает выгоду, выраженную в максимальном сокращении временных и финансовых затрат по таможенному сопровождению ВЭД. При этом постоянное сотрудничество с одним и тем же представителем позволяет клиенту получать максимально эффективное обслуживание, в том числе и при изменяющихся условиях поставки. Выигрыш игрока В в случае продолжения сотрудничества составляет b21 = W – P.
Комбинация А2В2 – таможенный представитель применяет различные виды сложного декларирования, а клиент уходит, рассчитывая в дальнейшем на самостоятельное оформление декларации. Игрок В оплачивает услуги представителя по использованию сложного декларирования, и, поскольку он уходит, то возможно получение выгоды и при самостоятельном применении современных методов таможенного оформления. В этом случае выигрыш игрока В составляет b22 = u – P.
Различия выигрышей в зависимости от комбинаций стратегий ставят задачу поиска для каждого из игроков стратегий, приносящих наибольший выигрыш или минимально возможный проигрыш. Проведем расчет возможных выигрышей сторон на основе платежных матриц из табл. 1, 2, при этом все рассматриваемые переменные положительны, кроме того n > 1, U > u, T > t, I > i, P > p.
Все разнообразие стратегий в зависимости от выигрыша представим в табл. 3.
Таблица 3
Возможные выигрыши сторон
|
min min |
max min |
min max |
max max |
|
|
Для игрока А |
–T + I – s |
i |
I + T |
In – t |
|
Для игрока В |
–pn |
u – P |
U – p |
W – P |
Если бы данная игра выполнялась один раз, оптимальным выбором игроков были бы осторожные стратегии, однако при повторении игры положение меняется.
Действительно, допустим, что игрок А выбирает стратегию А1 и придерживается ее до тех пор, пока игрок В продолжает пользоваться его услугами. В этом случае формируется сочетание А1В1, при котором продолжительное сотрудничество с одним и тем же клиентом обеспечивает максимальный выигрыш таможенного представителя, а выигрыш клиента оказывается минимальным.
Высокие затраты по таможенному оформлению могут привести к тому, что клиент решит отказаться от услуг таможенного представителя, решив проводить оформление своими силами, что приведет к возникновению сочетания А1В2. Оно соответствует ситуации, при которой таможенный представитель все время заполняет простые декларации, а клиент уходит. Клиент может без значительных усилий перейти на самостоятельное заполнение простых деклараций, экономя средства на услугах посредника. Тогда уже после нескольких таких ходов А поймет это и решит отклониться от данного состояния, выбрав стратегию А2, поскольку единоличное отклонение позволит ему увеличить свой выигрыш при заполнении сложной декларации, что увеличит разовый доход. При этом сложится ситуация А2В2, в которой выигрыш таможенного представителя является минимальным, поэтому переход на стратегию А2 будет применяться посредником только вынужденно – либо по прямому требованию клиента, либо в результате заметного сокращения спроса на услуги по оформлению простых деклараций.
Результатом применения современных методов декларирования станет сокращение совокупных издержек участника ВЭД и повышение эффективности его работы. Клиент, поняв, что его не обманывают, а обслуживают с помощью современных инструментов, принимает решение остаться, так как уходить и самостоятельно проводить таможенное оформление окажется для него значительно более сложной задачей, чем в случае копирования простой декларации. Таким образом, сложится ситуация А2В1.
Однако при отсутствии должной мотивации и контроля со стороны заказчика игрок А с большой вероятностью примет решение сократить собственные затраты и вновь перейти на заполнение простых деклараций, что при низком уровне квалификации клиента останется незамеченным. В результате сложится ситуация А1В1, соответствующая начальному положению.
Таким образом, при многократном повторении игры игроки могут чередовать стратегии, используя не какую-то одну, «чистую» стратегию, а «смешанные» стратегии, сочетающие в себе «чистые» стратегии с определенной частотой [2, c. 46]. Тогда задача сводится к поиску не просто оптимальных стратегий, дающих максимальный выигрыш, а тех, которые обеспечивают его при многократном повторении игры. Согласно теореме Нэша, поиск следует осуществлять среди состояний, при которых единоличное отклонение любого из игроков от выбранной стратегии не увеличивает его выигрыш, когда другие своих стратегий не меняют (у игроков отсутствует стимул к отклонению). Равновесие Нэша в смешанных стратегиях существует в каждой конечной игре и достигается нахождением пар таких стратегий (x*, y*), для которых выполняются условия
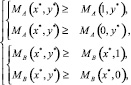(1)
где x* – частота применения игроком А стратегии А1 в равновесном состоянии (0 ≤ x* ≤ 1); y* – частота применения игроком В стратегии В1 в равновесном состоянии (0 ≤ y* ≤ 1); – математическое ожидание выигрыша (оптимальный средний выигрыш) игрока А при использовании игроком А стратегии А1 с частотой x* и игроком В стратегии В1 с частотой y*; MB(x*, y*) – математическое ожидание выигрыша (оптимальный средний выигрыш) игрока В при использовании игроком А стратегии А1 с частотой x* и игроком В – стратегии В1 с частотой y*; MA(1, y*) и MA(0, y*) – математическое ожидание выигрыша (оптимальный средний выигрыш) игрока А стратегии А1 с частотой 1 и 0 соответственно, а игроком В – стратегии В1 с частотой y*; MB(x*, 1) и MB(x*, 0) – математическое ожидание выигрыша (оптимальный средний выигрыш) игрока В при использовании игроком А стратегии А1 с частотой x*, а игроком В – стратегии В1 с частотой 1 и 0 соответственно.
В результате поиска решений приведенных систем неравенств путем подстановки имеющихся значений выигрышей получим множество решений. Для подсистемы (1) оно состоит:
1) из всех ситуаций вида (0, y*),
где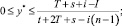 
2) всех ситуаций вида
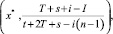
где 0 < x* < 1;
3) всех ситуаций вида (1, y*),
где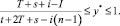 
Множество решений подсистемы (2) состоит:
1) из всех ситуаций вида (x*, 0),
где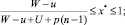 
2) всех ситуаций вида
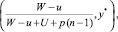
где 0 < y* < 1;
3) всех ситуаций вида (x*, 1),
где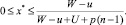 
Решением игры является вектор (x*, y*), составленный из x*, y*, общих для рассмотренных выше множеств. Изображение множеств в виде графиков (рис. 1, для подсистемы (1) – жирная линия, для подсистемы (2) – пунктирная линия) показывает, что имеется одна общая точка С, результат пересечения ломаных, равновесие Нэша в исследуемой игре.
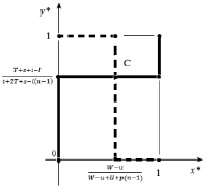
Рис. 1. Графическое представление решения игры
Таким образом, при многократном повторении игры:
– для игрока А оптимальным является применение стратегии А1 (выполнять простые формы декларирования) с частотой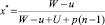 
и применение стратегии А2 (применять сложные формы декларирования) с частотой 
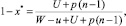средний выигрыш составит
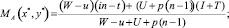
– для игрока B оптимальным является применение стратегии B1 (остаться) с частотой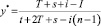 
и применение стратегии B2 (уйти) с частотой 
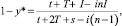средний выигрыш составит
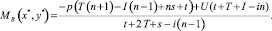
Легко проверить, что равновесные выигрыши игроков А и В превышают их выигрыши при максиминных стратегиях.
На основе формул для x* и y* при определенных значениях параметров получаются оптимальные значения частот применения той или иной стратегии первого и второго игроков. Анализируя оптимальную стратегию таможенного представителя, которая определяется частотой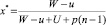 
выполнения простых форм декларирования, видим, что чем выше стоимость простого декларирования для клиента, тем целесообразнее переходить на сложные формы декларирования, выше вероятность того, что клиент охотнее пойдет на него и не расстанется с таможенным представителем. Чем выше выгода от самостоятельного выполнения клиентом простых форм декларирования, тем более следует уходить от простых форм, поскольку тогда в случае сложного декларирования меньше вероятность ухода клиента.
Чем больше разница между выгодой от сложных форм декларирования, выполненных таможенным представителем, и самостоятельным выполнением сложных форм, тем чаще можно применять и простые формы декларирования (рис. 2), риск потерять клиента меньше, поскольку опыт сотрудничества на основе сложных форм говорит клиенту о большей выгоде сотрудничества с таможенным представителем.
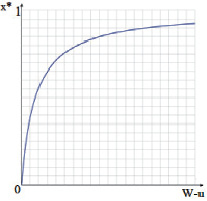
Рис. 2. График функции x*(W – u)
Таким образом, постоянно заполняя простые декларации, таможенный представитель может получить максимальный доход при условии, что клиент будет продолжать с ним сотрудничать. При наличии высокого спроса на услуги по таможенному оформлению таможенному представителю выгодно использовать простые формы декларирования, обеспечивающие ему максимальный доход. При этом для клиентов оформление большого числа простых деклараций зачастую будет экономически неэффективным. Следствием такой стратегии таможенного представителя становится постепенная потеря клиентов, в результате которой доход, получаемый при оформлении небольшого числа простых деклараций, оказывается меньше потенциального дохода, получаемого при заполнении сложной декларации. Однако применение сложных форм декларирования может быть невыгодным для таможенного представителя, если вероятность ухода клиента велика, поэтому оптимальной будет смешанная стратегия.