Рассмотрим задачу формирования инвестиционной стратегии интегрированной иерархической производственной структуры, примером которой является вертикально-интегрированный холдинг. В его структуре выделяются однородные группы «стратегических бизнес-единиц» (СБЕ), характеризующиеся примерно одинаковым уровнем риска в производственной и финансовой сферах деятельности [3, 5].
Каждая СБЕ формирует собственную инвестиционную стратегию, направленную на снижение внешнего и внутреннего риска. Для реализации этой стратегии, включающей набор прошедших согласование инвестиционных проектов (ИП) отдельных СБЕ, предполагается выделение материальных и финансовых ресурсов, которые включают собственные и заемные средства СБЕ, а также средства централизованного инвестиционного фонда холдинга, которыми распоряжается исполнительный центр (управляющая компания – УК).
При такой постановке задачи оценки инвестиционных возможностей холдинга и выбора оптимального по рыночному критерию набора инвестиционных программ СБЕ возможная формализация методологии СВА «затраты - эффект» связывается с экономико-математическим моделированием процедуры отбора эффективных инвестиционных проектов с учетом их принадлежности к определенной группе риска [2].
Возможность балльной оценки результатов реализации технических проектов СБЕ с учетом снижения рыночного и производственного риска является основой формализации. Оценка затрат на реализацию инвестиционных проектов СБЕ может быть основана на внутренних (трансфертных) ценах и нормативах объективно необходимых затрат инвестиционных ресурсов, определяемых на уровне управляющей компании. Трансфертные цены не включают составляющих рыночных транзакций и определяются в рамках используемой предприятиями холдинга системы управленческого учета.
Введем обозначения:
i = 1, ..., Iq – индекс СБЕ в q-й группе (q = 0, 1, 2, 3), где q = 0 – риск рыночной деятельности отсутствует; q = 1 – приемлемый уровень риска; q = 2 – критический уровень риска; q = 3 – катастрофический уровень риска.
ri = 1, ..., Ri – индекс ИП i-й СБЕ в выбранной нумерации проектов (например, лексикографической);
j = 1, ..., J – индекс сферы рыночной деятельности, характеризуемой методом оценки результатов, затрат и риска;
bj – балльная оценка планируемого снижения риска подразделений холдинга в j-й сфере;
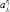– балльная оценка планируемого снижения риска в j-й сфере при реализации ri-го ИП i-й СБЕ;
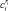– затраты денежных (включающие единовременные капитальные вложения в УК, а также приведенные к началу реализации проекта текущие затраты, дисконтированные по внутренней ставке дисконта) и приведенных к денежному эквиваленту инвестиционных средств УК, которые предполагается выделить на ri-й ИП. Приведение к денежному эквиваленту осуществляется на основе трансфертных цен.
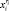– булева переменная, характеризующая принятие или отклонение ri-го проекта i-й СБЕ.
Дискретная модель формирования оптимальной стратегии инвестирования q-й группы СБЕ может быть представлена следующим образом:
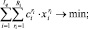(1)
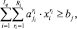j = 1, ..., J; (2)
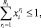i = 1, ..., Iq; (3)
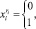i = 1, ..., Iq, ri = 1, ..., Ri. (4)
Решение задачи (1)–(4) основано на поиске решения соответствующей непрерывной модели. В данной задаче ограничения (4) заменяем на ограничения неотрицательности переменных:
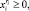i = 1, ..., Iq, ri = 1, ..., Ri. (4′)
Двойственная задача (5)–(7) соответствует прямой задаче линейного программирования (1)–(4′):
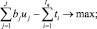(5)
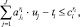i = 1, ..., Iq, ri = 1, ..., Ri; (6)
uj ≥ 0, ti ≥ 0, j = 1, ..., J, i = 1, ..., Iq. (7)
В записи задач (5)–(7) uj является двойственной оценкой ограничения вида (2), на который необходимо снизить риск j-й сферы деятельности q-й группы СБЕ; ti – двойственная оценка i-го ограничения вида (3), т.е. двойственная оценка i-й СБЕ.
Рассматривая в дальнейшем процедуру нахождения оптимального решения задачи (1)–(4), обозначим индексом k переменные, которые относятся к k-му шагу. На шаге k получены решения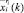 
и uj(k) пары сопряженных задач (1)–(4′) и (5)–(7), позволяющие определить вектор 
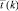двойственных оценок [4]:
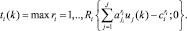(8)
Такой метод определения оценок ti(k) обусловлен необходимостью в удовлетворении соотношениям, которые вытекают из второй теоремы двойственности. Отметим, что экономическая интерпретация соотношения (8) очевидна: на k-м шаге оценка i-й СБЕ определяется как максимальная из оценок возможных вариантов организации инвестиционной деятельности. Если эффективные ИП отсутствуют (совокупная оценка которых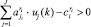 
), то двойственная оценка СБЕ равна нулю (соответствует условию 
).
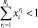В данном случае под эффективными ИП понимаются те, для которых величина балльной оценки эффекта от снижения риска во всех сферах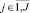 
«не ниже» запланированных затрат.
Установим целочисленный план шага k:
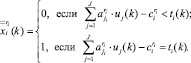(9)
В соответствии с соотношением (9) осуществляется отбор эффективных ИП, при этом для некоторых СБЕ их может быть более одного. Данные проекты образуют множество решений k-го шага и заносятся в список эффективных проектов СБЕ q-й группы.
Для того чтобы перейти к следующему шагу, нужно внести корректировки в задачи (1)–(4) и (5)–(7), связанные с уточнением полученного на k-м шаге списка эффективных ИП: следует сформировать новые списки СБЕ и проектов, исключив из них пары (i, ri), для которых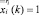 
. Одновременно необходимо внести корректировки в правые части ограничений (2):
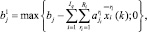(10)
где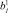 
– скорректированное значение балльной оценки риска j-й сферы q-й группы СБЕ, которое следует использовать на шаге k + 1.
В остальном структура и наполнение моделей (1)–(4) и (5)–(7) остаются прежними.
Итерационная процедура является конечной, обеспечивающей единственность оптимального целочисленного решения. Действительно, конечность гарантируется наступлением одного из 3-х событий: или список пар (i, ri) исчерпывается, или на очередном шаге для всех выполняется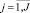 
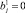(это соответствует случаю, когда все стратегические цели инвестиционной политики, поставленные УК, исчерпаны), или целочисленные планы на двух соседних итерациях совпадают.
Можно предложить следующий способ «повышения скорости» поиска оптимального решения рассматриваемой дискретной модели. Этот способ основан на коррекции двойственных оценок ограничений (2).
А именно, введем в рассмотрение корректор τj(k + 1) j-го ограничения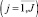 
для шага k 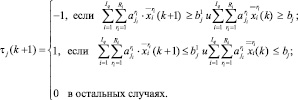+ 1:
(11)
Корректор τj(k + 1) демонстрирует направление, в котором необходимо сдвинуть на очередной итерации оценку uj. В случае устойчивого «перевыполнения» плана по сокращению уровня риска j-й сферы q-й группы СБЕ, на очередной итерации следует уменьшить оценку uj. В случае устойчивого «недовыполнения» плана – ее следует увеличить. В неопределенных случаях следует оставить той же.
Сдвиг оценки uj осуществляется по правилу:
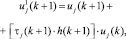(12)
где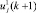 
– скорректированная оценка j-го ограничения типа (2), которую следует применить на шаге k + 1;
h(k + 1) – величина сдвига. В предлагаемом методе в качестве элементов последовательности h(k) используются члены гармонического монотонного ряда:
h(k) → 0;
h(k + 1) < h(k); (13)
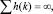
что обеспечивает нивелирование эффекта коррекции с ростом шага итерации и одновременно близость значений коррекции для соседних итераций.
Единственность решения задачи (1)–(4) в случае, если оптимальный план непрерывной задачи (5)–(7) является невырожденным, гарантируется корректностью процедуры формирования вектора двойственных оценок СБЕ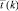 
и однозначностью применения правила (9).
Качество полученного целочисленного плана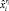 
может быть оценено близостью функционалов (1) непрерывной и дискретной задач:
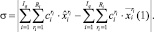(14)
Целочисленный план включает список пар (i, ri) СБЕ и проектов (i = 1, ..., Iq; ri = 1, ..., Ri), который рекомендуется использовать при формировании инвестиционной стратегии q-й группы СБЕ.
Объем Sq централизованного финансирования определяется значением функционала (1):
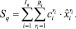(15)
В случае дефицита средств централизованного фонда: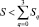 
необходимо повысить требования к качеству инвестиционных стратегий или сразу для всех СБЕ, или целенаправленно для конкретной группы. Последнее достигается изменением вектора правых частей ограничений (2): следует увеличить балльную оценку требуемого уровня результата реализации инвестиционных стратегий в наиболее значимых с точки зрения планирующего органа сферах, характеризующих совокупный риск рассматриваемой группы СБЕ. В последнем случае у УК сохраняется возможность и прямого директивного изменения сформированного списка (i, Ri).
Предположим следующий вариант модели с критерием на максимум и ограничением на объем средств УК, выделяемом на финансирование проектов q-й группы СБЕ.
Выделим множество индексов сфер, характеризующих совокупный риск q-й группы СБЕ, для которых сохраняются ограничения вида (2) (в этих сферах необходимо повысить значение балльной оценки на планируемую величину bj), в отдельный класс J1. Множество остальных индексов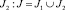 
. Объем выделенного централизованного финансирования ИП q-й группы СБЕ обозначим Sq.
Сохраняя введенные выше обозначения, сформулируем оптимизационную задачу формирования перечня ИП СБЕ q-й группы при заданном ограничении на общий объем финансирования из централизованного инвестиционного фонда:
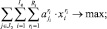(16)
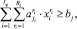j ∈ J1; (2′)
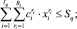(17)
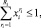i = 1, ..., Iq; (3)
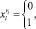i = 1, ..., Iq, ri = 1, ..., Ri. (4)
Метод решения задачи (16), (2′), (17), (3), (4) идентичен методу решения задачи (1)–(4).
Составим двойственную задачу к непрерывной задаче (16), (2′), (17), (3), (4′):
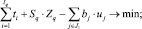(18)
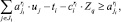
j ∈ J2, i = 1, ..., Iq, ri = 1, ..., Ri; (19)
uj ≥ 0, ti ≥ 0, tq ≥ 0, j ∈ J1,
i = 1, ..., Iq, q = 0, 1, 2, 3.. (20)
В задаче (18)–(20) переменные uj и ti имеют аналогичное содержание, как и в задаче (5)–(7). Добавленная переменная Zq является двойственной оценкой ограничения (17), а именно оценкой средств УК, направляемых на финансирование ИП q-й группы СБЕ.
Для этой задачи вектор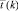 
двойственных оценок для шага k будет задаваться следующими соотношениями:
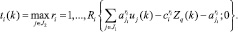(8′)
Соотношения (1)–(4) переносятся на вновь рассматриваемую модель.
Отметим, что наличие в записи модели разнонаправленных ограничений (2′) и (17) является ее существенной особенностью. А именно, для некоторой группы q выделенного финансирования Sq может оказаться недостаточно, и тогда задача не будет иметь решения.
Предложенный численный алгоритм решения двухуровневой целочисленной задачи оптимизации финансирования инвестиционных стратегий групп СБЕ, образующих организационную структуру холдинга, аналогичен алгоритму, который применен в методе Данцинга – Вулфа и основан на взаимном обмене информацией (все показатели эффективности ИП передаются УК отдельным СБЕ, а в обратном порядке направляются сверхэффективные инвестиционные стратегии СБЕ). В нашем случае оценками эффективности ИП СБЕ являются «дискретные оценки», которые позволяют на первом шаге получить приближенное к оптимуму решение дискретной задачи верхнего уровня. В данном случае нет необходимости заранее иметь все возможные ИП нижестоящих СБЕ. Более того, эти проекты можно вводить в модель отдельными группами на следующей итерации, что существенно сказывается на размерности дискретной задачи, которая является ее «узким» местом [1].