На современном этапе модернизации предприятий агропромышленного комплекса (АПК), работающих в условиях возросших экономических рисков и неопределённости, важным вопросом является применение математических методов прогнозирования для достоверной оценки уровня экономической деятельности предприятий в будущем и оптимального управления его функционирования в текущей ситуации. Для решения этой проблемы необходим анализ ключевых экономических показателей организации, формирование модели долгосрочного прогноза финансово-экономической деятельности и дальнейшего развития.
В качестве признаков надвигающегося банкротства предприятия можно рассматривать устойчивое ухудшение текущей финансово-хозяйственной деятельности организации а также резкие изменения в структуре баланса и отчета о прибылях и убытках. Чтобы избежать такого положения, необходимо исследовать факторы, влияющие на доходность организации, и выполнить вычислительные процедуры для получения достоверного экономического прогноза на долговременный период. Для оценки темпов экономического роста целесообразно проанализировать результаты финансово-хозяйственной деятельности и уровень чистой прибыли предприятия. Динамика этого показателя свидетельствует о наличии у предприятия источника формирования и пополнения оборотных средств [2].
Исходными экономическими показателями предприятия для исследования являются данные, собранные за определенный период, который формируется из равных временных интервалов. Результатом статистической обработки данных является функция, отражающая текущее финансово-экономическое положение предприятия. Её параметрический анализ даёт возможность построения долговременного прогноза на будущий период хозяйственной деятельности предприятия. При этом необходим учёт внешних факторов финансовой политики организации, дающий возможность руководителю повлиять на количественные и качественные экономические показатели предприятия, выбрав наиболее перспективные пути развития [3].
Комплексный анализ математических методов, позволяющих разработать модель управления финансово-экономической деятельностью производственного предприятия АПК, показал, что наиболее приемлемым для решения поставленной задачи является метод Е.В. Воскресенского [1]. Рассмотрим алгоритмическую форму этого метода для экономических показателей учебно-производственного предприятия АПК (рис. 2). Для оценки темпов роста анализируется чистая прибыль организации на пятилетнем интервале времени. Данный экономический показатель является ключевым, т.к. свидетельствует о наличии у предприятия источника пополнения оборотных средств, причем искомая функция, характеризующая динамику доходности выбранного предприятия, неизвестна.
В соответствии с алгоритмом (рис. 1) строится таблица, в которую заносятся статистические данные, отражающие чистую прибыль предприятия АПК на исследуемом пятилетнем интервале времени, разбитом на равные части (кварталы). По исходным данным строится таблица разделенных разностей (рис. 1, блок 2). Так как исследуется деятельность предприятия за последний пятилетний период, то чистую прибыль организации в предыдущие годы логично не учитывать. Поэтому и скорость изменения чистой прибыли x(t) за этот промежуток времени, соответственно, равна нулю.
Используя данные последнего года исследуемого временного периода, а также минимум и максимум разделенных разностей, необходимо построить таблицу характеристик расчётных данных (рис. 1, блоки 3–4).
Далее определяется аналитическое задание границ прибыли предприятия:
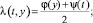
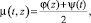
где λ(t, y) и μ(t, z) – максимальная и минимальная границы прибыли предприятия соответственно. Приближение функций φ(х) и ψ(t) для минимальных и максимальных значений чистой прибыли разделенных разностей необходимо определять в форме
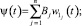
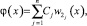
где Bj и Cj – максимальная и минимальная граница коэффициента скорости изменения прибыли соответственно; w1j(t), w2j(x) – системы функций для построения конуса (области) решений относительно прибыли предприятия (выбранные, согласно заданным условиям); t – время расчета (месяц); x – полученная прибыль (в расчётном месяце). На следующем шаге осуществляется построение функций λ = λ(t, x), μ = μ(t, x), которые удовлетворяют условиям: λ(t, x), μ(t, x) ≥ 0; λ(t, 0), μ(t, 0) ≡ 0. В результате, по выбранной системе функций:
,
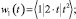
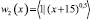методом наименьших квадратов строится аналитическая зависимость λ(t, x). Для функции μ(t, x), при статистических значениях прибыли, необходимо использовать следующую систему уравнений:
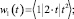
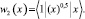
Реализуя метод наименьших квадратов, в пакете программ MathCad можно автоматизировать вышеприведённую вычислительную процедуру. Это позволяет оперативно построить максимальную границу значения прибыли предприятия λ(t, x):
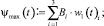
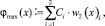
где ψmax(t) и φmax(х) – максимальные скорости изменения объёма полученной прибыли. При этом матрица В содержит коэффициенты функции ψ = ψ(t), а матрица С – φ = φ(х). Функции ψ = ψ(t), φ = φ(х) записываются линейной комбинацией своих аргументов временного периода t и значения прибыли x: Они представляются следующим образом:
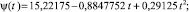
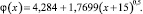
Рис. 1. Алгоритм реализации метода Е.В. Воскресенского
Аналогично строим функцию μ = μ(t, x) для которой зависимости минимальных скоростей изменения объёма полученной прибыли ψmin(t) и φmin(х) примут следующий вид:
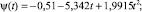
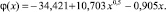
Следующим расчётным этапом является определение решения y(t) и z(t) для соответствующих скалярных уравнений
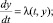
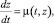
где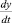 
и 
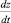– верхняя и нижняя границы полученной прибыли соответственно, полученные в результате вычислений методом Рунге – Кутты на временном (двухлетнем) отрезке 
.
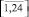Далее (в соответствии с блоками 5–6, рис. 1), строится график, отображающий динамику изменения чистой прибыли предприятия АПК в границах максимальных и минимальных значений за исследуемый период (рис. 2).
Следующим алгоритмическим действием является ввод функции управления u(t, x), позволяющей выполнить анализ свойств скорости изменения чистой прибыли с учетом введения данного управления x(t: t0, x0, u) на следующий временной период, где t0 – начальный период времени; x0 – начальное значение прибыли; u(t, x) – функция управления за счет дополнительного финансирования за промежуток времени t (рис. 1, блок 7). Применяя функцию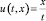 
, получаем промежуточный (оценочный) результат в виде расчетных показателей объёма чистой прибыли предприятия (рис. 1, блок 8). В соответствии с блоком 9 алгоритма (рис. 2) определяются приближения φ(х) и ψ(t) для минимальных и максимальных значений разделенных разностей. В результате строим функции λ1 = λ1(t, x), μ1 = μ1(t, x), где λ1(t, x) и μ1(t, x) – максимальная и минимальная границы значений возможной прибыли предприятия соответственно. Обе функции при решении данной задачи удовлетворяют условиям квазимонотонного неубывания. Далее по системе функций:
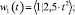
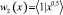
методом наименьших квадратов строится аналитическое задание функции λ1(t, x). Для функции μ1(t, x) используется следующая система функций:
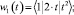
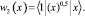
На следующем шаге осуществляется построение функции λ1 = λ1(t, x). В результате получаются уравнения
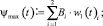
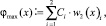
где Bi и Ci – соответственно максимальная и минимальная границы прогнозируемого значения коэффициента скорости изменения прибыли. При этом матрица В содержит коэффициенты функции ψ = ψ(t), а матрица С – φ = φ(х). Далее определяем функции максимальной и минимальной скорости изменения объёма прогнозируемой прибыли предприятия ψ = ψ(t), φ = φ(х), представленные линейной комбинацией своих аргументов: ψ(t) = 2,14 – 0,0326·2,5·t2, φ(х) = 0,2166 + 0,57·х 0,5. На следующем шаге, методом Рунге – Кутты на отрезке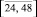 
находятся решения y1(t) и z1(t), соответствующие скалярным уравнениям: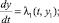 
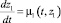– (рис. 1, блок 10), где 
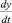и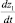 
– верхняя и нижняя границы возможной прибыли.
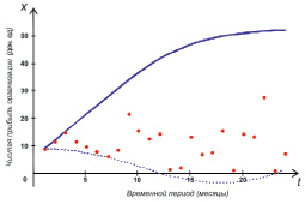
Рис. 2. Динамика изменения чистой прибыли предприятия АПК в границах максимальных и минимальных значений
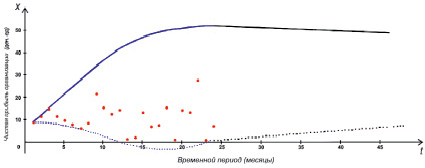
Рис. 3. Прогнозирование и управление динамикой изменения чистой прибыли на перспективный период
По результатам вычислительных процедур строится график (рис. 3), отображающий характер поведения решений уравнений сравнения.
Необходимо отметить, что в настоящее время фактическое применение современных математических методов для перспективного определения финансово-экономической устойчивости отечественных производственных предприятий АПК осуществляется не в полной мере [4]. Поэтому программы подготовки и переподготовки специалистов руководящего звена предприятий отрасли должны включать вопросы, связанные с экспертно-информационным обеспечением на основе передовых методов и моделей анализа и прогнозирования экономики организации для компетентностного и своевременного принятия управленческого решения [5].
Заключение
Таким образом, в условиях современного производства моделирование долгосрочного экономического прогноза методами нелинейной динамики находит все большее практическое применение. Проведённый комплексный анализ математических методов исследования финансово-экономической деятельности производственных предприятий агропромышленного комплекса показал, что наиболее приемлемым для решения поставленной задачи является метод дифференциальных включений Е.В. Воскресенского. Программы подготовки и переподготовки специалистов руководящего звена предприятий отрасли должны включать вопросы, связанные с системами поддержки и принятия решений на основе передовых методов и моделей анализа и прогнозирования рентабельности организации.