В работе [1] предложена методика синтеза адаптивных систем управления на основе метода скоростного биградиента с алгоритмами адаптации параметров многообразия скольжения в дифференциальной форме. При реализации этих алгоритмов требуется блок интеграторов размерности вектора настраиваемых параметров. В данной работе предлагается использовать алгоритмы адаптации в конечной (недифференциальной) форме. Для линейных объектов управления представлена постановка задачи слежения с явной эталонной моделью конечного каскада. Рассмотрена методика синтеза класса алгоритмов адаптивного управления, сформулированы условия работоспособности алгоритмов. Приведены результаты анализа качества замкнутой системы с гладкими и релейными алгоритмами скоростного биградиента с подсистемой адаптации математического моделирования.
Постановка задачи
Рассматривается каскадная модель объекта управления (ОУ), состоит из подсистемы вывода S1 и подсистемы ввода S2 в регулярной форме
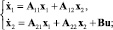
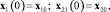(1)
где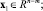 
x2 ∈ Rm; u ∈ Rm – векторы состояния подсистем и управления соответственно; Aij(ξ) (i, j = 1, 2), B2(ξ) – постоянные матрицы, причем det B2 ≠ 0; ξ ∈ Ξ – множество вариантов неизвестных параметров объекта управления (ОУ).
Целью управления является ограниченность всех траекторий системы и достижения целевого неравенства
Q(e) ≤ Δe при t ≥ t*, (2)
где Δe ≥ 0; t* ≥ 0; Q(e) – локальный (неинтегральный) целевой функционал вида
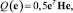(3)
где e = x1 – x1 – ошибка слежения; xЭ1 – желаемое состояние подсистемы S1, H = HT > 0.
Зададим желаемую динамику для конечного каскада с помощью явной эталонной модели вида
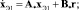
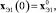(4)
где A* – гурвицевая матрица; r – гладкая, ограниченная, вместе со своей производной вектор-функция.
Синтез алгоритмов адаптации в конечной форме
Проведем синтез алгоритма управления методом скоростного биградиента (МСБГ) [2].
Этап 1. На первом этапе в условиях полной априорной информации об объекте синтезируется «идеальное» виртуальное управление конечным каскадом, обеспечивающее достижение цели управления
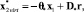(5)
где θ* = θ(ξ) – m×(n – m) матрица; D* = D(ξ) – m×n матрицы идеальных параметров.
Определим производную по времени от целевой функции (3) в силу уравнений системы (1), (4) с учётом (5) при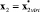 
:
(6)
Идеальные параметры θ*, D* выберем из условий
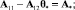
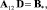(7)
так что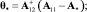 
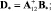
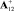– псевдообратная матрица.
Получаем
,
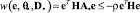где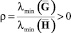 
– матрица H = HT > 0 удовлетворяет уравнению Ляпунова 
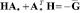. Следовательно, достигается цель управления x1 → xЭ1 при t → ∞. Из гурвицевости матрицы A* и ограниченности задающих воздействий 
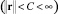следует ограниченность xЭ1, x1.
Этап 2. На втором этапе неизвестные параметры «идеального» виртуального управления заменяются настраиваемыми, и синтезируется алгоритм адаптации.
Заменим в выражении (5) идеальные параметры θ*, D* настраиваемыми θ, D. Получим виртуальное управление вида
x2virt = –θx1 + Dr. (8)
Вычислим производную по времени от целевой функции (3) в силу уравнений системы (1), (4) с учётом (8) при 
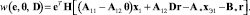
Вычисляя градиенты функции по настраиваемым параметрам θ, D от функции w(e, θ, D) и выбирая алгоритм адаптации в конечной форме (недифференциальной), получаем
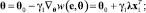
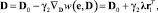(9)
где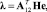 
γi > 0, 
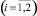– коэффициенты усиления алгоритмов адаптации; θ0, D0 – матрицы априорных оценок (могут быть выбраны нулевыми).
Этап 3. На третьем этапе формируется отклонение от пересечения гиперповерхностей в форме невязки между выходным сигналом входного каскада и виртуальным управлением. Синтезируется управление, обеспечивающее достижение многообразия гиперповерхностей.
Выберем отклонение от пересечения многообразий гиперповерхностей σ ≡ 0 в форме невязки между входом подсистемы S2 и настраиваемым виртуальным управлением x2virt так, что
σ = x2 – x2virt. (10)
Введем дополнительный целевой функционал (ЦФ), характеризующий отклонение траектории системы от пересечения многообразий
R(σ) = 0,5σTσ. (11)
Вычислим скорость изменения ЦФ (11)
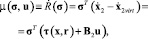(12)
где
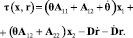
Семейство алгоритмов, обеспечивающее достижение целевого неравенства
R(σ) ≤ Δσ при t ≥ tσ, (13)
имеет вид [3, 4]
u = u0 – γmφ(σ), (14)
где u0 – априорное заданное управление, которое может быть равно нулю; вектор-функция φ(σ) ∈ Rm удовлетворяет условию усиленной псевдоградиентности:
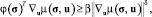
где β > 0, δ = 1, 2, ... – некоторые числа;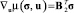 
– градиент функции μ(σ, u) по управлению u.
Условию усиленной псевдоградиентности удовлетворяют, например, функции
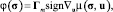
при δ = 1,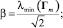 
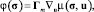при δ = 2, β = λmin(Γm),
где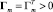 
– (2×2) матрицы усилителя; λmin(Γm) – минимальное собственное значение Γm.
При u = 0 получаем гладкие и релейные алгоритмы вида
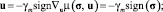(15)
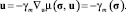(16)
Заметим, что алгоритм (15) относится к классу систем с настраиваемым скользящим режимом [2, 5].
Утверждение. Для системы (1), (4), (8), (9), (10) с алгоритмом управления (15) или (16) справедливы следующие утверждения:
1. Для системы с алгоритмом управления (15) существуют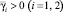 
, 
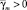такие, что при 
, 
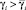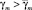цели управления (2), (13) достигаются при любых Δe > 0, Δσ > 0, все траектории системы ограничены. Существует момент времени t*, такой, что R(σ(t)) ≡ 0 (σ(t) ≡ 0) при t ≥ t*. При γi → ∞ цель управления (2) предельно достижима, т.е. Q(e) → 0 при t → ∞.
2. Для системы с алгоритмом управления (16) существуют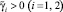 
, 
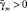такие, что при 
, 
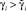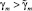цели управления (2), (13) достигаются при любых Δe > 0, Δσ > 0, все траектории системы ограничены. При γi → ∞, γm → ∞ справедливо R(σ) → 0, Q(e) → 0 при t → ∞.
3. Для замкнутых систем с алгоритмами (15), (16) существует функция Ляпунова вида
V(e, σ, θ) = Q(e) + R(σ). (17)
Из утверждения следует, что гладкий алгоритм управления обладает более слабыми свойствами сходимости, поэтому его предпочтительнее использовать в комбинации с релейным алгоритмом. При этом в замкнутой системе достигается асимптотическая устойчивость (e, σ) → ∞ при t → ∞.
Пример и результаты моделирования алгоритмов управления с адаптацией в конечной форме
Пусть объект управления описывается уравнением
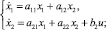
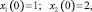
где aij (i, j = 1, 2), b2 – параметры ОУ (b2 > 0, a12 > 0).
Цель управления
Q(e) ≤ Δe при t ≥ t*,
где e = x1 – xЭ1.
Желаемое поведение системы в соответствии c (4) зададим уравнением
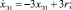xЭ1(0) = –1,
где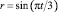 
– задающее воздействие.
Алгоритм адаптации в конечной форме имеет вид
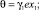
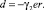
Алгоритм управления
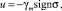
где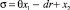 
, γm > 0.
На рис. 1–5 приведены результаты моделирования системы с алгоритмом адаптивного управления при начальных условиях θ(0) = –0,5; d(0) = 0,1 параметрах объекта управления a11 = 1, a12 = 2, a21 = 1, a22 = 3, b2 = 1, параметрах адаптера для конечной формы γ1 = 22, γ1 = 35.
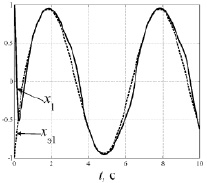
Рис. 1. Графики выходного сигнала объекта управления и эталонной модели
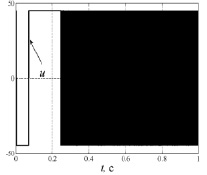
Рис. 2. Графики управления
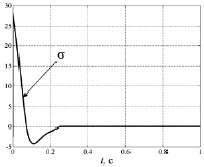
Рис. 3. Графики отклонений от многообразия гиперповерхностей
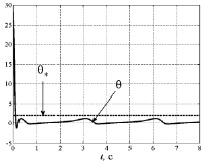
Рис. 4. Графики идеальных θ* и настраиваемых θ параметров
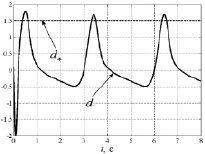
Рис. 5. Графики идеальных d* и настраиваемых d параметров
Результаты математического моделирования системы с управлением в релейной форме с конечным алгоритмом адаптации многообразия скольжения подтверждают достижение цели управления (ограниченность траектории и обеспечения желаемой динамики конечного каскада с конечной точностью). Повышение точности слежения может быть обеспечено увеличением коэффициентов усиления контура адаптации (γ1, γ2). Алгоритмы адаптации параметров многообразия скольжения не обладают идентифицирующими свойствами.
Заключение
В работе представлена методика синтеза адаптивных систем управления для линейных объектов на основе скоростного биградиента с алгоритмами адаптации параметров многообразия скольжения в конечной (недифференциальной) форме. Алгоритм адаптации в конечной форме обеспечивает быстрое (по сравнению с алгоритмами адаптации в дифференциальной форме [1]) парирование координатных возмущений (ошибки слежения) конечного каскада. Релейный алгоритм управления обеспечивает возникновение в замкнутой системе настраиваемого скользящего режима. Гладкий алгоритм обеспечивает стремление траекторий замкнутой системы в ε – окрестность настраиваемого многообразия и асимптотическое стремление к многообразию при бесконечно большом коэффициенте усиления. Поэтому предпочтительно использовать гладкий алгоритм в сумме с релейным алгоритмом.
Работа выполнена при финансовой поддержке РФФИ и Правительства Калужской области (грант № 14-48-03115).