Архитектура зданий всегда имела большое значение в сознании людей. Постройки делали величественными и масштабными, показывая тем самым мощь и силу государства или отдельно взятого человека. Но это появилось чуть позже. Изначально человек пытался решить проблему защиты от неблагоприятных природных условий, но со временем, когда ответ на этот вопрос был найден, появилась проблема гармонизации и эстетики созданного искусственного пространства. Появились первые стилистические приемы и закономерности.
Марк Витрувий в «Десяти книгах об архитектуре» [1] пытался осветить вопрос о пропорциональности и ввел понятие «эвритмия». Он пишет так: «Эвритмия – это приятное глазу расположение целого, которое получается при правильном соотношении ширины, высоты и длины отдельных его частей при соблюдении общих симметрических отношений».
Философ Древней Греции Пифагор один из первых, кто математически разбирает существо гармонических отношений. Аристотель основными требованиями красоты выдвигает порядок, симметрию (т.е. пропорциональность) и ограниченность в размерах. Порядок требует определенных, не случайных соотношений размеров отдельных частей между собой и к целому. Аристотель, как и Платон, признавал красоту правильных фигур и значение пропорции, устанавливающей правильное отношение между тремя и четырьмя величинами [2].
В архитектуре древней Греции и Рима все подчинялось точным математическим пропорциям и законам. Рассчитанное греками «золотое сечение» легло в основу всех знаменитых памятников архитектуры [4]. Использование законов пропорциональности в современном строительстве так же необходимо и актуально, как и сотни лет назад.
В современном строительстве и проектировании зданий большое значение уделяется энергоэффективности. Этот аспект очень важен на сегодняшний день, поскольку стоимость энергоресурсов высока, и неэффективное их использование приводит к неразумным затратам, как материальным, так и природным.
Согласно Федеральному закону № 261-ФЗ «Об энергосбережении и о повышении энергетической эффективности и о внесении изменений в отдельные законодательные акты Российской Федерации» [7] наружные стены строящихся и реконструируемых зданий должны удовлетворять требованиям СП 50.13330.2012 «Тепловая защита зданий» [6]. Проектировщики решают эту задачу, используя различные многослойные конструкции и новые композитные материалы. Но мостики холода остаются, и часть энергии, затрачиваемой на отопление здания, выходит в атмосферу. Данный вопрос интересен для нас. Его можно решить разными путями. Один из них заключается в применении в отделке фасадов архитектурных элементов.
Для энергосбережения идеальной была бы ситуация, когда теплоизоляция устроена непрерывно по всему зданию. Но существуют места, где теплоизоляционную оболочку приходится прерывать. Это различные стыки стен, углы зданий, выступающие балки и плиты, оконные и дверные перемычки, навесы, эркеры, выходящие наружу окончания бетонных элементов и другое. Выявить мостики холода можно, исследуя здания тепловизором. Основной характеристикой, определяющей теплозащитные свойства ограждения зданий, является термическое сопротивление R [8]. Исследованию теплофизических свойств наружных ограждений посвящены работы и патенты [5].
В существующих зданиях присутствуют, как правило, оба типа мостиков холода (конструктивные и геометрические). Они могут стать огромной проблемой для здания. Во-первых, через них происходят большие теплопотери, приводящие к повышенному энергопотреблению. Во-вторых, существует возможность накопления водного конденсата. В-третьих, существует риск повреждения строительных элементов. В-четвертых, из-за накапливающейся влаги есть вероятность появления плесневого грибка, приводящего к различным заболеваниям. Этот вопрос мы не могли оставить без внимания. И как один из вариантов решения данной проблемы предлагаем использовать архитектурные элементы, которые могут выполнять сразу две функции: эстетическую (архитектурную) и теплозащитную.
Кто-то может подумать, что, предлагая архитектурные элементы, мы ограничиваем творческий поиск архитекторов. Рассмотрев и проанализировав существующие материалы и конструкции, пришли к выводу, что это не так. С помощью различных элементов можно сделать объекты ярче и интереснее, а классические элементы могут гармонично вписаться в существующую застройку при реконструкции исторической части города [3].
В качестве примера предлагаем рассмотреть оконный узел (рис. 1) с мостиками холода и подобрать для него подходящие архитектурные элементы, основываясь не только на теплозащитных свойствах, но и на пропорциональной зависимости и гармонии. Для этого оконный узел условно рассекаем пятью плоскостями (рис. 1) и производим расчет термического сопротивления стенового ограждения по толщине (табл. 1).
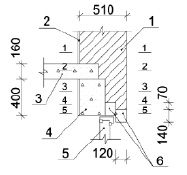
Рис. 1. Чертеж оконного узла: 1 – кирпичная стена; 2 – штукатурка; 3 – железобетонное перекрытие; 4 – железобетонная перемычка; 5 – оконный блок; 6 – железобетонная перемычка
Находим термическое сопротивление для каждого из сечений по формуле:
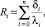(1)
где Ri – термическое сопротивление i-го слоя, (м2·°С)/Вт; δi – толщина i-го слоя, м; λi – коэффициент теплопроводности i-го слоя, Вт/(м·°С).
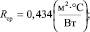
Rср < R1 (0,434 < 0,697).
Таблица 1
Теплотехнические характеристики материалов конструктивных элементов оконного узла
|
Наименование |
δ, толщина слоя, м |
λ, коэффициент теплопроводности, Вт/(м·°С) |
R, сопротивление теплопередачи сечения, (м2·°С)/Вт |
|
Сечение 1-1 |
|||
|
Штукатурка |
0,02 |
0,76 |
0,697 |
|
Кирпичная кладка |
0,51 |
0,76 |
|
|
Сечение 2-2 |
|||
|
Железобетонная плита |
0,12 |
1,92 |
0,576 |
|
Кирпичная кладка |
0,39 |
0,76 |
|
|
Сечение 2-2 с архитектурным элементом |
|||
|
Пенополистирол |
0,10 |
0,04 |
3,076 |
|
Сечение 3-3 |
|||
|
Штукатурка |
0,02 |
0,76 |
0,482 |
|
Железобетонная балка |
0,27 |
1,92 |
|
|
Кирпичная кладка |
0,24 |
0,76 |
|
|
Сечение 3-3 с архитектурным элементом |
|||
|
Пенополистирол |
0,08 |
0,04 |
2,482 |
|
Сечение 4-4 |
|||
|
Штукатурка |
0,02 |
0,76 |
0,387 |
|
Железобетонная балка |
0,27 |
1,92 |
|
|
Железобетонная перемычка |
0,12 |
1,92 |
|
|
Кирпичная кладка |
0,12 |
0,76 |
|
|
Сечение 4-4 с архитектурным элементом |
|||
|
Пенополистирол |
0,06 |
0,04 |
1,887 |
|
Сечение 5-5 |
|||
|
Штукатурка |
0,02 |
0,76 |
0,292 |
|
Железобетонная балка |
0,27 |
1,92 |
|
|
Железобетонная перемычка |
0,24 |
1,92 |
|
|
Сечение 5-5 с архитектурным элементом |
|||
|
Пенополистирол |
0,05 |
0,04 |
1,542 |
Выполнив расчет термического сопротивления стенового ограждения по толщине без архитектурного элемента, мы выявили, что если сравнивать R1 сечения 1-1 с R2, R3, R4, R5 сечений 2-2, 3-3, 4-4, 5-5, то значения термического сопротивления значительно ниже и не соответствуют значению всей стены R1. Если сравнить среднее значение термического сопротивления Rср сечений 2-2, 3-3, 4-4, 5-5 с R1 сечения 1-1, то также выясняется сильное расхождение значений. На основе этого можем сделать вывод, что в данном узле возникает мостик холода.
Следующим этапом анализа является рассмотрение оконного узла с архитектурным элементом из пенополистирола (рис. 2). По аналогии с предыдущим производим расчет термического сопротивления стенового с архитектурным элементом (табл. 1).
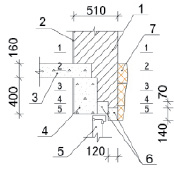
Рис. 2. Чертеж оконного узла с архитектурным элементом: 1 – кирпичная стена; 2 – штукатурка; 3 – железобетонное перекрытие; 4 – железобетонная перемычка; 5 – оконный блок; 6 – железобетонная перемычка; 7 – архитектурный элемент
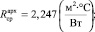
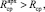(2,247 > 0,434);
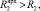(3,076 > 0,576);
(2,482 > 0,482);
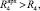(1,887 > 0,387);
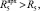(1,542 > 0,292);
Выполнив расчет термического сопротивления стенового ограждения с архитектурным элементом по толщине, мы выявили, что если сравнивать сечение 1-1 с сечениями 2-2, 3-3, 4-4, 5-5, то значения термического сопротивления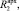 
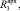
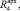
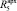значительно выше значения всей стены R1. Это говорит о том, что благодаря архитектурному элементу из пенополистирола, мы добились повышения значения термического сопротивления всего оконного узла, тем самым избавились от проблемы «мостика холода».
Далее составляем сравнительную таблицу (табл. 2) для архитектурных элементов из различных теплоизоляционных материалов. В таблице сравниваются значения δср – средняя толщина элемента, Rср архитектурного элемента, S – площадь сечения элемента, R единицы площади элемента. Из тех нами выбранных теплоизоляционных материалов архитектор может задать любую архитектурную форму элемента и, зная (R) единицы площади и площадь сечения (S) архитектурного элемента, может найти необходимое для расчета Rср архитектурного элемента.
На основании таблицы вычерчиваются оконные узлы с архитектурными элементами из различных материалов (рис. 3).
Выполнив расчеты и вычертив узлы с архитектурными элементами, необходимо выявить закономерности их применения, используя математические пропорции. Для этого вводим модуль М, равный 50 мм. Это число выбрано на основе минимальной толщины архитектурного элемента, а также с учетом кратности деления.
Установим математическую закономерность применения архитектурного элемента в соответствии с толщиной, используя предлагаемые нами формулы:
lmin = k·Ф·h; (2)
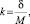(3)
где lmin – минимальная ширина оконного проема, м; k – коэффициент пропорциональности; δ – толщина архитектурного элемента, м; М – модуль, равный минимально возможной толщине утеплителя, м; Ф = 1,62 – коэффициент «золотого сечения»; h – высота утеплителя (h = 0,63 м принято исходя из конструкции оконного узла).
Применим формулы (2), (3) для архитектурных элементов из пенополистирола или пенополиуретана. Получаем минимальную ширину lmin оконного проема. Затем вычерчивается оконный узел с архитектурным элементом и варианты возможных профилей (рис. 4).
lmin = k·Ф·h = 1·1,62·0,63 = 1,02 м.
Рекомендуется применять данные материалы для индивидуальных жилых домов, многоквартирных жилых домов, а также общественных зданий. Ширина оконного проема должна соответствовать 1 метру и более.
Таблица 2
Теплофизические характеристики материалов, используемых для теплозащитного архитектурного элемента
|
Материал |
λ коэффициент теплопроводности, Вт/(м·°C) |
δср, м |
Rср архитектура элемента, (м2·°C)/Вт |
S сечения, м2 |
R единицы площади, (м2·°C)/Вт |
|
Пенополистирол ПС-Б |
0,04 |
0,077 |
1,93 |
0,06 |
0,321 |
|
Пенополиуретан |
0,029 |
0,06 |
2,07 |
0,05 |
0,414 |
|
Газобетон |
0,13 |
0,17 |
1,31 |
0,11 |
0,119 |
|
Пенобетон |
0,18 |
0,20 |
1,11 |
0,12 |
0,093 |
|
Пеностекло |
0,07 |
0,1 |
1,43 |
0,07 |
0,204 |
|
Полистиролбетон |
0,15 |
0,18 |
1,20 |
0,12 |
0,1 |
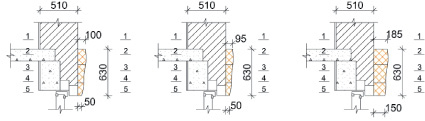
а б в
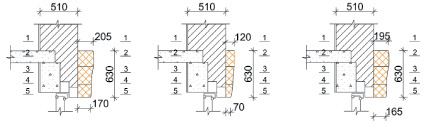
г д е
Рис. 3. Оконный узел с элементом из: а – пенополистирола; б – пенополиуретана; в – газобетона; г – пенобетона; д – пеностекла; е – полистиролбетона
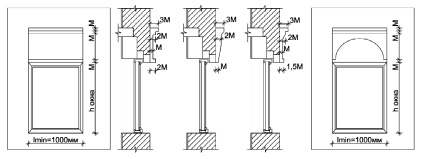
Рис. 4. Оконный узел с элементом из пенополистирола или пенополиуретана
Применим формулы (2), (3) для архитектурных элементов из пеностекла. Получаем минимальную ширину lmin оконного проема, для которого наиболее целесообразна полученная толщина архитектурного элемента. Затем вычерчивается оконный узел с архитектурным элементом и варианты возможных профилей (рис. 5).
lmin = k·Ф·h = 1,5·1,62·0,63 = 1,5 м.
Рекомендуется применять пеностекло для индивидуальных жилых домов, многоквартирных жилых домов, а также общественных зданий. Ширина оконного проема должна соответствовать 1,5 метра и более.
Применим формулы (2), (3) для архитектурных элементов из газобетона, пенобетона и полистиролбетона. Получаем минимальную ширину lmin оконного проема, для которого наиболее целесообразна полученная толщина архитектурного элемента. Затем вычерчивается оконный узел с архитектурным элементом и варианты возможных профилей (рис. 6).
lmin = k·Ф·h = 3·1,62·0,63 = 3 м.
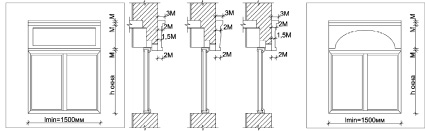
Рис. 5. Оконный узел с элементом из пеностекла
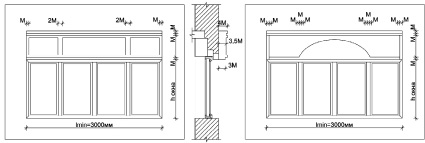
Рис. 6. Оконный узел с элементом из газобетона, пенобетона и полистиролбетона
Выполнив расчеты и выявив закономерность применения архитектурных элементов окон из различных теплоизоляционных материалов, мы еще раз доказываем взаимосвязь математических закономерностей с архитектурной выразительностью.
Рекомендуется применять газобетон, пенобетон и полистиролбетон для индивидуальных жилых домов, а также общественных зданий. Ширина оконного проема должна соответствовать 3 метрам и более.
Решая проблему энергоэффективности оконного узла, мы смогли не только повысить теплозащитные качества, но и выявить возможность применения архитектурных элементов из различных теплоизоляционных материалов, тем самым делая здание выразительным и интересным. Выбор утеплителя должен производиться не только исходя из его чисто утилитарных свойств (чем толще, тем лучше), но и с учетом требований пропорциональности и гармонии.