Целью работы является автоматизация расчетов сопряжения бьефов водосливной плотиной с водосливом практического профиля в пространственных условиях. Предметом исследования является моделирование руслового потока в пространственных условиях в информационной среде MathCAD. Для исследования использованы методы гидравлики открытых водотоков и гидротехнических сооружений на основе информационных технологий. Произведен расчет свободного растекания потока при сопряжении бьефов водосливом практического профиля в среде MathCad на примере Чебоксарской ГЭС. Расчетный максимальный расход ГЭС определяется по кривой связи расходов и уровней воды в нижнем бьефе в зависимости от уровня воды в Камском устье [4, 5].
Параметры моделирования
При расчете приняты следующие характеристики нижнего бьефа [4, 5]: ширина плотины B := 144,5 м; ширина фронта водосливных отверстий bo := 20 м; число водосливных отверстий n := 6; высота порога водослива относительно рисбермы P := 14 м; отметка рисбермы БС Δp := 40 м; максимальный уровень нижнего бьефа УНБ := 55,3 м; отметка концевого крепления Δк := 31,5 м; строительная отметка грунта Δг := 28,6 м; высота падения струи z := Δк – Δг, z := 2,9 м; суммарная ширина фронта n водосливных отверстий b := nbo, n := 120 м; ускорение свободного падения g := 9,81 м/с2.
Численное моделирование в среде MathCAD
На основании кривой связи установлена зависимость уровня от расхода [4, 5]:
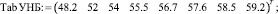
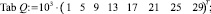
Сплайн-интерполяция зависимости уровня H от расхода Q имеет вид
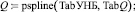
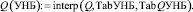
Расчетный максимальный расход ГЭС Q(УНБ) = 1,243∙104 м3/с. Доля расчетного расхода плотины от расхода ГЭС ε = 0,5. Расход через плотину Qn := ε∙Q(УНБ), Qn = 6,213∙103 м3/с. Расход через отверстие при НПУ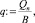 
q = 43 м3/c. Относительная ширина потока на плотине 
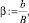β = 0,83. Отметка НПУ := 63 м. Напор на пороге водослива H0 := НПУ – PП – Δp, H0 = 9 м. Энергия перед сооружением относительно дна водобоя T0 := PП + H0, T0 = 23 м. Коэффициент скорости φ := 0,95. Начальное значение критической глубины 
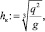hк = 5,733 м. Коэффициент энергии потока 
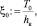ξ0 = 4,012. Связь коэффициента сжатия 
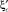с коэффициентом 
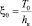имеет вид 
.
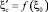Вектор-столбец значений коэффициента кинетической энергии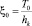 
имеет вид
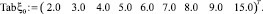
Вектор-столбцы значений коэффициента сжатия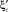 
имеют вид:
– при коэффициенте скорости φ = 0,80
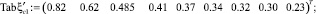
– при коэффициенте скорости φ = 0,85
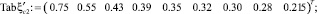
– при коэффициенте скорости φ = 0,90
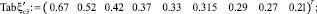
– при коэффициенте скорости φ = 0,95
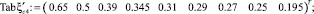
– при коэффициенте скорости φ = 1,00
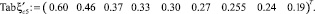
Коэффициент сжатия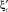 
от коэффициента 
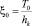имеет вид
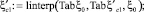
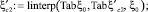
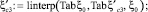
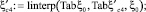
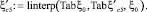
Табличные значения связи коэффициента сжатия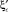 
с коэффициентом скорости φ [3] имеют вид матричных строк:
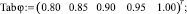
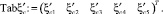
В результате строится сплайн-интерполяция функции коэффициента сжатия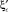 
от коэффициента скорости
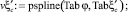
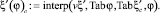
Значение коэффициента сжатия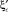 
при заданной величине коэффициента скорости φ равно 
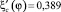. Связь 
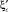с φ выражается постоянной величиной.
Первая сопряженная глубина h1 := ξ′∙hк, h1 = 2,233 м. Глубина в сжатом сечении hc := h1, hc = 2,223 м. Коэффициент кинетичности потока α := 1. Число Фруда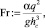 
Fr = 16,926. Коэффициент формы струи равен 
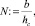N = 53,739.
Коэффициент, учитывающий неравномерность распределения удельного расхода по сечению k := 0,8 – (0,8 – β), k = 0,73 [2]. Предельная бытовая глубина, обеспечивающая свободное растекание,
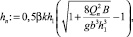hn = 9,759 м.
Критическая глубина
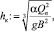hк = 5,733 м.
Минимальная бытовая глубина, при которой образуется одна область растекания, hб.min := 1,3hк, hб.min = 7,453 м. Глубина, при которой появляется совершенный прыжок в конце листовидной области растекания, h2 := 1,5hк, h2 = 8,6 м. Тангенс угла растекания
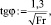tgφ = 0,316.
Угол растекания равен
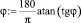[1], φ = 17,536 град.
Расстояние от выходного сечения до сечения полного растекания
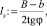ls = 38,768 м.
Общая длина листовидной области растекания
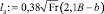[3], lл = 286,8 м.
Глубина в конце листовидной области
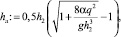hл = 3,594 м.
Скорость в конце листовидной области растекания
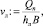vл = 11,963 м/с.
Скорость равномерного движения в отводящем русле
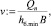vл = 5,769 м/с.
Длина переходной зоны Б
lб := 65(hк – hл) [2], lб = 139,045 м.
При этом скорости уменьшаются от vл = 11,963 м/с до v = 5,769 м/с. Площадь живого сечения в створе с критической глубиной
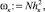ωк = 1,766∙103 м2.
Площадь сечения в створе первой сопряженной глубины
ω1 := bh1, ω1 = 267,96 м2.
Длина перехода в спокойное состояние
ln := 16,7(hк – h1) [1], ln = 58,456 м.
Табличные значения связи угла расширения струи α с относительной шириной фронта водосливных отверстий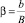 
:
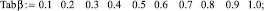
Далее производится сплайн-интерполяция зависимости угла расширения струи α с относительной шириной фронта водосливных отверстий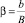 
.
Вектор кубического сплайна имеет вид
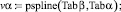
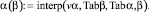
Угол расширения транзитной струи α(β) = 2,68 град. Тангенс угла расширения транзитной струи
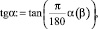tgα = 0,047.
Коэффициент заполнения русла
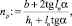[2], np = 25,251.
Критическая глубина
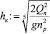[1], hк = 6,581 м.
Табличные значения зависимости средней глубины вдоль водосбросного фронта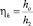 
с оптимальной глубиной нижнего бьефа 
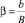при различных числах Фруда:
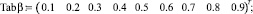
– число Фруда Fr = 50
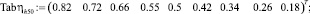
– число Фруда Fr = 30
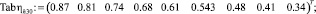
– число Фруда Fr = 20
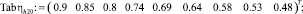
– число Фруда Fr = 10
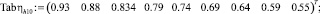
– число Фруда Fr = 5
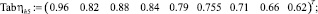
– число Фруда Fr = 2
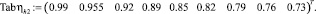
Линейная интерполяция зависимостей средней глубины по водосбросному фронту ηh от коэффициента оптимальной глубины нижнего бьефа β:
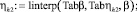
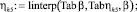
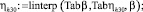
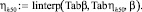
Табличные значения связи отношения средней глубины вдоль водосбросного фронта ηh с числом Фруда Fr имеют вид
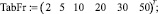
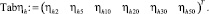
Вектор кубического сплайна зависимости средней глубины вдоль водосбросного фронта ηh от коэффициента оптимальной глубины нижнего бьефа β имеет вид
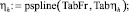
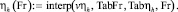
Параметр средней глубины вдоль водосбросного фронта η(Fr) = 0,538. Оптимальная вторая сопряженная глубина [2], при которой возникает спокойное сбойное течение,
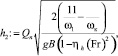h2 = 8,6 м.
Расчетная вторая сопряженная глубина h2 := 1,1h2, h2 = 15,574 м. Длина водобоя без гасителя
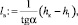lв = 92,897 м.
Табличные значения связи коэффициента сжатия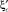 
с коэффициентом сжатия 
:
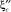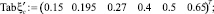
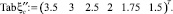
Сплайн-интерполяция зависимости коэффициентов сжатия потока на сопряженных глубинах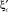 
и 
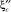реализуется в виде вектора кубического сплайна:
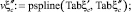
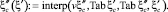
Вторая сопряженная глубина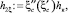 
h2ξ = 13,369 м. Вторая сопряженная глубина h2ξ = 13,369 меньше бытовой h2 = 17,131 или h2 < h2ξ, поэтому понижения дна водобоя и рисбермы не требуется.
При коэффициентах сжатия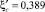 
и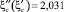 
параметр водобоя вычисляется по зависимости
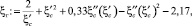
ξг = –0,34.
Если точка оказывается справа от кривой «самозатапливающихся» прыжков, при ξг = 1,2, то при коэффициенте сжатия ξс определяется величина
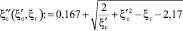[3],
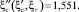
Высота сплошной стенки
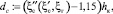dc = 2,642 м.
Высота стенки по проекту равна 4,0 м.
Далее приводится проверка выполнения условия беспрыжкового сопряжения за водобойной стенкой. Прежде всего выбираются варианты схем сооружения: истечение из донных отверстий – вариант_1 := 0; перепады без щитов – вариант_2 := 0; перепады со щитами – вариант_3 := 0; водосливы плавной формы без щитов – вариант_4 := 0; водосливы плавной формы со щитами – вариант_5 := 1.
φз = 0,9.
Глубина за водобойной стенкой в сжатом сечении
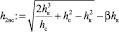[3], h2вс = 9,264 м.
Энергия потока за водобойной стенкой относительно дна водобоя
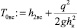[3], T0вс = 11,44 м.
При глубине hб, равной глубине за водобойной стенкой hб := h2вс, hб = 9,264 м, параметры Mвс и Nвс уравнения для глубины в сжатом сечении равны
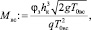Mвс = 0,683;
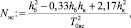[3], Nвс = 1,22.
Уравнение для относительной глубины в сжатом сечении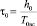 
решается с помощью функции root при стартовом значении τ0 := 0,9
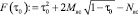[3],
τ0 := 0,9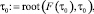 
τ0 = 0,938.
Отсюда глубина в сжатом сечении h0 := τ0T0вс, h0 = 10,728 м. Скорость потока за водобойной стенкой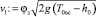 
[3], v1 = 3,364 м/с. Глубина в сжатом сечении 
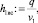h1вс = 12,78 м. Глубина в сжатом сечении за водобойной стенкой больше критической глубины, и сопряжение бьефов будет беспрыжковым. В этом случае за водобойной стенкой следует проектировать только рисберму.
Коэффициент расхода водослива m := 0,48. Длина водобоя
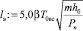[3], lв = 26,77 м.
Проектная длина водобоя равна 64 м.
Интерпретация результатов
Разработанная информационно-технологическая модель, реализованная в среде MathCAD, позволяет уточнить параметры сопряжения бьефов гидроузла за счет учета планового характера растекания потока в водоотводящем русле и автоматизировать процесс гидравлических расчетов. Применение информационных технологий создает условия для замены вычислений с помощью громоздких таблиц на расчеты гидравлических параметров потока с помощью сплайнов.
Выводы
Расчет сопряжения бьефов в пространственных условиях, выполненный на примере водосливной плотины Чебоксарской ГЭС, в информационной среде позволил установить численные значения максимального расхода ГЭС при снятии номинальной мощности. Найдены расходы водосливной плотины при различных значениях коэффициента скорости потока. Найдены скорости равномерного движения в отводящем русле, длина переходной области, угол расширения транзитной струи, значения первой и второй сопряженной глубин. Получены значения конструктивных параметров средств гашения энергии потока в нижнем бьефе. Сравнение результатов автоматизированных вычислений с данными проекта Чебоксарской ГЭС показало высокую адекватность предложенной методики.
Рецензенты:
Мануковский А.Ю., д.т.н., профессор кафедры промышленного транспорта, строительства и геодезии, ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова», г. Воронеж;
Алибеков С.Я., д.т.н., профессор кафедры электроснабжения и технической диагностики, ФГБОУ ВПО «Марийский государственный университет», г. Йошкар-Ола.