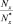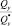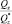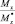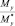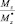Во многих курсах науки о сопротивлении материалов [1, 2, 3 и др.] рассматривают, как правило, следующие частные случаи сложного сопротивления стержня: косой изгиб, внецентренное сжатие (растяжение), изгиб с кручением. Влиянием поперечных сил на разрушение стержня при его сложном сопротивлении часто пренебрегают, считая это влияние несущественным. Проверку прочности стержня осуществляют, сопоставляя наибольшее нормальное (или эквивалентное) напряжение max|σ|, действующее в опасной точке стержня, с соответствующим опасным напряжением |σu| для материала. В настоящей работе предложена методика проверки прочности изотропных стержней, при нахождении в пространстве сил и моментов. Она является развитием работы [4].
На рис. 1 показаны ВСФ, действующие в поперечном сечении стержня: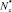 
– нормальная сила; 
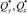– поперечные силы; 
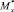– крутящий момент; 
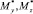– изгибающие моменты. При известном векторе ВСФ 
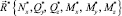необходимо определить соответствующий ему вектор прочности 
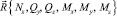и коэффициент запаса несущей способности рассматриваемого сечения
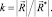(1)
На рис. 2 схематически изображена предельная поверхность (поверхность прочности) Σ в пространстве ВСФ. Здесь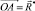 
– известный вектор ВСФ (например, из решения задачи о напряженно-деформированном состоянии стержня методами сопротивления материалов). 
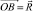– искомый вектор прочности, соответствующий вектору 
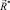. Очевидно, что векторы 
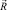и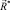 
должны лежать на одной прямой и быть одинаково направленными; их начала должны совпадать с началом координат в пространстве ВСФ.
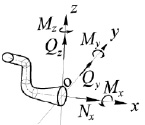
Рис. 1. ВСФ, действующие в поперечном сечении стержня
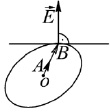
Рис. 2. Поверхность прочности Σ в пространстве ВСФ
Критерий достижения предельного состояния материала стержня запишем в следующем виде:
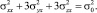(2)
Критерий (2) для стержней следует из критерия Мизеса [5], когда справедливы следующие гипотезы:
σyy = σzz = 0; εyz = εzy = 0.
Здесь σij, εij (i, j = x, y, z) – компоненты тензоров напряжений и деформации соответственно; σ0 – опасное значение нормального напряжения при линейном напряженном состоянии. В работе [4], исходя из уравнения (2) и используя жесткопластическую модель деформируемого твердого тела, получили следующие параметрические уравнения предельной поверхности в пространстве ВСФ для изотропных стержней:
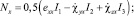
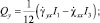
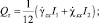
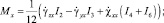(3)
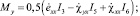
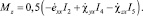
Параметрами в системе уравнений (3) являются отношения компонент вектора скоростей обобщенных перемещений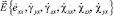 
. В общем случае эти параметры невозможно исключить из уравнений (3), используя для этой цели точные математические методы. В работе [4] приведены алгоритм построения различных сечений поверхности (3) и некоторые примеры построения таких сечений. Информация о сечениях поверхности (3) полезна, например, при решении задач о предельном состоянии стержневых конструкций (балок, ферм, рам) с применением кинематического и статического методов теории предельного равновесия [5] и аппарата математического программирования (см., например, работы [6, 7]). Различные сечения поверхности (3) могут быть полезными и при определении коэффициента запаса по несущей способности в частных случаях сложного сопротивления стержней. Например, имея сечения поверхности (3) координатной плоскостью NxOMx,, можно сравнивать соответствующие векторы 
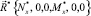и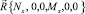 
при растяжении (сжатии) с кручением. Можно предположить, что область практических приложений уравнений (3) существенно расширится, если удастся использовать их при определении коэффициента запаса несущей способности в самом общем случае сложного сопротивления стержней. Ниже приведен вариант решения этой проблемы.
Компоненты коллинеарных векторов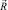 
и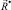 
удовлетворяют следующим равенствам:
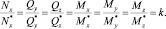(4)
Используя (4), можно записать следующую систему уравнений:
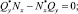
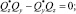
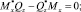(5)
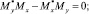
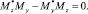
Подставив (3) в (5), получаем
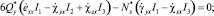
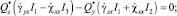
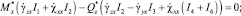(6)
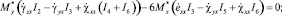
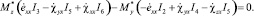
Так как в рассматриваемом случае существенное значение имеет только направление вектора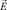 
, а его длина может быть произвольной, в качестве дополнительного к системе (6) примем уравнение
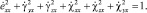(7)
Алгоритм определения коэффициента запаса по предельным состояниям изотропных стержней в общем случае их сложного сопротивления:
1. Определить вектор ВСФ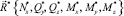 
в опасном сечении стержня.
2. Решить систему уравнений (6), (7) относительно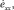 
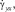
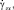
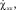
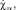
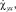т.е. найти вектор 
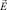, связанный с вектором прочности 
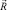ассоциированным законом [5] (рис. 2).
3. Используя формулы (3), по известному вектору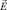 
определить соответствующий вектор прочности 
.
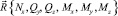4. Проверить выполнение условий (4).
5. Используя (1), определить коэффициент запаса прочности k изотропного стержня по методу предельных состояний.
Искомые компоненты вектора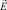 
присутствуют и в составе подынтегральных функций интегралов по площади поперечного сечения I1–I6 [4].
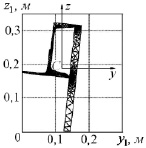
Рис. 3. Поперечное сечение составного стержня
Рассмотрим составной стержень, поперечное сечение которого показано на рис. 3. Прямоугольник имеет размеры 0,02×0,32 м, размеры швеллера соответствуют № 16, а равнобокого уголка – № 8. На рис. 3 представлен вариант разбиения сечения на конечные элементы – для численного вычисления интегралов I1–I6. Оси y, z – главные центральные оси сечения, y1, z1 – произвольные оси. Для этого стержня в работе [4] приведены некоторые сечения предельной поверхности (3).
С использованием программы, реализующей вышеописанный алгоритм, были получены результаты, приведенные в таблице. Строки 1–8 соответствуют сечению, изображённому на рис. 3; в них силы умножены на 103, моменты – на 104. Строки 9–14 соответствуют сечению, приведённому на рис. 4. Силы имеют размерность м2, моменты – м3.
В качестве второго примера рассмотрим определение коэффициентов запаса прочности для сечения крыла самолёта Ту-154 при различных сочетаниях заданных внутренних сил и моментов (рис. 4). Геометрические параметры крыла приведены на сайте http://www.twirpx.com/files/transport/aircrafting/ft.blueprint/. На рис. 4 выделена учитываемая при расчётах часть профиля крыла.
Предлагаемая методика проверки прочности стержней имеет следующие достоинства:
1. Исчезает необходимость выделения частных видов сложного сопротивления стержней (косой изгиб, изгиб с кручением и т.п.).
2. Все компоненты ВСФ, действующие в поперечном сечении стержня, на равных правах участвуют в процессе проверки прочности.
3. На форму и размеры стержня накладываются только самые общие ограничения, принятые в теории стержней.
4. Метод проверки прочности по предельным состояниям позволяет точнее определять коэффициент запаса прочности, чем метод расчета по допускаемым напряжениям – особенно в тех случаях, когда имеет место вязкое разрушение. В работе [8] отмечено: «Очевидно, что расчет по предельным нагрузкам дает существенно более правильное представление о прочности конструкции, чем расчет по максимальным напряжениям». Это утверждение справедливо и для отдельно взятых стержней.
Предлагаемая методика проверки прочности стержней по предельным состояниям может найти применение в практике расчетов и проектирования различных изделий.
Некоторые результаты определения k
|
№ п/п |
|
|
|
|
|
|
k |
|
1 |
5,2523 10,505 |
2,4208 4,8417 |
2,267 4,5339 |
1,4023 2,8047 |
3,8428 7,6857 |
0,3701 0,74019 |
0,5 |
|
2 |
–5,2523 –5,2523 |
–2,4208 –2,4208 |
–2,267 –2,267 |
–1,4023 –1,4023 |
–3,8428 –3,8428 |
–0,3701 –0,3701 |
1 |
|
3 |
5,3438 3,5625 |
2,2673 1,5115 |
2,1172 1,4114 |
1,9013 1,2676 |
3,6628 2,4419 |
0,39165 0,2611 |
1,5 |
|
4 |
–5,3438 –2,6719 |
–2,2673 –1,1336 |
–2,1172 –1,0586 |
–1,9013 –0,95066 |
–3,6628 –1,8314 |
–0,39165 –0,19582 |
2 |
|
5 |
1,3077 0,52307 |
0,67519 0,27007 |
1,5247 0,6099 |
3,0607 1,2243 |
4,0957 1,6383 |
1,2397 0,49587 |
2,5 |
|
6 |
–8,184 –2,728 |
–1,9351 –0,64505 |
–1,8908 –0,63028 |
–0,61323 –0,20441 |
–0,63986 –0,21329 |
–0,056516 –0,018839 |
3 |
|
7 |
–3,7883 –0,75766 |
2,0758 0,41515 |
–1,8939 –0,37878 |
0,21893 0,043785 |
–0,42052 –0,084104 |
0,088655 0,017731 |
5 |
|
8 |
3,7883 0,37883 |
–2,0758 –0,20758 |
1,8939 0,18939 |
–0,21893 –0,021893 |
0,42052 0,042052 |
–0,88655 –0,088655 |
10 |
|
9 |
808,3 538,87 |
–183,62 –122,41 |
127,53 85,018 |
8,28·106 5,52·106 |
2,00·106 1,33·106 |
3,69·107 2,46·107 |
1,5 |
|
10 |
–808,3 –404,15 |
183,62 91,81 |
–127,53 –63,764 |
–8,28·106 –4,14·106 |
–2,00·106 –9,99·105 |
–3,69·107 –1,85·107 |
2 |
|
11 |
47656 19062 |
7942,7 3177,1 |
7942,7 3177,1 |
–0,00010795 –4,32·10–5 |
0,00102 0,000408 |
–0,00037232 –0,00015 |
2.5 |
|
12 |
–47656 –15885 |
–7942,7 –2647,6 |
–7942,7 –2647,6 |
10,795·10–5 3,60·10–5 |
–0,00102 –0,00034 |
0,00037232 0,000124 |
3 |
|
13 |
753,26 215,22 |
–219,09 –62,598 |
93,55 26,728 |
8,28·106 2,37·106 |
2,0·106 5,71·105 |
3,70·107 1,06·107 |
3.5 |
|
14 |
–753,26 –188,31 |
219,09 54,773 |
–93,55 –23,387 |
–8,28·106 –2,07·106 |
–2,00·106 –5,00·105 |
–3,70·107 –9,24·106 |
4 |
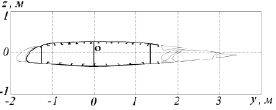
Рис. 4. Поперечное сечение крыла самолёта Ту-154
Рецензенты:
Габбасов Н.С., д.ф.-м.н., профессор, заведующий кафедрой математики, Набережночелнинский институт (филиал), Казанский (Приволжский) федеральный университет, г. Набережные Челны;
Хабибуллин Р.Г., д.т.н., профессор, заведующий кафедрой сервиса транспортных систем, Набережночелнинский институт (филиал), Казанский (Приволжский) федеральный университет, г. Набережные Челны.