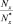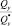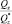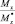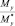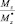Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сибгатуллин К.Э. 1 Сибгатуллин Э.С. 1

---

1 Набережночелнинский институт (филиал) Казанский (Приволжский) федеральный университет

Рассмотрены стержни произвольной формы, изготовленные из однородного изотропного материала. В общем случае в поперечном сечении стержня отличны от нуля все внутренние силовые факторы (ВСФ) – три силы и три момента. При известных значениях ВСФ определяется соответствующий вектор прочности в пространстве ВСФ и коэффициент запаса как отношение модуля вектора прочности к модулю вектора ВСФ. Расчётная модель базируется на гипотезах плоских сечений, малых деформаций, на соотношениях теории течения для жёсткопластического тела, использует постулат Друккера. Предлагаемые метод и алгоритм определения коэффициента запаса прочности, с использованием предельной комбинации ВСФ в сечении стержня, дают существенно более правильное представление о его прочности, чем соответствующий расчёт с использованием предельной комбинации напряжений в опасной точке этого сечения. Приведены примеры расчетов: составного стержня, поперечное сечение которого составлено из прямоугольника, швеллера и равнобокого уголка, и крыла самолёта Ту-154.

Статья в формате PDF

801 KB

стержни

изотропия

запас прочности

метод предельных состояний

1. Дарков А.В., Шпиро Г.С. Сопротивление материалов. – М.: Высш. шк., 1975. – 654 с.

2. Смирнов А.Ф., Александров А.В., Монахов Н.И. и др. Сопротивление материалов. – М.: Высш. шк., 1975. – 480 с.

3. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. – М.: Высш. шк., 1984. – 472 с.

4. Сибгатуллин К.Э., Сибгатуллин Э.С. Метод вычисления предельных сил и моментов для изотропных стержней произвольного поперечного сечения в общем случае их сложного сопротивления // Изв. вузов. Авиационная техника. – 2008. – № 2. – С. 14–16.

5. Качанов Л.М. Основы теории пластичности. – М.: Наука, 1969. – 420 с.

6. Сибгатуллин К.Э., Сибгатуллин Э.С., Тимергалиев С.Н. Прогнозирование прочности стержней, входящих в конструкцию несущей системы автомобиля КамАЗ // Изв. ТулГУ. Технические науки. – 2010. – Вып. 4. – Ч. 2. – С. 153–160.

7. Сибгатуллин К.Э., Сибгатуллин Э.С., Шибаков В.Г. Оценка предельной грузоподъемности несущей системы самосвала КамАЗ 65115 // Перспективы науки. – 2010. – № 11(13). – С. 64–73.

8. Качанов Л.М. Основы механики разрушения. – М.: Наука, 1974. – 312 с.

Во многих курсах науки о сопротивлении материалов [1, 2, 3 и др.] рассматривают, как правило, следующие частные случаи сложного сопротивления стержня: косой изгиб, внецентренное сжатие (растяжение), изгиб с кручением. Влиянием поперечных сил на разрушение стержня при его сложном сопротивлении часто пренебрегают, считая это влияние несущественным. Проверку прочности стержня осуществляют, сопоставляя наибольшее нормальное (или эквивалентное) напряжение max|σ|, действующее в опасной точке стержня, с соответствующим опасным напряжением |σu| для материала. В настоящей работе предложена методика проверки прочности изотропных стержней, при нахождении в пространстве сил и моментов. Она является развитием работы [4].

На рис. 1 показаны ВСФ, действующие в поперечном сечении стержня: 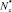– нормальная сила; 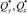– поперечные силы; 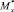– крутящий момент; 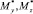– изгибающие моменты. При известном векторе ВСФ 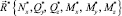необходимо определить соответствующий ему вектор прочности 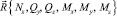и коэффициент запаса несущей способности рассматриваемого сечения

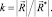(1)

На рис. 2 схематически изображена предельная поверхность (поверхность прочности) Σ в пространстве ВСФ. Здесь 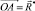– известный вектор ВСФ (например, из решения задачи о напряженно-деформированном состоянии стержня методами сопротивления материалов). 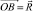– искомый вектор прочности, соответствующий вектору 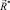. Очевидно, что векторы 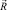и 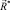должны лежать на одной прямой и быть одинаково направленными; их начала должны совпадать с началом координат в пространстве ВСФ.

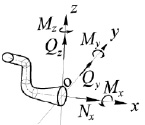
Рис. 1. ВСФ, действующие в поперечном сечении стержня

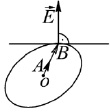
Рис. 2. Поверхность прочности Σ в пространстве ВСФ

Критерий достижения предельного состояния материала стержня запишем в следующем виде:

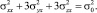(2)

Критерий (2) для стержней следует из критерия Мизеса [5], когда справедливы следующие гипотезы:

σ_yy = σ_zz = 0; ε_yz = ε_zy = 0.

Здесь σ_ij, ε_ij (i, j = x, y, z) – компоненты тензоров напряжений и деформации соответственно; σ₀ – опасное значение нормального напряжения при линейном напряженном состоянии. В работе [4], исходя из уравнения (2) и используя жесткопластическую модель деформируемого твердого тела, получили следующие параметрические уравнения предельной поверхности в пространстве ВСФ для изотропных стержней:

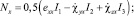
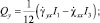
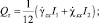
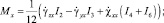(3)

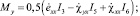
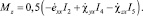
Параметрами в системе уравнений (3) являются отношения компонент вектора скоростей обобщенных перемещений 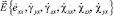. В общем случае эти параметры невозможно исключить из уравнений (3), используя для этой цели точные математические методы. В работе [4] приведены алгоритм построения различных сечений поверхности (3) и некоторые примеры построения таких сечений. Информация о сечениях поверхности (3) полезна, например, при решении задач о предельном состоянии стержневых конструкций (балок, ферм, рам) с применением кинематического и статического методов теории предельного равновесия [5] и аппарата математического программирования (см., например, работы [6, 7]). Различные сечения поверхности (3) могут быть полезными и при определении коэффициента запаса по несущей способности в частных случаях сложного сопротивления стержней. Например, имея сечения поверхности (3) координатной плоскостью NxOMx,, можно сравнивать соответствующие векторы 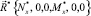и 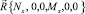при растяжении (сжатии) с кручением. Можно предположить, что область практических приложений уравнений (3) существенно расширится, если удастся использовать их при определении коэффициента запаса несущей способности в самом общем случае сложного сопротивления стержней. Ниже приведен вариант решения этой проблемы.

Компоненты коллинеарных векторов 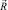и 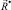удовлетворяют следующим равенствам:

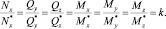(4)

Используя (4), можно записать следующую систему уравнений:

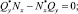
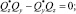
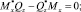(5)

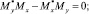
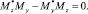
Подставив (3) в (5), получаем

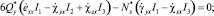
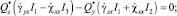
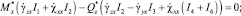(6)

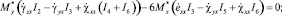
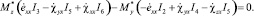
Так как в рассматриваемом случае существенное значение имеет только направление вектора 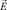, а его длина может быть произвольной, в качестве дополнительного к системе (6) примем уравнение

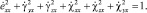(7)

Алгоритм определения коэффициента запаса по предельным состояниям изотропных стержней в общем случае их сложного сопротивления:

1. Определить вектор ВСФ 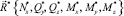в опасном сечении стержня.

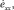
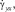
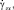
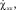
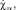
2. Решить систему уравнений (6), (7) относительно 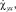т.е. найти вектор 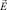, связанный с вектором прочности 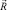ассоциированным законом [5] (рис. 2).

3. Используя формулы (3), по известному вектору 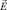определить соответствующий вектор прочности .

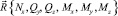4. Проверить выполнение условий (4).

5. Используя (1), определить коэффициент запаса прочности k изотропного стержня по методу предельных состояний.

Искомые компоненты вектора 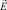присутствуют и в составе подынтегральных функций интегралов по площади поперечного сечения I1–I6 [4].

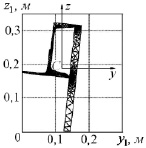
Рис. 3. Поперечное сечение составного стержня

Рассмотрим составной стержень, поперечное сечение которого показано на рис. 3. Прямоугольник имеет размеры 0,02×0,32 м, размеры швеллера соответствуют № 16, а равнобокого уголка – № 8. На рис. 3 представлен вариант разбиения сечения на конечные элементы – для численного вычисления интегралов I₁–I₆. Оси y, z – главные центральные оси сечения, y₁, z₁ – произвольные оси. Для этого стержня в работе [4] приведены некоторые сечения предельной поверхности (3).

С использованием программы, реализующей вышеописанный алгоритм, были получены результаты, приведенные в таблице. Строки 1–8 соответствуют сечению, изображённому на рис. 3; в них силы умножены на 10³, моменты – на 10⁴. Строки 9–14 соответствуют сечению, приведённому на рис. 4. Силы имеют размерность м², моменты – м³.

В качестве второго примера рассмотрим определение коэффициентов запаса прочности для сечения крыла самолёта Ту-154 при различных сочетаниях заданных внутренних сил и моментов (рис. 4). Геометрические параметры крыла приведены на сайте http://www.twirpx.com/files/transport/aircrafting/ft.blueprint/. На рис. 4 выделена учитываемая при расчётах часть профиля крыла.

Предлагаемая методика проверки прочности стержней имеет следующие достоинства:

1. Исчезает необходимость выделения частных видов сложного сопротивления стержней (косой изгиб, изгиб с кручением и т.п.).

2. Все компоненты ВСФ, действующие в поперечном сечении стержня, на равных правах участвуют в процессе проверки прочности.

3. На форму и размеры стержня накладываются только самые общие ограничения, принятые в теории стержней.

4. Метод проверки прочности по предельным состояниям позволяет точнее определять коэффициент запаса прочности, чем метод расчета по допускаемым напряжениям – особенно в тех случаях, когда имеет место вязкое разрушение. В работе [8] отмечено: «Очевидно, что расчет по предельным нагрузкам дает существенно более правильное представление о прочности конструкции, чем расчет по максимальным напряжениям». Это утверждение справедливо и для отдельно взятых стержней.

Предлагаемая методика проверки прочности стержней по предельным состояниям может найти применение в практике расчетов и проектирования различных изделий.

Некоторые результаты определения k

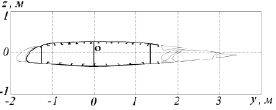
Рис. 4. Поперечное сечение крыла самолёта Ту-154

Рецензенты:

Габбасов Н.С., д.ф.-м.н., профессор, заведующий кафедрой математики, Набережночелнинский институт (филиал), Казанский (Приволжский) федеральный университет, г. Набережные Челны;

Хабибуллин Р.Г., д.т.н., профессор, заведующий кафедрой сервиса транспортных систем, Набережночелнинский институт (филиал), Казанский (Приволжский) федеральный университет, г. Набережные Челны.

Библиографическая ссылка