Сопоставление результатов, изложенных в предыдущих сообщениях [3, 4], указывает на существование связей между показателями ряда свойств меловальной суспензии и мелованной бумаги, что проявляется в корреляциях между наблюдаемыми переменными (свойствами) Y1, Y2, …, Ym, включенными в исследование. Наличие корреляций является следствием существования нескольких (меньше, чем число переменных m) «латентных» факторов, изменение которых под влиянием условий (состава меловальной суспензии) вносит совместный вклад в варьирование реологических и бумагомодифицирующих свойств суспензии. Для анализа структуры связей между переменными используются методы многомерного факторного анализа [1, 5].
Дисперсии и корреляции нормализованных переменных Y1, Y2, …, Ym образуют m×m матрицу С = {cij} с дисперсиями на главной диагонали (при i = j) и корреляциями вне главной диагонали (при i ¹ j). Задача факторного анализа заключается в построении математической модели в виде линейной регрессии
Yi = li1f1 + li2f2 + … + litft + εi; i = 1, …, m; m > t (1)
на основании информации, заключенной в корреляционной матрице С. В выражении (1) переменные fj – латентные факторы; коэффициенты lij – нагрузки j-го фактора в i-й переменной. Слагаемые εi – остатки с дисперсиями vi, представляющие собой источники отклонений, действующие только на Yi. Факторная модель (1) содержит в себе следующую основную гипотезу факторного анализа: множество коррелированных переменных Yi (i = 1, 2, …, m) можно описать меньшим числом латентных факторов fj (j = 1, 2, …, t; m > t) и множеством независимых остатков εi (i = 1, …, m).
Из выражения (1) следует, что корреляционная (в общем случае ковариационная) матрица может быть выражена через нагрузки и остаточные дисперсии:
C = LLТ + V, (2)
где L – матрица m×t факторных нагрузок lij; V – диагональная матрица m×m c остаточными дисперсиями vi на диагонали.
При умножении L в выражении (2) на любую ортогональную матрицу размера t×t произведение LLТ не изменяется. Следствием этого является существование бесчисленного множества решений, удовлетворяющих равенству (2) и равноценных по статистическим критериям. Поиск наилучшей модели (1) проводят в два этапа. Вначале находят частное решение, удовлетворяющее какому-либо дополнительному формальному ограничению, однозначно фиксирующему факторные нагрузки. Затем производят ортогональное преобразование L («вращение» пространства факторов), при котором латентные факторы приобретают физическую содержательность.
Экспериментальная часть
Исследовали меловальную суспензию со следующим соотношением компонентов (по массе): пигменты 84,0 %, связующие 14,4 %, глицерин 0,7 %, Na-полифосфат 0,9 %. В качестве пигментов использовали каолин, тальк, мел и их смеси. Массовую долю каждого из пигментов в их смеси варьировали в диапазоне значений от 0 до 1 согласно симплекс-центроидному плану эксперимента (7 уровней) [2, 6]. В качестве связующих использовали натриевую соль карбоксиметилцеллюлозы (далее КМЦ), бутадиенстирольный латекс (БДС), поливинилацетатный латекс (ПВА) и их смеси. Массовую долю (по сухому веществу) каждого из связующих в их смеси варьировали также от 0 до 1 с использованием симплекс-центроидного плана (7 уровней). Меловальные составы наносили на бумагу с помощью лабораторного шаберного устройства. Свойства суспензии и мелованной бумаги характеризовали следующими показателями:
Y1 – эффективная вязкость меловальной суспензии, Па·с;
Y2 – индекс течения (степень аномальности течения);
Y3 – эффективная энергия активации течения суспензии, кДж/моль;
Y4 – условная вязкость суспензии, с;
Y5 – водоудерживающая способность суспензии;
Y6 – плотность мелованной бумаги, г/см3;
Y7 – масса наноса покрытия, г/м2;
Y8 – сопротивление бумаги разрыву;
Y9 – воздухопроницаемость мелованной бумаги, см3/мин;
Y10 – смачиваемость покрытия, г/м2;
Y11 – жесткость бумаги, единицы градуировки прибора.
Кроме того, для облегчения интерпретации результатов факторного анализа в число свойств включены переменные, характеризующие составы меловальных суспензий:
Y12, Y13, Y14 – массовые доли соответственно каолина, талька и мела в составе пигмента;
Y15, Y16, Y17 – массовые доли соответственно КМЦ, БДС и ПВА в составе связующего.
Методы определения и статистические характеристики свойств Y1 ... Y11 приведены в нашем предыдущем сообщении [4]. Объем выборки составил 49 наблюдений (объектов). Для статистической обработки (корреляционного и факторного анализов) использован пакет прикладных программ Statistica v.10.
Результаты исследования и их обсуждение
Элементы матрицы парных линейных корреляций С между переменными Y1 ... Y11 приведены в табл. 1 (верхняя половина над главной диагональю).
Три первых – собственные числа EV матрицы корреляций больше 1, они приведены в табл. 2. Следовательно, для анализа структуры корреляционных связей между изучаемыми свойствами (объектами) имеет смысл привлечь три латентных фактора, ответственных за 65,6 % суммарной дисперсии переменных. Факторные нагрузки lij (табл. 3) вычислили методом итеративных общностей minres, для ортогонального преобразования использовали критерий varimax, при котором вращение пространства латентных факторов осуществляется с таким расчетом, чтобы наибольшее число элементов в столбцах матрицы нагрузок оказалось близким к 0 или 1 (по абсолютной величине). Элементы главной диагонали матрицы корреляций (табл. 1) соответствуют остаточным дисперсиям переменных (за вычетом долей, обусловленных влиянием латентных факторов), ниже диагонали помещены остаточные корреляции между переменными.
Наглядное представление о связи наблюдаемых переменных с латентными факторами дает рисунок – проекции точек с координатами из табл. 3 на двумерные грани трехмерной области факторного пространства.
Таблица 1
Элементы матриц корреляций между Y1 ... Y11 (над главной диагональю; критическое значение ±0,28 при уровне значимости 0,05), остаточных дисперсий (на диагонали) и остаточных корреляций (под диагональю)
|
Переменные |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
Y8 |
Y9 |
Y10 |
Y11 |
|
Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 |
0,10 –0,08 0,05 0,03 –0,07 0,00 0,04 0,08 0,04 –0,03 –0,05 |
0,01 0,72 –0,03 –0,01 0,08 0,11 –0,24 0,11 –0,16 –0,12 0,21 |
0,66 0,02 0,46 0,03 0,03 –0,04 0,14 0,02 –0,08 –0,19 –0,13 |
0,77 –0,16 0,37 0,19 –0,04 –0,02 0,11 –0,05 0,01 –0,02 –0,15 |
0,12 –0,29 –0,12 0,47 0,36 –0,08 0,11 –0,06 0,25 0,08 –0,13 |
–0,40 –0,35 –0,60 0,01 0,46 0,16 –0,10 –0,06 –0,05 –0,02 0,02 |
–0,77 –0,37 –0,44 –0,51 0,00 0,33 0,27 –0,15 0,18 0,08 –0,23 |
–0,42 –0,15 –0,46 –0,28 0,04 0,49 0,33 0,56 –0,08 –0,02 0,18 |
0,09 –0,16 0,03 –0,06 0,08 –0,26 0,12 –0,20 0,94 0,35 –0,30 |
0,64 0,00 0,32 0,47 0,11 –0,44 –0,54 –0,45 0,42 0,47 –0,19 |
0,66 0,22 0,30 0,50 0,13 –0,18 –0,85 –0,16 –0,30 0,33 0,42 |
Таблица 2
Собственные числа (EV – Eigenvalue) матрицы корреляций
|
Номер EV |
Величина EV |
Доля общей дисперсии, % |
Кумулятивные EV |
Кумулятивные дисперсии, % |
|
1 2 3 |
5,754 2,843 2,554 |
33,85 16,72 15,03 |
5,754 8,597 11,151 |
33,85 50,57 65,60 |
Таблица 3
Нагрузки lij латентных факторов fj в переменных Yi
|
Переменные |
Факторы fj |
||
|
f1 |
f2 |
f3 |
|
|
нагрузки факторов lij |
|||
|
Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 Y12 Y13 Y14 Y15 Y16 Y17 |
0,932 0,157 0,677 0,683 0,075 –0,568 –0,836 –0,569 0,171 0,772 0,685 0,077 –0,071 –0,006 0,685 –0,954 0,268 |
0,113 0,026 0,027 0,288 0,232 0,368 –0,296 0,228 –0,855 –0,361 0,548 0,817 –0,286 –0,529 –0,302 –0,052 0,355 |
0,053 –0,747 –0,215 0,389 0,642 0,493 0,136 0,189 0,272 0,253 –0,017 0,227 –0,241 0,014 0,523 0,220 –0,741 |
Наибольшие нагрузки первого латентного фактора приходятся на переменные Y1, Y3 и Y4, характеризующие вязкость меловальной суспензии, а также на переменные Y15 и Y16. Поскольку увеличение доли КMЦ в связующем сопровождается наибольшим повышением вязкости суспензии, а введение БДС, напротив, резко снижает вязкость [3], логично интерпретировать природу первого фактора как соотношение этих двух компонентов в составе связующего. С такой интерпретацией согласуются также большие положительные нагрузки первого фактора на переменные Y10 и Y11 и отрицательная – на Y7.
Второй фактор однозначно интерпретирован как доля каолина в составе пигмента. На это указывает его высокая положительная нагрузка в переменной Y12 и отрицательная – в переменной Y9. Известно, что каолин в покрытии уменьшает воздухопроницаемость мелованной бумаги в значительно большей степени, чем тальк и мел [3, 7].
Природа третьего фактора связана с долей ПВА в составе связующего (переменная Y17), наиболее существенно его влияние отразилось на степени аномальности течения (переменная Y2) и водоудерживающей способности (переменная Y5) суспензии.
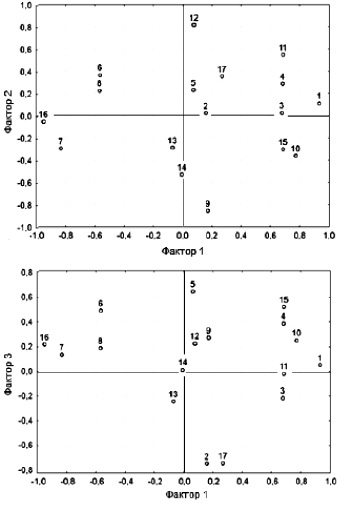
Связь объектов наблюдений с латентными факторами (числа у точек – индексы i переменных Yi)
Заключение
Факторный анализ можно рассматривать в определенном смысле как один из способов группировки свойств изучаемых объектов по характеру их связи с гипотетическими «латентными факторами». Во многих случаях результаты такой группировки не противоречат результатам кластеризации свойств [4]. Некоторые различия обусловлены принципиально разными механизмами классификации: кластерный анализ оперирует многомерными «геометрическими расстояниями» между свойствами, а факторный – корреляционными связями между ними. Оба способа исследования взаимно дополняют друг друга.
Рецензенты:
Алашкевич Ю.Д., д.т.н., профессор, заведующий кафедрой «Машины и аппараты промышленных технологий», ФГБОУ ВО «Сибирский государственный технологический университет», г. Красноярск;
Доррер Г.А., д.т.н., профессор, заведующий кафедрой «Системотехника», ФГБОУ ВО «Сибирский государственный технологический университет», г. Красноярск.



