При изучении реологических и бумагомодифицирующих свойств меловальных суспензий сложного многокомпонентного состава объекты исследования (суспензию, мелованную бумагу) характеризовали большим числом непосредственно измеряемых показателей [5, 10]. При этом возникает естественный вопрос: возможно ли объединение некоторых показателей в группы, характеризующие одно и то же физическое свойство объекта, но измеренное разными способами? Ответ может быть получен методами классификации, к числу которых относится кластерный анализ [1, 2, 7]. В случае успеха это позволило бы сократить число ограничений при формулировании и решении оптимизационных задач методами математического программирования. Кроме того, такая постановка вопроса интересна и в познавательном плане.
Экспериментальная часть
Исследованиям подвергали меловальную суспензию со следующим соотношением компонентов (по массе): пигменты 84 %, связующие 14,4 %, глицерин 0,7 %, Na-полифосфат 0,9 %. В качестве пигментов использовали каолин, тальк, мел и их смеси. Массовую долю каждого из пигментов в их смеси варьировали в диапазоне значений от 0 до 1 согласно симплекс-центроидному плану эксперимента (7 уровней) [3, 8]. В качестве связующих использовали натриевую соль карбоксиметилцеллюлозы, бутадиенстирольный латекс, поливинилацетатный латекс и их смеси. Массовую долю (по сухому веществу) каждого из связующих в их смеси варьировали также от 0 до 1 с использованием симплекс-центроидного плана (7 уровней). Меловальные составы наносили на бумагу с помощью лабораторного шаберного устройства. Свойства объектов (суспензии и мелованной бумаги) характеризовали следующими показателями:
Y1 – эффективная вязкость меловальной суспензии, Па·с;
Y2 – индекс течения (степень аномальности течения);
Y3 – эффективная энергия активации течения суспензии, кДж/моль;
Y4 – условная вязкость суспензии, с;
Y5 – водоудерживающая способность суспензии;
Y6 – плотность мелованной бумаги, г/см3;
Y7 – масса наноса покрытия, г/м2;
Y8 – изменение сопротивления бумаги разрыву;
Y9 – воздухопроницаемость мелованной бумаги, см3/мин;
Y10 – смачиваемость покрытия, г/м2;
Y11 – жесткость бумаги, единицы градуировки прибора.
Индекс течения суспензии определяли по кривым течения [4]. Условную вязкость измеряли с помощью вискозиметра В3-4 и характеризовали продолжительностью вытекания 100 см3 суспензии через отверстие диаметром 4 мм. Методы определения остальных показателей приведены в [6].
Объем выборки составил 49 наблюдений. Для статистической обработки (дескриптивный, кластерный и дискриминантный анализы) использован пакет прикладных программ Statistica v.10.
Статистические характеристики свойств Y1...Y11 приведены в табл. 1.
Таблица 1
Статистические характеристики переменных Y1...Y11 (объем выборки N = 49)
|
Переменные |
Среднее |
Минимум |
Максимум |
Дисперсия |
Коэффициент вариации, % |
|
Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 |
0,875 0,528 46,5 12,8 0,362 0,735 28,6 1,23 22,9 31,3 60,4 |
0,007 0,384 12,9 4,50 0,220 0,690 14,0 1,08 2,90 11,0 49,3 |
2,11 0,658 83,4 65,0 1,00 0,803 58,2 1,45 62,0 52,8 75,5 |
0,4012 0,0037 241,6 106,3 0,0128 0,0007 105,9 0,0055 289,4 94,21 35,19 |
72,4 11,6 33,4 80,6 31,3 3,70 36,0 6,04 74,1 31,0 9,83 |
Кластерный анализ выполнен методом Варда (Ward’s method) с использованием нормализованных значений переменных (свойств) и квадрата «евклидова расстояния» (Squared Euclidean distance) в качестве метрики.
Результаты исследования и их обсуждение
На рисунке приведена дендрограмма классификации всех 11 свойств Y1...Y11. Числа на оси абсцисс соответствуют индексам свойств.
На основании визуальной оценки можно сформулировать гипотезу о возможности группировки свойств по величине «расстояний» между ними в три кластера A, B и С. В кластер А входят свойства Y1, Y3, Y4, Y11; в кластер В – свойства Y2, Y9, Y10; в кластер С – свойства Y5, Y6, Y7, Y8.
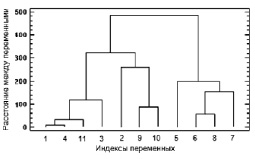
Дендрограмма классификации свойств Y; числа на оси абсцисс соответствуют подстрочным индексам в обозначении свойств
Таблица 2
Статистические характеристики дискриминантных функций
|
Дискриминантные функции |
Собственные числа, EV |
Доли EV, % |
Лямбда Уилкса, λ |
χ2 |
р – уровни значимости |
|
1 2 |
40,22 1,71 |
95,92 4,08 |
0,0089 0,369 |
58,96 12,47 |
0,0000 0,0059 |
Кластерный анализ позволяет разделить выборку на группы (кластеры) по принципу «геометрической близости» свойств, однако не дает ни правил, ни статистических критериев оценки качества классификации. Для проверки гипотезы выполнен дискриминантный анализ [1, 7], в котором принадлежность свойств к одному из кластеров А, В или С служит категориальной (группирующей) переменной. Максимальное число дискриминантных функций равно двум (на единицу меньше числа кластеров). Их статистические характеристики приведены в табл. 2.
Основной «вес» в дискриминации приходится на первую дискриминантную функцию, доля её собственного числа EV (Eigenvalue) в сумме собственных чисел обеих функций составляет почти 96 %. Близкая к нулю величина критерия λ, большая величина критерия χ2 и низкий уровень значимости р (меньше 0,05) указывают на высокую достоверность результатов классификации свойств. Это же подтверждается 100 %-ным совпадением результатов дискриминантного и кластерного анализов (табл. 3).
Объединение в кластере А показателей Y1, Y3 и Y4 естественно – все три свойства характеризуют вязкость меловальной суспензии. При шаберном способе нанесения покрытия уменьшение вязкости (при прочих одинаковых условиях) сопровождается увеличением массы наноса, что, в свою очередь, приводит к снижению жесткости бумаги Y11 [9, 11]. Между всеми четырьмя показателями существуют обусловленные этим статистически значимые положительные корреляции, поэтому свойство Y11 также оказалось отнесенным к кластеру А.
Принадлежность показателей воздухопроницаемости Y9 и смачиваемости Y10 бумаги к одному кластеру В объясняется их положительными корреляционными связями с массовыми долями мела в составе пигмента и Na-карбоксиметилцеллюлозы в составе связующего. Эти особенности названных компонентов меловальных суспензий известны и используются для управления промышленными процессами мелования [9, 11]. Отнесение характеристики аномальности течения суспензии Y2 к кластеру В также обусловлено её связью с особенностями реологических свойств растворов КМЦ [10].
Между переменными, образовавшими кластер С, существуют положительные корреляционные связи. Не останавливаясь на теоретических предпосылках этого явления (они обсуждались в предыдущем сообщении [6]), отметим лишь, что результаты наблюдений согласуются с имеющейся априорной информацией [5, 9, 10, 11].
Таблица 3
Результаты классификации свойств
|
Объекты, Yu |
Отнесение свойств |
||
|
кластерный анализ |
дискриминантный анализ |
||
|
кластеры |
вероятность отнесения |
||
|
Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 |
А В А А С С С С В В А |
А В А А С С С С В В А |
1,000 1,000 0,998 0,995 0,999 1,000 0,997 1,000 0,993 0,996 0,987 |
Заключение
Классификационный анализ свойств 49 объектов наблюдения (образцов меловальной суспензии и мелованной бумаги) позволил произвести свертку 11-мерного пространства измеренных свойств объектов до 3-мерного пространства «кластерных свойств» этих объектов. Этот результат может быть полезен для обсуждения проблем квалиметрии при выборе параметров оптимизации и критериев оптимальности технологических процессов мелования бумаги.
Рецензенты:
Алашкевич Ю.Д., д.т.н., профессор, заведующий кафедрой «Машины и аппараты промышленных технологий», ФГБОУ ВО «Сибирский государственный технологический университет» Министерства образования и науки РФ, г. Красноярск;
Доррер Г.А., д.т.н.., профессор, заведующий кафедрой «Системотехника», ФГБОУ ВО «Сибирский государственный технологический университет» Министерства образования и науки РФ, г. Красноярск.



