Коинтегрированность является важным свойством многих экономических переменных, которое означает, что несмотря на стохастический характер изменения отдельных экономических переменных, существует долгосрочная зависимость между ними, которая приводит к некоторому совместному, взаимосвязанному изменению, когда краткосрочные изменения корректируются в зависимости от степени отклонения от долгосрочной зависимости. Такое поведение присуще коинтегрированным временным рядам.
Для реализации метода коинтеграционного анализа необходимо ввести понятие коинтегрированных временных рядов. Интегрированным временным рядом называется нестационарный временной ряд, разности некоторого порядка которого являются стационарным временным рядом. Примером интегрированного временного ряда является случайное блуждание, часто используемое при моделировании финансовых временных рядов. Если стационарностью обладает ряд, составленный из первых разностей, то его принято называть интегрированным рядом первого порядка (обозначается I(1)).
Рассмотрим два временных ряда интегрированных первого порядка yt ~ I(1) и xt ~ I(1). Если ряд yt – bxt ~ I(0) представляет собой стационарный ряд при b ≠ 0, то ряды xt и yt называют коинтегрированными, а вектор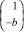 
– коинтегрирующим вектором.
В общем случае ряды yt ~ I(1), xt ~ I(1) называют коинтегрированными, если существует ненулевой вектор β = (β1, β2)T ≠ 0, для которого β1xt + β2yt ~ I(0) – стационарный ряд.
Важно отметить, что если вектор β = (β1, β2)T является коинтегрирующим для рядов xt и yt, то коинтегрирующим для этих рядов будет и любой вектор вида cβ = (cβ1, cβ2)T, где c ≠ 0 – постоянная величина. Поэтому чтобы выделить какой-то определенный вектор, необходимо вводить условие нормировки.
Если максимальное количество линейно независимых коинтегрирующих векторов для заданных N рядов равно r, то это число r называется рангом коинтеграции (cointegration rank).
Совокупность всех возможных коинтегрирующих векторов для коинтегрированной системы I(1) рядов образует r-мерное линейное векторное пространство, которое называют коинтеграционным пространством. Любой набор r линейно независимых коинтегрирующих векторов образует базис этого пространства, и, если зафиксировать этот набор в качестве базиса, то любой коинтегрирующий вектор является линейной комбинацией векторов, составляющей базис.
При наличии нескольких коинтегрирующих векторов возникает проблема идентификации каждого из них. Каждый такой вектор должен выражать осмысленные с точки зрения экономической теории долговременные зависимости между рассматриваемыми переменными. Применение идентифицирующих ограничений позволяет различать векторы.
Оценивание ранга коинтеграции и последующее построение модели коррекции ошибок производится при помощи теста Йохансена.
Рассматривается модель векторной авторегрессии [1], построенной на N интегрированных рядах первого порядка вида yt ~ I(1), i = 1, ..., N:
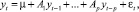
где A1, ..., Ap – матрицы размера (N×N).
Путем алгебраических преобразований эту модель также можно представить в виде
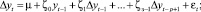
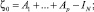
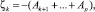k = 1, 2, ..., p – 1.
Ранг матрицы ζ0 обычно и называют рангом коинтеграции рассматриваемой системы рядов. В общем случае он может принимать значения от 0 до N:
● значения r = 1, …, N – 1 соответствуют коинтегрированной векторной авторегрессии;
● если r = 0, то ряды y1t, …, yNt не коинтегрированы;
● если r = N, то ряды y1t, …, yNt, то любой N-мерный вектор является коинтегрирующим. Это означает, что все изучаемые ряды являются стационарными.
Прежде чем применять процедуру теста Йохансена, следует определиться с порядком p-векторной авторегрессии, которой следует векторный ряд [2, 3, 4].
В процессе оценивания ранга коинтеграции возникают две проблемы. Первая заключается в том, что заранее обычно не известно, на какое значение r следует рассчитывать. Йохансен предложил последовательную процедуру проверки гипотез, с помощью которой можно получить состоятельную оценку истинного ранга коинтеграции.
Процедура состоит в последовательных проверках гипотез о равенстве ранга коинтеграции H0: r = i, i = 0, ..., N против альтернативной гипотезы H0: r = i + 1 при 0,05 уровне значимости.
Вторая проблема связана с тем, что критические значения статистик критериев отношения правдоподобия зависят не только от r* и N, но и от того, имеют ли ряды детерминированные тренды, включается ли константа и/или тренд в коинтеграционное отношение (cointegration equation – CE). Для проверки всех ситуаций для всех возможных значений r применяют информационные критерии Акаике и Шварца. Наилучшая модель выбирается по наименьшим значениям этих критериев.
При использовании критерия Акаике для нормальной линейной модели с p объясняющими переменными, оцененной по n наблюдениям, сопоставляется значение
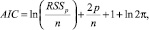
где RSSp – остаточная сумма квадратов, полученная при оценивании коэффициентов модели методом наименьших квадратов.
При увеличении количества объясняющих переменных первое слагаемое в правой части уменьшается, а второе – увеличивается. Среди нескольких альтернативных предпочтение отдается модели с минимальным AIC, в которой достигается определенный компромисс между величиной остаточной суммы квадратов и количеством объясняющих переменных.
Информационный критерий Шварца основан на следующей статистике:
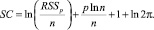
Здесь также при увеличении количества объясняющих переменных первое слагаемое увеличивается, а второе – уменьшается. И также предпочтение отдается модели с наименьшим показателем SC.
В общем случае не обязательно, что оба критерия выберут одну и ту же модель. Причиной тому является определенная специфика каждого критерия. Так, критерий Шварца является состоятельным в следующем смысле: если среди альтернативных моделей есть модель, соответствующая истинному процессу порождения данных, то при неограниченном увеличении количества наблюдений применение критерия Шварца выводит именно на эту модель. Критерий Акаике с такой точки зрения выводит на более полную модель. Исходя из принципа экономичности, предпочтительнее использовать критерий Шварца. Однако в некоторых случаях, когда критерий Акакике останавливается на более полной модели по сравнению с моделью, выбранной критерием Шварца, исследователи все же оставляют для дальнейшего рассмотрения и модель, выбранную критерием Акаике. Это в основном зависит от целей, которые перед собой ставит исследователь.
В нашем случае для нахождения ранга коинтеграции для ВВП России, Белоруссии и Казахстана следует провести предварительный анализ отобранных рядов. Статистические данные собраны из открытых интернет-источников. В первую очередь необходимо убедиться, что изучаемые ряды представляют собой интегрированные ряды первого порядка.
Для этого при помощи процедуры Tramo/Seats в специализированном эконометрическом пакете Eviews для каждого из рядов была проведена декомпозиция. По её результатам во всех данных был обнаружен тренд (рисунок), что говорит о том, что ряды являются нестационарными.
На следующем шаге при помощи теста Дики – Фуллера и KPSS-теста на единичный корень осуществлялась проверка стационарности первой разницы. Результаты приведены в табл. 1.
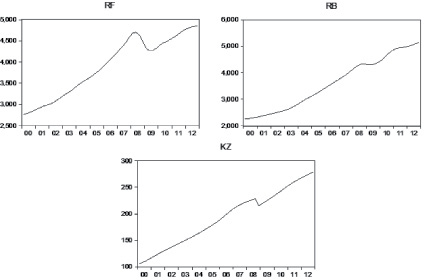
Тренды в данных России, Белоруссии и Казахстана. Источник: [5]
Таблица 1
Результаты тестирования
|
Дики – Фуллера |
|||
|
Данные |
Россия |
Белоруссия |
Казахстан |
|
P – value |
0,0705 |
0,278 |
0,2295 |
|
KPSS-тест |
|||
|
Данные |
Россия |
Белоруссия |
Казахстан |
|
P – value |
0,19 |
0,108 |
0,105 |
Таблица 2
G-причинность
|
RF |
RB |
KZ |
|
|
RF не является G-причиной для |
– |
0,7977 |
0,1184 |
|
RB не является G-причиной для |
0,5648 |
– |
0,0013 |
|
KZ не является G-причиной для |
0,2002 |
0,366 |
– |
В качестве нулевой гипотезы здесь выступает стационарность изучаемых данных. В связи с этим первая разность стационарна, и можно заключить, что статистика ВВП выбранных стран представляет интегрированный ряд первого порядка.
Помимо проверки стационарности, отобранные ряды также стоит проверить на наличие причинности по Гренджеру.
Полученные результаты позволяют сделать вывод о G-причинности показателя ВВП Белоруссии относительно показателя ВВП Казахстана. При определенной доле допущения можно также отметить наличие G-причинности данных по России относительно данных по Казахстану. Для показателей ВВП России, Казахстана и Белоруссии имеет место следующее свойство: несмотря на случайный (слабо предсказуемый) характер изменения отдельных переменных, существует долгосрочная зависимость между ними, которая приводит к некоторому совместному, взаимосвязанному изменению.
Коинтеграционное соотношение может быть записано в форме линейного уравнения
RFt = 0,714∙RBt + 47,298∙KZt – 163,676∙trend + 3421,339.
Данное соотношение позволяет обоснованно заключить, что между ВВП изучаемых стран существует долговременное соотношение, позволяющее количественно оценивать степень взаимовлияния одной экономики на другую. Так, увеличение ВВП Казахстана на 1 млрд долл. в силу существующих экономических связей между странами приведет к увеличению ВВП Российской Федерации на 47,3 млрд долл., в то время как влияние экономики Беларуси на экономику России существенно ниже. Рост ВВП Беларуси приводит к росту ВВП России, но меньшими темпами (коэффициент меньше единицы).
В результате проведенного исследования были рассмотрены теоретические аспекты интеграции на уровне Евразийского экономического сообщества, описаны теоретические аспекты метода коинтеграционного анализа и критериев его применимости, получено коинтеграционное соотношение, показывающее степень взаимного влияния экономик стран Беларуси, России и Казахстана, которое может быть применено для дальнейшего детального исследования краткосрочной динамики интеграционных процессов изучаемых экономик.
Рецензенты:
Бабешко Л.О., д.э.н., профессор, кафедра «Системный анализ и моделирование экономических процессов», ФГБОУ ВПО «Финансовый университет при Правительстве Российской Федерации», г. Москва;
Попов В.Ю., д.ф.-м.н., профессор, руководитель департамента математики и информатики, ФГБОУ ВПО «Финансовый университет при Правительстве Российской Федерации», г. Москва.